Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-28T20:49:55.621Z Has data issue: false hasContentIssue false
  • English
  • Français

Surfactant and gravity dependent instability of two-layer Couette flows and its nonlinear saturation

Published online by Cambridge University Press:  03 August 2017

Alexander L. Frenkel  and
David Halpern Open the ORCID record for David Halpern [Opens in a new window]
Alexander L. Frenkel
Affiliation:
Department of Mathematics, University of Alabama, Tuscaloosa, AL 35487, USA
David Halpern*
Affiliation:
Department of Mathematics, University of Alabama, Tuscaloosa, AL 35487, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A horizontal channel flow of two immiscible fluid layers with different densities, viscosities and thicknesses, subject to vertical gravitational forces and with an insoluble surfactant monolayer present at the interface, is investigated. The base Couette flow is driven by the uniform horizontal motion of the channel walls. Linear and nonlinear stages of the (inertialess) surfactant and gravity dependent long-wave instability are studied using the lubrication approximation, which leads to a system of coupled nonlinear evolution equations for the interface and surfactant disturbances. The (inertialess) instability is a combined result of the surfactant action characterized by the Marangoni number 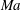$Ma$ and the gravitational effect corresponding to the Bond number 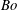$Bo$ that ranges from 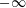$-\infty$ to 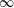$\infty$. The other parameters are the top-to-bottom thickness ratio $n$, which is restricted to 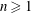$n\geqslant 1$ by a reference frame choice, the top-to-bottom viscosity ratio 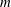$m$ and the base shear rate $s$. The linear stability is determined by an eigenvalue problem for the normal modes, where the complex eigenvalues (determining growth rates and phase velocities) and eigenfunctions (the amplitudes of disturbances of the interface, surfactant, velocities and pressures) are found analytically by using the smallness of the wavenumber. For each wavenumber, there are two active normal modes, called the surfactant and the robust modes. The robust mode is unstable when 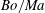$Bo/Ma$ falls below a certain value dependent on 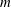$m$ and $n$. The surfactant branch has instability for 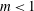$m<1$, and any 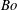$Bo$, although the range of unstable wavenumbers decreases as the stabilizing effect of gravity represented by 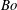$Bo$ increases. Thus, for certain parametric ranges, even arbitrarily strong gravity cannot completely stabilize the flow. The correlations of vorticity-thickness phase differences with instability, present when gravitational effects are neglected, are found to break down when gravity is important. The physical mechanisms of instability for the two modes are explained with vorticity playing no role in them. This is in marked contrast to the dynamical role of vorticity in the mechanism of the well-known Yih instability due to effects of inertia, and is contrary to some earlier literature. Unlike the semi-infinite case that we previously studied, a small-amplitude saturation of the surfactant instability is possible in the absence of gravity. For certain 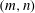$(m,n)$-ranges, the interface deflection is governed by a decoupled Kuramoto–Sivashinsky equation, which provides a source term for a linear convection–diffusion equation governing the surfactant concentration. When the diffusion term is negligible, this surfactant equation has an analytic solution which is consistent with the full numerics. Just like the interface, the surfactant wave is chaotic, but the ratio of the two waves turns out to be constant.

JFM classification

Low-Reynolds-number flows: Lubrication theory Multiphase and Particle-laden Flows: Multiphase flow Instability: Nonlinear instability
Type
Papers
Information
Journal of Fluid Mechanics , Volume 826 , 10 September 2017 , pp. 158 - 204
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Babchin, A. J., Frenkel, A. L., Levich, B. G. & Sivashinsky, G. I. 1983 Nonlinear saturation of Rayleigh–Taylor instability in thin films. Phys. Fluids 26, 3159–3161.Google Scholar
Barthelet, P., Charru, F. & Fabre, J. 1995 Experimental study of interfacial long waves in a two-layer shear-flow. J. Fluid Mech. 303, 23–53.CrossRefGoogle Scholar
Bassom, A. P., Blyth, M. G. & Papageorgiou, D. T. 2010 Nonlinear development of two-layer Couette–Poiseuille flow in the presence of surfactant. Phys. Fluids 22 (10), 102102.CrossRefGoogle Scholar
Blyth, M. G. & Pozrikidis, C. 2004a Effect of inertia on the Marangoni instability of two-layer channel flow. Part II: normal-mode analysis. J. Engng Maths 50 (2–3), 329–341.Google Scholar
Blyth, M. G. & Pozrikidis, C. 2004b Effect of surfactants on the stability of two-layer channel flow. J. Fluid Mech. 505, 59–86.Google Scholar
Chandrasekhar, C. 1961 Hydrodynamics and Hydromagnetic Stability. Dover.Google Scholar
Charru, F. & Hinch, E. J. 2000 ‘Phase diagram’ of interfacial instabilities in a two-layer Couette flow and mechanism of the long-wave instability. J. Fluid Mech. 414, 195–223.Google Scholar
Craster, R. V. & Matar, O. K. 2009 Dynamics and stability of thin liquid films. Rev. Mod. Phys. 81 (3), 1131–1198.Google Scholar
Edwards, D. A., Brenner, H. & Wasan, D. T. 1991 Interfacial Transport Processes and Rheology. Butterworth-Heinemann.Google Scholar
Frenkel, A. L. & Halpern, D. 2000 On saturation of Rayleigh–Taylor instability. In IUTAM Symposium on Nonlinear Waves in Multi-Phase Flow, pp. 69–79. Springer.Google Scholar
Frenkel, A. L. & Halpern, D. 2002 Stokes-flow instability due to interfacial surfactant. Phys. Fluids 14 (7), L45–L48.Google Scholar
Frenkel, A. L. & Halpern, D. 2005 Effect of inertia on the insoluble-surfactant instability of a shear flow. Phys. Rev. E 71 (1), 016302.Google Scholar
Frenkel, A. L. & Halpern, D. 2006 Strongly nonlinear nature of interfacial-surfactant instability of Couette flow. Intl J. Pure Appl. Maths 29 (2), 205–224.Google Scholar
Frenkel, A. L. & Halpern, D.2016 Surfactant and gravity dependent inertialess instability of two-layer Couette flows and its nonlinear saturation. arXiv:1610.04909.Google Scholar
Gao, P. & Lu, X.-Y. 2007 Effect of surfactants on the inertialess instability of a two-layer film flow. J. Fluid Mech. 591, 495–507.CrossRefGoogle Scholar
Halpern, D. & Frenkel, A. L. 2003 Destabilization of a creeping flow by interfacial surfactant: linear theory extended to all wavenumbers. J. Fluid Mech. 485, 191–220.Google Scholar
Halpern, D. & Frenkel, A. L. 2008 Nonlinear evolution, travelling waves, and secondary instability of sheared-film flows with insoluble surfactants. J. Fluid Mech. 594, 125–156.Google Scholar
Hindmarsh, A. C., Brown, P. N., Grant, K. E., Lee, S. L., Serban, R., Shumaker, D. E. & Woodward, C. S. 2005 SUNDIALS: suite of nonlinear and differential/algebraic equation solvers. ACM Trans. Math. Softw. (TOMS) 31 (3), 363–396.Google Scholar
Hirasaki, G. & Zhang, D. L. 2004 Surface chemistry of oil recovery from fractured, oil-wet, carbonate formations. SPE J. 9, 151–1162.Google Scholar
Hooper, A. P. & Grimshaw, R. 1985 Nonlinear instability at the interface between two viscous fluids. Phys. Fluids 28, 37–45.Google Scholar
Joseph, D. D. & Renardy, Y. 1993 Fundamentals of Two-Fluid Dynamics, Vol I: Mathematical Theory and Applications; Vol II: Lubricated Transport, Drops and Miscible Liquids. Springer.Google Scholar
Kalogirou, A. & Papageorgiou, D. T. 2016 Nonlinear dynamics of surfactant-laden two-fluid Couette flows in the presence of inertia. J. Fluid Mech. 802, 5–36.Google Scholar
Kalogirou, A., Papageorgiou, D. T. & Smyrlis, Y. S. 2012 Surfactant destabilization and non-linear phenomena in two-fluid shear flows at small Reynolds numbers. IMA J. Appl. Maths 77 (3), 351–360.Google Scholar
Kerchman, V. I. & Frenkel, A. L. 1994 Interactions of coherent structures in a film flow – simulations of a highly nonlinear evolution equation. Theor. Comput. Fluid Dyn. 6, 235–254.Google Scholar
Kull, H. J. 1991 Theory of the Rayleigh–Taylor instability. Phys. Rep. 206 (5), 197–325.Google Scholar
Mensire, R., Wexler, J. S., Guibaud, A., Lorenceau, E. & Stone, H. A. 2016 Surfactant- and aqueous-foam-driven oil extraction from micropatterned surfaces. Langmuir 32 (49), 13149–13158.Google ScholarPubMed
Oron, A., Davis, S. H. & Bankoff, S. G. 1997 Long–scale evolution of thin liquid films. Rev. Mod. Phys. 69, 931–980.Google Scholar
Peng, J. & Zhu, K.-Q. 2010 Linear instability of two-fluid Taylor–Couette flow in the presence of surfactant. J. Fluid Mech. 651, 357–385.Google Scholar
Picardo, J. R., Radhakrishna, T. G. & Pushpavanam, S. 2016 Solutal Marangoni instability in layered two-phase flows. J. Fluid Mech. 793, 280–315.Google Scholar
Pozrikidis, C. 2004 Effect of inertia on the Marangoni instability of two-layer channel flow. Part I: numerical simulations. J. Engng Maths 50 (2–3), 311–327.Google Scholar
Rayleigh, Lord 1900 Investigation of the character of the equilibrium of an incompressible heavy fluid of variable density. In Scientific Papers, vol. II, pp. 200–207. Cambridge University Press.Google Scholar
Samanta, A. 2013 Effect of surfactant on two-layer channel flow. J. Fluid Mech. 735, 519–552.CrossRefGoogle Scholar
Samanta, A. 2014 Effect of surfactants on the instability of a two-layer film flow down an inclined plane. Phys. Fluids 26 (9), 094105.CrossRefGoogle Scholar
Schweiger, A. J.2013 Gravity, surfactants, and instabilities of two-layer shear flows. PhD thesis, University of Alabama.Google Scholar
Wei, H. H. 2005 On the flow-induced Marangoni instability due to the presence of surfactant. J. Fluid Mech. 544, 173–200.CrossRefGoogle Scholar
Wei, H. H. 2007 Role of base flows on surfactant-driven interfacial instabilities. Phys. Rev. E 75, 036306.Google Scholar
Yiantsios, S. G. & Higgins, B. G. 1988 Linear stability of plane Poiseuille flow of two superposed fluids. Phys. Fluids 31, 3225–3238.CrossRefGoogle Scholar
Yiantsios, S. G. & Higgins, B. G. 1989 Erratum: ‘Linear stability of plane Poiseuille flow of two superposed fluids’ [Phys. Fluids 31, 3225 (1988)]. Phys. Fluids A 1 (5), 897–897.Google Scholar
Yih, C. S. 1967 Instability due to viscosity stratification. J. Fluid Mech. 27, 337–352.Google Scholar