Published online by Cambridge University Press: 30 August 2016
Supercritical ship internal wave wakes with 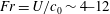 $Fr=U/c_{0}\sim 4{-}12$ (where
$Fr=U/c_{0}\sim 4{-}12$ (where 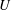 $U$ is the ship speed and
$U$ is the ship speed and 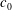 $c_{0}$ is the linear internal long-wave speed) are calculated by a strongly nonlinear two-layer model in three dimensions, accounting for the complex ship geometry, and compared with field measurements. The degree of nonlinearity, defined by the ship draught (
$c_{0}$ is the linear internal long-wave speed) are calculated by a strongly nonlinear two-layer model in three dimensions, accounting for the complex ship geometry, and compared with field measurements. The degree of nonlinearity, defined by the ship draught (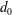 $d_{0}$) to average depth of pycnocline (
$d_{0}$) to average depth of pycnocline (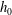 $h_{0}$) ratio, is explored in the range
$h_{0}$) ratio, is explored in the range 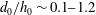 $d_{0}/h_{0}\sim 0.1{-}1.2$, comparing nonlinear and linear calculations. For
$d_{0}/h_{0}\sim 0.1{-}1.2$, comparing nonlinear and linear calculations. For 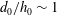 $d_{0}/h_{0}\sim 1$, the wave amplitude far downstream is overpredicted by up to 50 % by the linear method. The nonlinear trough amplitudes decay algebraically in the lateral coordinate with decay exponents in the range 0.16–0.61. The nonlinear leading trough is systematically somewhat ahead of the classical asymptotic pattern, and its amplitude and forerunning slope are appreciable, while the linear counterparts are very small. The calculated and asymptotic patterns are close for large
$d_{0}/h_{0}\sim 1$, the wave amplitude far downstream is overpredicted by up to 50 % by the linear method. The nonlinear trough amplitudes decay algebraically in the lateral coordinate with decay exponents in the range 0.16–0.61. The nonlinear leading trough is systematically somewhat ahead of the classical asymptotic pattern, and its amplitude and forerunning slope are appreciable, while the linear counterparts are very small. The calculated and asymptotic patterns are close for large 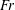 $Fr$. Field measurements in a Canadian fjord of the internal wave wake of a 221 m long cargo ship of dead weight 43 000 tonnes moving at
$Fr$. Field measurements in a Canadian fjord of the internal wave wake of a 221 m long cargo ship of dead weight 43 000 tonnes moving at 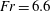 $Fr=6.6$ document a series of waves of 1–2 m isopycnal displacements at an off-track distance of 700 m. The nonlinear computations of a similar ship predict a wave train of height 1.5 m at a similar position, matching the field observation, whereas linear calculations give a wave train of height 2.3 m. Two- and three-layer theoretical models predict speeds that match the observed speeds of the second and third wave troughs. The observed leading signature of the diverging wave wake is moving at supercritical speed. This may be explained by the position and speed of the nonlinear wave slope moving ahead of the leading trough. Nonlinear computations of the surface velocity and strain rate compare well with measurements in the Loch Linnhe experiment of Watson et al. (J. Geophys. Res., vol. 97 (C6), 1992, pp. 9689–9703). The calculated nonlinear wave resistance of the observed cargo ship is comparable to the frictional force for
$Fr=6.6$ document a series of waves of 1–2 m isopycnal displacements at an off-track distance of 700 m. The nonlinear computations of a similar ship predict a wave train of height 1.5 m at a similar position, matching the field observation, whereas linear calculations give a wave train of height 2.3 m. Two- and three-layer theoretical models predict speeds that match the observed speeds of the second and third wave troughs. The observed leading signature of the diverging wave wake is moving at supercritical speed. This may be explained by the position and speed of the nonlinear wave slope moving ahead of the leading trough. Nonlinear computations of the surface velocity and strain rate compare well with measurements in the Loch Linnhe experiment of Watson et al. (J. Geophys. Res., vol. 97 (C6), 1992, pp. 9689–9703). The calculated nonlinear wave resistance of the observed cargo ship is comparable to the frictional force for 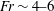 $Fr\sim 4{-}6$, exceeds the surface wave resistance and increases the total drag by 40 %. A linear force prediction is useless when
$Fr\sim 4{-}6$, exceeds the surface wave resistance and increases the total drag by 40 %. A linear force prediction is useless when 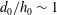 $d_{0}/h_{0}\sim 1$. The results show that nonlinearity of the dead water wake depends on the relative ship volume as well as the relative ship draught, with the pycnocline depth as the relevant length scale.
$d_{0}/h_{0}\sim 1$. The results show that nonlinearity of the dead water wake depends on the relative ship volume as well as the relative ship draught, with the pycnocline depth as the relevant length scale.