Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-22T15:12:02.039Z Has data issue: false hasContentIssue false
  • English
  • Français

The structure and dynamics of backflow in turbulent channels

Published online by Cambridge University Press:  07 October 2019

J. I. Cardesa Open the ORCID record for J. I. Cardesa [Opens in a new window] ,
J. P. Monty Open the ORCID record for J. P. Monty [Opens in a new window] ,
J. Soria Open the ORCID record for J. Soria [Opens in a new window]  and
M. S. Chong
J. I. Cardesa
Affiliation:
School of Aeronautics, Universidad Politécnica de Madrid, 28040 Madrid, Spain
J. P. Monty
Affiliation:
Department of Mechanical Engineering, University of Melbourne, Victoria 3010, Australia
J. Soria
Affiliation:
Laboratory for Turbulence Research in Aerospace and Combustion, Department of Mechanical and Aerospace Engineering, Monash University (Clayton Campus), Melbourne 3800, Australia
M. S. Chong
Affiliation:
Department of Mechanical Engineering, University of Melbourne, Victoria 3010, Australia
Get access Rights & Permissions [Opens in a new window]

Abstract

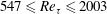A statistical description of flow regions with negative streamwise velocity is provided based on simulations of turbulent plane channels in the Reynolds number range $547\leqslant Re_{\unicode[STIX]{x1D70F}}\leqslant 2003$. It is found that regions of backflow are attached and their density per surface area – in wall units – is an increasing function of 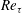$Re_{\unicode[STIX]{x1D70F}}$. Their size distribution along the three coordinates reveals that, even though in the mean they appear to be circular in the wall-parallel plane, they tend to become more elongated in the spanwise direction after reaching a certain height. Time-tracking of backflow regions in a 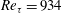$Re_{\unicode[STIX]{x1D70F}}=934$ simulation showed they convect downstream at the mean velocity corresponding to 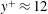$y^{+}\approx 12$, they seldom interact with other backflow events, their statistical signature extends in the streamwise direction for at least $300$ wall units, and they result from a complex interaction between regions of high and low spanwise vorticity far beyond the viscous sublayer. This could explain why some statistical aspects of these near-wall events do not scale in viscous units; they are dependent on the 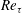$Re_{\unicode[STIX]{x1D70F}}$-dependent dynamics further away from the wall.

JFM classification

Turbulent Flows: Turbulence simulation Boundary Layers: Boundary layer structure Turbulent Flows: Turbulent boundary layers
Type
JFM Rapids
Information
Journal of Fluid Mechanics , Volume 880 , 10 December 2019 , R3
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

†

Present address: Institut de Mécanique des Fluides de Toulouse (IMFT), Université de Toulouse, 31400 Toulouse, France. Email address for correspondence: [email protected]

References

del Álamo, J. C. & Jiménez, J. 2003 Spectra of the very large anisotropic scales in turbulent channels. Phys. Fluids 15 (6), L41–L44.10.1063/1.1570830Google Scholar
del Álamo, J. C. & Jiménez, J. 2009 Estimation of turbulent convection velocities and corrections to Taylor’s approximation. J. Fluid Mech. 640, 5–26.10.1017/S0022112009991029Google Scholar
del Álamo, J. C., Jiménez, J., Zandonade, P. & Moser, R. D. 2004 Scaling of the energy spectra of turbulent channels. J. Fluid Mech. 500, 135–144.Google Scholar
Bauer, B. & Reynolds, M. 2008 Recovering data from scanned graphs: performance of Frantz’s g3data software. Behav. Res. Meth. 40 (3), 858–868.10.3758/BRM.40.3.858Google Scholar
Cardesa, J. I., Monty, J. P., Soria, J. & Chong, M. S. 2014 Skin-friction critical points in wall-bounded flows. In Journal of Physics: Conference Series, vol. 506, p. 012009. IOP Publishing.Google Scholar
Cardesa, J. I., Vela-Martín, A. & Jiménez, J. 2017 The turbulent cascade in five dimensions. Science 357 (6353), 782–784.Google Scholar
Diaz-Daniel, C., Laizet, S. & Vassilicos, J. C. 2017 Wall shear stress fluctuations: mixed scaling and their effects on velocity fluctuations in a turbulent boundary layer. Phys. Fluids 29 (5), 055102.10.1063/1.4984002Google Scholar
Eckelmann, H. 1974 The structure of the viscous sublayer and the adjacent wall region in a turbulent channel flow. J. Fluid Mech. 65 (3), 439–459.10.1017/S0022112074001479Google Scholar
El Khoury, G. K., Schlatter, P., Brethouwer, G. & Johansson, A. V. 2014 Turbulent pipe flow: statistics, re-dependence, structures and similarities with channel and boundary layer flows. J. Phys.: Conf. Ser. 506 (1), 012010.Google Scholar
Hoyas, S. & Jiménez, J. 2006 Scaling of the velocity fluctuations in turbulent channels up to Re = 2003. Phys. Fluids 18 (1), 011702.Google Scholar
Hu, Z. W., Morfey, C. L. & Sandham, N. D. 2006 Wall pressure and shear stress spectra from direct simulations of channel flow. AIAA J. 44 (7), 1541–1549.10.2514/1.17638Google Scholar
Jalalabadi, R. & Sung, H. J. 2018 Influence of backflow on skin friction in turbulent pipe flow. Phys. Fluids 30 (6), 065104.10.1063/1.5026998Google Scholar
Kim, J., Moin, P. & Moser, R. 1987 Turbulence statistics in fully developed channel flow at low Reynolds number. J. Fluid Mech. 177, 133166.Google Scholar
Lenaers, P., Li, Q., Brethouwer, G., Schlatter, P. & Örlü, R. 2012 Rare backflow and extreme wall-normal velocity fluctuations in near-wall turbulence. Phys. Fluids 24 (3), 035110.10.1063/1.3696304Google Scholar
Lozano-Durán, A. & Jiménez, J. 2014 Time-resolved evolution of coherent structures in turbulent channels: characterization of eddies and cascades. J. Fluid Mech. 759, 432–471.10.1017/jfm.2014.575Google Scholar
Spalart, P. R. & Coleman, G. N. 1997 Numerical study of a separation bubble with heat transfer. Eur. J. Mech. B/Fluids 16 (2), 169–189.Google Scholar
Willert, C. E., Cuvier, C., Foucaut, J. M., Klinner, J., Stanislas, M., Laval, J. P., Srinath, S., Soria, J., Amili, O., Atkinson, C. et al. 2018a Experimental evidence of near-wall reverse flow events in a zero pressure gradient turbulent boundary layer. Exp. Therm. Fluid Sci. 91, 320–328.Google Scholar
Willert, C., Soria, J., Cuvier, C., Foucaut, J. M. & Laval, J. P. 2018b Flow reversal in turbulent boundary layers with varying pressure gradients. In Proceedings of the 5th International Conference on Experimental Fluid Mechanics ICEFM 2018.Google Scholar
Willert, C., Soria, J., Cuvier, C., Foucaut, J. M. & Laval, J. P. 2018c Flow reversal in turbulent boundary layers with varying pressure gradients. In Proceedings of the 19th International Symposium on Applications of Laser and Imaging Techniques to Fluid Mechanics.Google Scholar