Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-23T14:12:37.991Z Has data issue: false hasContentIssue false
  • English
  • Français

Structure and dynamics of a laminar separation bubble near a wingtip

Published online by Cambridge University Press:  28 October 2021

Connor E. Toppings  and
Serhiy Yarusevych Open the ORCID record for Serhiy Yarusevych [Opens in a new window]
Connor E. Toppings
Affiliation:
Department of Mechanical and Mechatronics Engineering, University of Waterloo, Waterloo, ON N2L 3G1, Canada
Serhiy Yarusevych*
Affiliation:
Department of Mechanical and Mechatronics Engineering, University of Waterloo, Waterloo, ON N2L 3G1, Canada
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

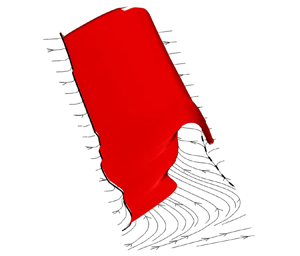
The three-dimensional flow topology of a laminar separation bubble forming on the suction surface of a semispan wing with an aspect ratio of $2.5$ and NACA 0018 airfoil section is characterised experimentally using surface pressure measurements and particle image velocimetry at a chord Reynolds number of $125\ 000$. In the inboard region of the wing, the separation bubble is essentially two-dimensional, and the transition process in the separated shear layer leads to periodic vortex shedding, which dominates the bubble dynamics, similar to two-dimensional separation bubbles. However, progressive spanwise changes in the mean structure and vortex dynamics occur near the wingtip, leading to an open separation and eventual suppression of the bubble. In the immediate proximity of the wingtip, the boundary layer remains attached, no vortex shedding occurs and the flow remains laminar, terminating separation bubble formation. Despite variations in the mean separation bubble topology and vortex dynamics along the span, the fundamental shedding characteristics remain nearly invariant across the portion of the wing where vortex shedding occurs, and the flow appears to lock onto a common instability mode across the span, leading to minimal changes in the mean bubble characteristics despite notable changes in the effective angle of attack along the span. A comparison with available surface flow visualisations from previous studies indicates that the observed changes to the mean bubble footprint along the span of the wing are similar across different geometries and flow characteristics, suggesting similarities in the three-dimensional bubble topology and dynamics on finite wings.

JFM classification

Boundary Layers: Boundary layer separation Vortex Flows: Vortex shedding Wakes/Jets: Separated flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 929 , 25 December 2021 , A39
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Alam, M. & Sandham, N.D. 2000 Direct numerical simulation of ‘short’ laminar separation bubbles with turbulent reattachment. J. Fluid Mech. 403, 223–250.CrossRefGoogle Scholar
Ananda, G.K., Selig, M.S. & Deters, R.W. 2018 Experiments of propeller-induced flow effects on a low-Reynolds-number wing. AIAA J. 56 (8), 3279–3294.CrossRefGoogle Scholar
Ananda, G.K., Sukumar, P.P. & Selig, M.S. 2015 Measured aerodynamic characteristics of wings at low Reynolds numbers. Aerosp. Sci. Technol. 42, 392–406.CrossRefGoogle Scholar
Awasthi, M., Moreau, D.J. & Doolan, C.J. 2018 Flow structure of a low aspect ratio wall-mounted airfoil operating in a low Reynolds number flow. Exp. Therm. Fluid Sci. 99, 94–116.CrossRefGoogle Scholar
Bastedo, W.G. & Mueller, T.J. 1986 Spanwise variation of laminar separation bubbles on wings at low Reynolds number. J. Aircraft 23 (9), 687–694.CrossRefGoogle Scholar
Ben Chiekh, M., Michard, M., Grosjean, N. & Béra, J.-C. 2004 Reconstruction temporelle d'un champ aérodynamique instationnaire à partir de mesures PIV non résolues dans le temps. In 9e Congrès Francophone de Vélocimétrie Laser, paper D.8.Google Scholar
Boutilier, M.S.H. & Yarusevych, S. 2012 a Parametric study of separation and transition characteristics over an airfoil at low Reynolds numbers. Exp. Fluids 52 (6), 1491–1506.CrossRefGoogle Scholar
Boutilier, M.S.H. & Yarusevych, S. 2012 b Separated shear layer transition over an airfoil at a low Reynolds number. Phys. Fluids 24 (8), 084105.CrossRefGoogle Scholar
Brendel, M. & Mueller, T.J. 1988 Boundary-layer measurements on an airfoil at low Reynolds numbers. J. Aircraft 25 (7), 612–617.CrossRefGoogle Scholar
Burgmann, S., Dannemann, J. & Schröder, W. 2008 Time-resolved and volumetric PIV measurements of a transitional separation bubble on an SD7003 airfoil. Exp. Fluids 44 (4), 609–622.CrossRefGoogle Scholar
Carmichael, B.H. 1981 Low Reynolds number airfoil survey. NASA Tech. Rep. CR-165803. Low Energy Transportation Systems.Google Scholar
Chen, P.-W., Bai, C.-J. & Wang, W.-C. 2016 Experimental and numerical studies of low aspect ratio wing at critical Reynolds number. Eur. J. Mech. (B/Fluids) 59, 161–168.CrossRefGoogle Scholar
Chen, Z.J., Qin, N. & Nowakowski, A.F. 2013 Three-dimensional laminar-separation bubble on a cambered thin wing at low Reynolds numbers. J. Aircraft 50 (1), 152–163.CrossRefGoogle Scholar
Délery, J.M. 2001 Robert legendre and Henri Werlé: toward the elucidation of three-dimensional separation. Annu. Rev. Fluid Mech. 33 (1), 129–154.CrossRefGoogle Scholar
Diwan, S.S. & Ramesh, O.N. 2009 On the origin of the inflectional instability of a laminar separation bubble. J. Fluid Mech. 629, 263–298.CrossRefGoogle Scholar
Dovgal, A.V., Kozlov, V.V. & Michalke, A. 1994 Laminar boundary layer separation: instability and associated phenomena. Prog. Aerosp. Sci. 30 (1), 61–94.CrossRefGoogle Scholar
Francis, T.B. & Katz, J. 1988 Observations on the development of a tip vortex on a rectangular hydrofoil. J. Fluids Engng 110 (2), 208–215.CrossRefGoogle Scholar
Garmann, D.J. & Visbal, M.R. 2017 Analysis of tip vortex near-wake evolution for stationary and oscillating wings. AIAA J. 55 (8), 2686–2702.CrossRefGoogle Scholar
Gaster, M. 1967 The structure and behaviour of laminar separation bubbles. Tech. Rep. Aeronautical Research Council Reports and Memoranda 3595.Google Scholar
Genç, M.S., Özkan, G., Özden, M., Kiriş, M.S. & Yildiz, R. 2018 Interaction of tip vortex and laminar separation bubble over wings with different aspect ratios under low Reynolds numbers. Proc. Inst. Mech. Engrs C: J. Mech. Engng Sci. 232 (22), 4019–4037.Google Scholar
Giuni, M. & Green, R.B. 2013 Vortex formation on squared and rounded tip. Aerosp. Sci. Technol. 29 (1), 191–199.CrossRefGoogle Scholar
Gresham, N.T., Wang, Z. & Gursul, I. 2010 Low Reynolds number aerodynamics of free-to-roll low aspect ratio wings. Exp. Fluids 49 (1), 11–25.CrossRefGoogle Scholar
Häggmark, C.P., Bakchinov, A.A. & Alfredsson, P.H. 2000 Experiments on a two–dimensional laminar separation bubble. Phil. Trans. R. Soc. Lond. A: Math. Phys. Engng Sci. 358 (1777), 3193–3205.CrossRefGoogle Scholar
Herbst, S.L., Hain, R. & Kähler, C.J. 2020 Low aspect ratio wing under large-scale turbulent inflow conditions at low Reynolds numbers. In Notes on Numerical Fluid Mechanics and Multidisciplinary Design, vol. 142, pp. 653–662. Springer Verlag.CrossRefGoogle Scholar
Hodson, H.P. & Howell, R.J. 2005 The role of transition in high-lift low-pressure turbines for aeroengines. Prog. Aerosp. Sci. 41 (6), 419–454.CrossRefGoogle Scholar
Horton, H.P. 1968 Laminar separation bubbles in two and three dimensional incompressible flow. Ph.D. thesis, University of London, London.Google Scholar
Hosseinverdi, S. & Fasel, H.F. 2019 Numerical investigation of laminar–turbulent transition in laminar separation bubbles: the effect of free-stream turbulence. J. Fluid Mech. 858, 714–759.CrossRefGoogle Scholar
Huang, R.F. & Lin, C.L. 1995 Vortex shedding and shear-layer instability of wing at low-Reynolds numbers. AIAA J. 33 (8), 1398–1403.CrossRefGoogle Scholar
Huber, A.F. & Mueller, T.J. 1987 The effect of trip wire roughness on the performance of the Wortmann FX 63-137 airfoil at low Reynolds numbers. Exp. Fluids 5 (4), 263–272.CrossRefGoogle Scholar
Hultquist, J.P.M. 1992 Constructing stream surfaces in steady 3D vector fields. In Proceedings Visualization ’92, pp. 171–178. IEEE Computer Society Press.Google Scholar
Istvan, M.S. & Yarusevych, S. 2018 Effects of free-stream turbulence intensity on transition in a laminar separation bubble formed over an airfoil. Exp. Fluids 59 (3), 52.CrossRefGoogle Scholar
Jeong, J. & Hussain, F. 1995 On the identification of a vortex. J. Fluid Mech. 285, 69–94.CrossRefGoogle Scholar
Kirk, T.M. & Yarusevych, S. 2017 Vortex shedding within laminar separation bubbles forming over an airfoil. Exp. Fluids 58 (5), 43.CrossRefGoogle Scholar
Kremheller, A. & Fasel, H. 2010 Water tunnel experiments on three dimensional separation bubbles on a flat plate. In 40th Fluid Dynamics Conference and Exhibit, paper 4738. AIAA.CrossRefGoogle Scholar
Kurelek, J.W. 2021 The vortex dynamics of laminar separation bubbles. PhD thesis, University of Waterloo.Google Scholar
Kurelek, J.W., Kotsonis, M. & Yarusevych, S. 2018 Transition in a separation bubble under tonal and broadband acoustic excitation. J. Fluid Mech. 853, 1–36.CrossRefGoogle Scholar
Kurelek, J.W., Lambert, A.R. & Yarusevych, S. 2016 Coherent structures in the transition process of a laminar separation bubble. AIAA J. 54 (8), 2295–2309.CrossRefGoogle Scholar
Kurelek, J.W., Yarusevych, S. & Kotsonis, M. 2019 Vortex merging in a laminar separation bubble under natural and forced conditions. Phys. Rev. Fluids 4 (6), 063903.CrossRefGoogle Scholar
Lamar, J.E. 1974 Extension of leading-edge-suction analogy to wings with separated flow around the side edges. NASA Tech. Rep. R-428.Google Scholar
Legrand, M., Nogueira, J. & Lecuona, A. 2011 a Flow temporal reconstruction from non-time-resolved data part I: mathematic fundamentals. Exp. Fluids 51 (4), 1047–1055.CrossRefGoogle Scholar
Legrand, M., Nogueira, J., Tachibana, S., Lecuona, A. & Nauri, S. 2011 b Flow temporal reconstruction from non time-resolved data part II: practical implementation, methodology validation, and applications. Exp. Fluids 51 (4), 861–870.CrossRefGoogle Scholar
Lengani, D., Simoni, D., Ubaldi, M. & Zunino, P. 2014 POD analysis of the unsteady behavior of a laminar separation bubble. Exp. Therm. Fluid Sci. 58, 70–79.CrossRefGoogle Scholar
Lengani, D., Simoni, D., Ubaldi, M., Zunino, P. & Bertini, F. 2017 a Analysis of the Reynolds stress component production in a laminar separation bubble. Intl J. Heat Fluid Flow 64, 112–119.CrossRefGoogle Scholar
Lengani, D., Simoni, D., Ubaldi, M., Zunino, P. & Bertini, F. 2017 b Experimental investigation on the time–space evolution of a laminar separation bubble by proper orthogonal decomposition and dynamic mode decomposition. Trans. ASME J. Turbomach. 139 (3), 031006.CrossRefGoogle Scholar
Lin, J.C.M. & Pauley, L.L. 1996 Low-Reynolds-number separation on an airfoil. AIAA J. 34 (8), 1570–1577.CrossRefGoogle Scholar
Lissaman, P.B.S. 1983 Low-Reynolds-number airfoils. Annu. Rev. Fluid Mech. 15 (1), 223–239.CrossRefGoogle Scholar
Liu, Y.-C. & Hsiao, F.-B. 2014 Experimental investigation on critical Reynolds numbers aerodynamic properties of low aspect ratios wings. Proc. Engng 79, 76–85.CrossRefGoogle Scholar
Lucca-Negro, O. & O'Doherty, T. 2001 Vortex breakdown: a review. Prog. Energy Combust. Sci. 27 (4), 431–481.CrossRefGoogle Scholar
Marchman, J.F. & Abtahi, A. 1985 Aerodynamics of an aspect ratio 8 wing at low Reynolds numbers. J. Aircraft 22 (7), 628–634.CrossRefGoogle Scholar
Marxen, O., Kotapati, R.B., Mittal, R. & Zaki, T. 2015 Stability analysis of separated flows subject to control by zero-net-mass-flux jet. Phys. Fluids 27 (2), 024107.CrossRefGoogle Scholar
Marxen, O., Lang, M. & Rist, U. 2013 Vortex formation and vortex breakup in a laminar separation bubble. J. Fluid Mech. 728, 58–90.CrossRefGoogle Scholar
Michalke, A. 1991 On the instability of wall-boundary layers close to separation. In Separated Flows and Jets (ed. V. Kozlov & A.V. Dovgal), pp. 557–564. Springer Berlin Heidelberg.CrossRefGoogle Scholar
Michelis, T., Yarusevych, S. & Kotsonis, M. 2018 On the origin of spanwise vortex deformations in laminar separation bubbles. J. Fluid Mech. 841, 81–108.CrossRefGoogle Scholar
Mizoguchi, M. & Itoh, H. 2013 Effect of aspect ratio on aerodynamic characteristics at low Reynolds numbers. AIAA J. 51 (7), 1631–1639.CrossRefGoogle Scholar
Moffat, R.J. 1988 Describing the uncertainties in experimental results. Exp. Therm. Fluid Sci. 1 (1), 3–17.CrossRefGoogle Scholar
Mueller, T.J. & DeLaurier, J.D. 2003 Aerodynamics of small vehicles. Annu. Rev. Fluid Mech. 35 (1), 89–111.CrossRefGoogle Scholar
Nati, A., de Kat, R., Scarano, F. & van Oudheusden, B.W. 2015 Dynamic pitching effect on a laminar separation bubble. Exp. Fluids 56 (9), 172.CrossRefGoogle Scholar
O'Meara, M.M. & Mueller, T.J. 1987 Laminar separation bubble characteristics on an airfoil at low Reynolds numbers. AIAA J. 25 (8), 1033–1041.CrossRefGoogle Scholar
van Oudheusden, B.W., Scarano, F., van Hinsberg, N.P. & Watt, D.W. 2005 Phase-resolved characterization of vortex shedding in the near wake of a square-section cylinder at incidence. Exp. Fluids 39 (1), 86–98.CrossRefGoogle Scholar
Perry, A.E., Hornung, H., Perry, A.E. & Hornung, H. 1984 Some aspects of three-dimensional separation. II - vortex skeletons. Z. Flugwiss. Weltraumforsch. 8, 155–160.Google Scholar
Prandtl, L. 1904 Über Flüssigkeitsbewegung bei sehr kleiner Reibung. In Verhandlungen des III. Internationalen Mathematiker-Kongresses, pp. 484–491. Heidelberg.Google Scholar
Pröbsting, S. & Yarusevych, S. 2015 Laminar separation bubble development on an airfoil emitting tonal noise. J. Fluid Mech. 780, 167–191.CrossRefGoogle Scholar
Rist, U., Lang, M. & Wagner, S. 2004 Investigations on controlled transition development in a laminar separation bubble by means of LDA and PIV. Exp. Fluids 36 (1), 43–52.CrossRefGoogle Scholar
Rist, U., Maucher, U. & Wagner, S. 1996 Direct numerical simulation of some fundamental problems related to transition in laminar separation bubbles. In Computational Fluid Dynamics ’96, pp. 319–325. Wiley.Google Scholar
Rodríguez, D., Gennaro, E.M. & Juniper, M.P. 2013 The two classes of primary modal instability in laminar separation bubbles. J. Fluid Mech. 734, 1–11.CrossRefGoogle Scholar
Rodríguez, D. & Theofilis, V. 2010 Structural changes of laminar separation bubbles induced by global linear instability. J. Fluid Mech. 655, 280–305.CrossRefGoogle Scholar
Scarano, F. & Riethmuller, M.L. 2000 Advances in iterative multigrid PIV image processing. Exp. Fluids 29 (7), S051–S060.CrossRefGoogle Scholar
Shields, M. & Mohseni, K. 2012 Effects of sideslip on the aerodynamics of low-aspect-ratio low-Reynolds-number wings. AIAA J. 50 (1), 85–99.CrossRefGoogle Scholar
Simoni, D., Lengani, D., Ubaldi, M., Zunino, P. & Dellacasagrande, M. 2017 Inspection of the dynamic properties of laminar separation bubbles: free-stream turbulence intensity effects for different Reynolds numbers. Exp. Fluids 58 (6), 66.CrossRefGoogle Scholar
Sirovich, L. 1987 Turbulence and the dynamics of coherent structures. I. Coherent structures. Q. Appl. Math. 45 (3), 561–571.CrossRefGoogle Scholar
Smith, T.A. & Ventikos, Y. 2021 Wing-tip vortex dynamics at moderate Reynolds numbers. Phys. Fluids 33 (3), 035111.CrossRefGoogle Scholar
Surana, A., Grunberg, O. & Haller, G. 2006 Exact theory of three-dimensional flow separation. Part 1. Steady separation. J. Fluid Mech. 564, 57–103.CrossRefGoogle Scholar
Tani, I. 1964 Low-speed flows involving bubble separations. Prog. Aerosp. Sci. 5, 70–103.CrossRefGoogle Scholar
Tobak, M. & Peake, D.J. 1982 Topology of three-dimensional separated flows. Annu. Rev. Fluid Mech. 14 (1), 61–85.CrossRefGoogle Scholar
Toppings, C.E., Kurelek, J.W. & Yarusevych, S. 2021 Laminar separation bubble development on a finite wing. AIAA J. 59 (8), 2855–2867.Google Scholar
Torres, G.E. & Mueller, T.J. 2004 Low aspect ratio aerodynamics at low Reynolds numbers. AIAA J. 42 (5), 865–873.CrossRefGoogle Scholar
Wang, K.C. 1970 Three-dimensional boundary layer near the plane of symmetry of a spheroid at incidence. J. Fluid Mech. 43 (1), 187–209.CrossRefGoogle Scholar
Watmuff, J.H. 1999 Evolution of a wave packet into vortex loops in a laminar separation bubble. J. Fluid Mech. 397, 119–169.CrossRefGoogle Scholar
Westerweel, J. & Scarano, F. 2005 Universal outlier detection for PIV data. Exp. Fluids 39 (6), 1096–1100.CrossRefGoogle Scholar
Wieneke, B. 2005 Stereo-PIV using self-calibration on particle images. Exp. Fluids 39 (2), 267–280.CrossRefGoogle Scholar
Wieneke, B. 2015 PIV uncertainty quantification from correlation statistics. Meas. Sci. Technol. 26 (7), 074002.CrossRefGoogle Scholar
Wu, J.Z., Tramel, R.W., Zhu, F.L. & Yin, X.Y. 2000 A vorticity dynamics theory of three-dimensional flow separation. Phys. Fluids 12 (8), 1932–1954.CrossRefGoogle Scholar
Yarusevych, S., Sullivan, P.E. & Kawall, J.G. 2009 On vortex shedding from an airfoil in low-Reynolds-number flows. J. Fluid Mech. 632, 245–271.CrossRefGoogle Scholar
Yates, L.A. & Chapman, G.T. 1988 Numerical investigation of crossflow separation on a three-caliber tangent ogive cylinder. AIAA J. 26 (10), 1223–1230.CrossRefGoogle Scholar
Yen, S.C. & Huang, L.C. 2009 Flow patterns and aerodynamic performance of unswept and swept-back wings. J. Fluids Engng 131 (11), 111101.CrossRefGoogle Scholar

Toppings and Yarusevych supplementary movie 1

Side-view phase averaged contours of spanwise vorticity and spanwise velocity, showing vortex shedding cycle at z/c=1.25.

Download Toppings and Yarusevych supplementary movie 1(Video)
Video 1 MB

Toppings and Yarusevych supplementary movie 2

Side-view phase averaged contours of spanwise vorticity and spanwise velocity, showing vortex shedding cycle at at z/c=2.00.

Download Toppings and Yarusevych supplementary movie 2(Video)
Video 1.2 MB

Toppings and Yarusevych supplementary movie 3

Side-view phase averaged contours of spanwise vorticity and spanwise velocity, showing vortex shedding cycle at at z/c=2.15.

Download Toppings and Yarusevych supplementary movie 3(Video)
Video 770.2 KB

Toppings and Yarusevych supplementary movie 4

Side-view phase averaged contours of spanwise vorticity and spanwise velocity, showing vortex shedding cycle at at z/c=2.25.

Download Toppings and Yarusevych supplementary movie 4(Video)
Video 552.6 KB

Toppings and Yarusevych supplementary movie 5

Top-view phase averaged contours of streamwise velocity, showing vortex shedding cycle.

Download Toppings and Yarusevych supplementary movie 5(Video)
Video 930.3 KB