Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-17T05:18:41.622Z Has data issue: false hasContentIssue false
  • English
  • Français

Streamwise inclination angle of large wall-attached structures in turbulent boundary layers

Published online by Cambridge University Press:  02 September 2019

Rahul Deshpande Open the ORCID record for Rahul Deshpande [Opens in a new window] ,
Jason P. Monty Open the ORCID record for Jason P. Monty [Opens in a new window]  and
Ivan Marusic Open the ORCID record for Ivan Marusic [Opens in a new window]
Rahul Deshpande*
Affiliation:
Department of Mechanical Engineering, University of Melbourne, Parkville, VIC 3010, Australia
Jason P. Monty
Affiliation:
Department of Mechanical Engineering, University of Melbourne, Parkville, VIC 3010, Australia
Ivan Marusic
Affiliation:
Department of Mechanical Engineering, University of Melbourne, Parkville, VIC 3010, Australia
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

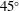The streamwise inclination angle of large wall-attached structures, in the log region of a canonical turbulent boundary layer, is estimated via spectral coherence analysis, and is found to be approximately $45^{\circ }$. This is consistent with assumptions used in prior attached eddy model-based simulations. Given that the inclination angle obtained via standard two-point correlations is influenced by the range of scales in the turbulent flow (Marusic, Phys. Fluids, vol. 13 (3), 2001, pp. 735–743), the present result is obtained by isolating the large wall-attached structures from the rest of the turbulence. This is achieved by introducing a spanwise offset between two hot-wire probes, synchronously measuring the streamwise velocity at a near-wall and log-region reference location, to assess the wall coherence. The methodology is shown to be effective by applying it to data sets across Reynolds numbers, $Re_{\unicode[STIX]{x1D70F}}\sim O(10^{3})$–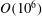$O(10^{6})$.

JFM classification

Boundary Layers: Boundary layer structure Turbulent Flows: Turbulent boundary layers Turbulent Flows: Turbulence modelling
Type
JFM Rapids
Information
Journal of Fluid Mechanics , Volume 877 , 25 October 2019 , R4
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adrian, R. J., Meinhart, C. D. & Tomkins, C. D. 2000 Vortex organization in the outer region of the turbulent boundary layer. J. Fluid Mech. 422, 1–54.10.1017/S0022112000001580Google Scholar
Alving, A. E., Smits, A. J. & Watmuff, J. H. 1990 Turbulent boundary layer relaxation from convex curvature. J. Fluid Mech. 211, 529–556.10.1017/S0022112090001689Google Scholar
Baars, W. J., Hutchins, N. & Marusic, I. 2016 Spectral stochastic estimation of high-Reynolds-number wall-bounded turbulence for a refined inner–outer interaction model. Phys. Rev. Fluids 1 (5), 054406.10.1103/PhysRevFluids.1.054406Google Scholar
Baars, W. J., Hutchins, N. & Marusic, I. 2017 Self-similarity of wall-attached turbulence in boundary layers. J. Fluid Mech. 823, R2.10.1017/jfm.2017.357Google Scholar
Baidya, R., Baars, W. J., Zimmerman, S., Samie, M., Hearst, R. J., Dogan, E., Mascotelli, L., Zheng, X., Bellani, G., Talamelli, A. et al. 2019 Simultaneous skin friction and velocity measurements in high Reynolds number pipe and boundary layer flows. J. Fluid Mech. 871, 377–400.10.1017/jfm.2019.303Google Scholar
Baidya, R., Philip, J., Hutchins, N., Monty, J. P. & Marusic, I. 2017 Distance-from-the-wall scaling of turbulent motions in wall-bounded flows. Phys. Fluids 29 (2), 020712.10.1063/1.4974354Google Scholar
Baidya, R., Philip, J., Monty, J. P., Hutchins, N. & Marusic, I. 2014 Comparisons of turbulence stresses from experiments against the attached eddy hypothesis in boundary layers. In Proceedings of 19th Australasan Fluid Mechanics Conference, Melbourne, Australia.Google Scholar
Brown, G. L. & Thomas, A. S. W. 1977 Large structure in a turbulent boundary layer. Phys. Fluids 20 (10), S243–S252.10.1063/1.861737Google Scholar
Carper, M. A. & Porte-Agel, F. 2004 The role of coherent structures in subfilter-scale dissipation of turbulence measured in the atmospheric surface layer. J. Turbul. 5, 32–55.Google Scholar
Chandran, D., Baidya, R., Monty, J. P. & Marusic, I. 2017 Two-dimensional energy spectra in high-Reynolds-number turbulent boundary layers. J. Fluid Mech. 826, R1.10.1017/jfm.2017.359Google Scholar
Head, M. R. & Bandyopadhyay, P. 1981 New aspects of turbulent boundary-layer structure. J. Fluid Mech. 107, 297–338.10.1017/S0022112081001791Google Scholar
Hutchins, N., Chauhan, K., Marusic, I., Monty, J. & Klewicki, J. 2012 Towards reconciling the large-scale structure of turbulent boundary layers in the atmosphere and laboratory. Boundary-Layer Meteorol. 145 (2), 273–306.10.1007/s10546-012-9735-4Google Scholar
Hutchins, N. & Marusic, I. 2007 Evidence of very long meandering features in the logarithmic region of turbulent boundary layers. J. Fluid Mech. 579, 1–28.10.1017/S0022112006003946Google Scholar
Jones, M. B., Marusic, I. & Perry, A. E. 2001 Evolution and structure of sink-flow turbulent boundary layers. J. Fluid Mech. 428, 1–27.10.1017/S0022112000002597Google Scholar
Marusic, I. 2001 On the role of large-scale structures in wall turbulence. Phys. Fluids 13 (3), 735–743.10.1063/1.1343480Google Scholar
Marusic, I. & Heuer, W. D. C. 2007 Reynolds number invariance of the structure inclination angle in wall turbulence. Phys. Rev. Lett. 99 (11), 114504.10.1103/PhysRevLett.99.114504Google Scholar
Marusic, I., Kunkel, G. J. & Porte-Agel, F. 2001 Experimental study of wall boundary conditions for large-eddy simulation. J. Fluid Mech. 446, 309–320.10.1017/S0022112001005924Google Scholar
Marusic, I. & Monty, J. P. 2019 Attached eddy model of wall turbulence. Annu. Rev. Fluid Mech. 51, 49–74.10.1146/annurev-fluid-010518-040427Google Scholar
Moin, P. & Kim, J. 1985 The structure of the vorticity field in turbulent channel flow. Part 1. Analysis of instantaneous fields and statistical correlations. J. Fluid Mech. 155, 441–464.10.1017/S0022112085001896Google Scholar
Perry, A. E. & Marusic, I. 1995 A wall-wake model for the turbulence structure of boundary layers. Part 1. Extension of the attached eddy hypothesis. J. Fluid Mech. 298, 361–388.10.1017/S0022112095003351Google Scholar
Perry, A. E., Uddin, A. K. M. & Marusic, I. 1992 An experimental and computational study on the orientation of attached eddies in turbulent boundary layers. In Proceedings of the 11th Australasian Fluid Mechanics Conference, Hobart, Australia.Google Scholar
Piomelli, U. & Balaras, E. 2002 Wall-layer models for large-eddy simulations. Annu. Rev. Fluid Mech. 34 (1), 349–374.10.1146/annurev.fluid.34.082901.144919Google Scholar
Piomelli, U., Ferziger, J., Moin, P. & Kim, J. 1989 New approximate boundary conditions for large eddy simulations of wall-bounded flows. Phys. Fluids A 1 (6), 1061–1068.10.1063/1.857397Google Scholar
Robinson, S. K. 1991 Coherent motions in the turbulent boundary layer. Annu. Rev. Fluid Mech. 23 (1), 601–639.10.1146/annurev.fl.23.010191.003125Google Scholar
Sillero, J. A., Jiménez, J. & Moser, R. D. 2013 One-point statistics for turbulent wall-bounded flows at Reynolds numbers up to 𝛿+ ≈ 2000. Phys. Fluids 25 (10), 105102.10.1063/1.4823831Google Scholar
de Silva, C. M., Squire, D. T., Hutchins, N. & Marusic, I. 2015 Towards capturing large scale coherent structures in boundary layers using particle image velocimetry. In Proceedings of the 7th Australian Conference on Laser Diagnostics in Fluid Mechanics and Combustion, Melbourne, Australia.Google Scholar
Uddin, A. K. M.1994 The structure of a turbulent boundary layer. PhD thesis, University of Melbourne.Google Scholar