Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-27T09:30:34.598Z Has data issue: false hasContentIssue false
  • English
  • Français

Streaming-potential phenomena in the thin-Debye-layer limit. Part 1. General theory

Published online by Cambridge University Press:  19 September 2011

Ehud Yariv ,
Ory Schnitzer  and
Itzchak Frankel
Ehud Yariv*
Affiliation:
Department of Mathematics, Technion – Israel Institute of Technology, Haifa 32000, Israel
Ory Schnitzer
Affiliation:
Department of Mathematics, Technion – Israel Institute of Technology, Haifa 32000, Israel
Itzchak Frankel
Affiliation:
Department of Aerospace Engineering, Technion – Israel Institute of Technology, Haifa 32000, Israel
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Electrokinetic streaming-potential phenomena are driven by imposed relative motion between liquid electrolytes and charged solids. Owing to non-uniform convective ‘surface’ current within the Debye layer Ohmic currents from the electro-neutral bulk are required to ensure charge conservation thereby inducing a bulk electric field. This, in turn, results in electro-viscous drag enhancement. The appropriate modelling of these phenomena in the limit of thin Debye layers 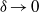( denoting the dimensionless Debye thickness) has been a matter of ongoing controversy apparently settled by Cox’s seminal analysis (J. Fluid Mech., vol. 338, 1997, p. 1). This analysis predicts electro-viscous forces that scale as 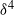resulting from the perturbation of the original Stokes flow with the Maxwell-stress contribution only appearing at higher orders. Using scaling analysis we clarify the distinction between the normalizations pertinent to field- and motion-driven electrokinetic phenomena, respectively. In the latter class we demonstrate that the product of the Hartmann & Péclet numbers is 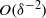contrary to Cox (1997) where both parameters are assumed 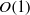. We focus on the case where motion-induced fields are comparable to the thermal scale and accordingly present a singular-perturbation analysis for the limit where the Hartmann number is 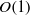and the Péclet number is 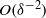. Electric-current matching between the Debye layer and the electro-neutral bulk provides an inhomogeneous Neumann condition governing the electric field in the latter. This field, in turn, results in a velocity perturbation generated by a Smoluchowski-type slip condition. Owing to the dominant convection, the present analysis yields an asymptotic structure considerably simpler than that of Cox (1997): the electro-viscous effect now already appears at and is contributed by both Maxwell and viscous stresses. The present paradigm is illustrated for the prototypic problem of a sphere sedimenting in an unbounded fluid domain with the resulting drag correction differing from that calculated by Cox (1997). Independently of current matching, salt-flux matching between the Debye layer and the bulk domain needs also to be satisfied. This subtle point has apparently gone unnoticed in the literature, perhaps because it is trivially satisfied in field-driven problems. In the present limit this requirement seems incompatible with the uniform salt distribution in the convection-dominated bulk domain. This paradox is resolved by identifying the dual singularity associated with the limit 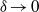in motion-driven problems resulting in a diffusive layer of 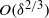thickness beyond the familiar 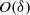-wide Debye layer.

JFM classification

Complex Fluids: Colloids Low-Reynolds-number flows: Low-Reynolds-number flows Micro-/Nano-fluid dynamics: Micro-/Nano-fluid dynamics
Type
Papers
Information
Journal of Fluid Mechanics , Volume 685 , 25 October 2011 , pp. 306 - 334
Copyright
Copyright © Cambridge University Press 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Alexander, B. M. & Prieve, D. C. 1987 A hydrodynamic technique for measurement of colloidal forces. Langmuir 3 (5), 788–795.CrossRefGoogle Scholar
2. Anderson, J. L. 1989 Colloid transport by interfacial forces. Annu. Rev. Fluid Mech. 30, 139–165.CrossRefGoogle Scholar
3. Bike, S. G., Lazarro, L. & Prieve, D. C. 1995 Electrokinetic lift of a sphere moving in slow shear flow parallel to a wall I. Experiment. J. Colloid Interface Sci. 175 (2), 411–421.CrossRefGoogle Scholar
4. Bike, S. G. & Prieve, D. C. 1990 Electrohydrodynamic lubrication with thin double layers. J. Colloid Interface Sci. 136 (1), 95–112.CrossRefGoogle Scholar
5. Bike, S. G. & Prieve, D. C. 1992 Electrohydrodynamics of thin double layers: a model for the streaming potential profile. J. Colloid Interface Sci. 154, 87–96.CrossRefGoogle Scholar
6. Bike, S. G. & Prieve, D. C. 1995 Electrokinetic lift of a sphere moving in slow shear flow parallel to a wall II. Theory. J. Colloid Interface Sci. 175 (2), 422–434.CrossRefGoogle Scholar
7. Boléve, A., Crespy, A., Revil, A., Janod, F. & Mattiuzzo, J. L. 2007 Streaming potentials of granular media: influence of the Dukhin and Reynolds numbers. J. Geophys. Res. 112, B08204.CrossRefGoogle Scholar
8. Booth, F. 1950 The electroviscous effect for suspensions of solid spherical particles. Proc. R. Soc. Lond. A 203 (1075), 533–551.Google Scholar
9. Booth, F. 1954 Sedimentation potential and velocity of solid spherical particles. J. Chem. Phys. 22, 1956–1968.CrossRefGoogle Scholar
10. Brenner, H. 1964 The Stokes resistance of an arbitrary particle – IV. Arbitrary fields of flow. Chem. Engng Sci. 19, 703–727.CrossRefGoogle Scholar
11. Cox, R. G. 1997 Electroviscous forces on a charged particle suspended in a flowing liquid. J. Fluid Mech. 338, 1–34.CrossRefGoogle Scholar
12. Doi, M. & Makino, M. 2008 Electrokinetic boundary condition compatible with the Onsager reciprocal relation in the thin double layer approximation. J. Chem. Phys. 128, 044715.CrossRefGoogle ScholarPubMed
13. Happel, J. & Brenner, H. 1965 Low Reynolds Number Hydrodynamics. Prentice-Hall.Google Scholar
14. Hinch, E. J. & Sherwood, J. D. 1983 Primary electroviscous effect in a suspension of spheres with thin double layers. J. Fluid Mech. 132, 337–347.CrossRefGoogle Scholar
15. Lac, E. & Sherwood, J. D. 2009 Streaming potential generated by a drop moving along the centreline of a capillary. J. Fluid Mech. 640, 55–77.CrossRefGoogle Scholar
16. Leal, L. G. 2007 Advanced Transport Phenomena: Fluid Mechanics and Convective Transport Processes. Cambridge University Press.CrossRefGoogle Scholar
17. Lyklema, J. 1995 Fundamentals of Interface and Colloid Science, vol. II. Academic.Google Scholar
18. Ohshima, H., Healy, T. W., White, L. R. & O’Brien, R. W. 1984 Sedimentation velocity and potential in a dilute suspension of charged spherical colloidal particles. J. Chem. Soc. Faraday Trans. 80 (10), 1299–1317.CrossRefGoogle Scholar
19. Prieve, D. C., Ebel, J. P., Anderson, J. L. & Lowell, M. E. 1984 Motion of a particle generated by chemical gradients. Part 2. Electrolytes. J. Fluid Mech. 148, 247–269.CrossRefGoogle Scholar
20. Rubinstein, I. & Zaltzman, B. 2001 Electro-osmotic slip of the second kind and instability in concentration polarization at electrodialysis membranes. Math. Models Meth. Appl. Sci. 11, 263–300.CrossRefGoogle Scholar
21. Russel, W. B. 1978 The rheology of suspensions of charged rigid spheres. J. Fluid Mech. 85 (2), 209–232.CrossRefGoogle Scholar
22. Saville, D. A. 1977 Electrokinetic effects with small particles. Annu. Rev. Fluid Mech. 9, 321–337.CrossRefGoogle Scholar
23. Sherwood, J. D. 1980 The primary electroviscous effect in a suspension of spheres. J. Fluid Mech. 101 (3), 609–629.CrossRefGoogle Scholar
24. Sherwood, J. D. 2007 Streaming potential generated by two-phase flow in a capillary. Phys. Fluids 19, 053101.CrossRefGoogle Scholar
25. Sherwood, J. D. 2008 Streaming potential generated by a long viscous drop in a capillary. Langmuir 24 (18), 10011–10018.CrossRefGoogle Scholar
26. Sherwood, J. D. 2009 Streaming potential generated by a small charged drop in Poiseuille flow. Phys. Fluids 21, 013101.CrossRefGoogle Scholar
27. Smoluchowski, M. 1921 Elektrische Endosmose und Strömungsströme. In Handbuch der Elektrizität und des Magnetismus, Band II, Stationaire Ströme (ed. Graetz, L. ). Barth.Google Scholar
28. Tabatabaei, S. M. & van de Ven, T. G. M. 2010 Tangential electroviscous drag on a sphere surrounded by a thin double layer near a wall for arbitrary particle–wall separations. J. Fluid Mech. 656, 360–406.CrossRefGoogle Scholar
29. Tabatabaei, S. M., van de Ven, T. G. M. & Rey, A. D. 2006 Electroviscous sphere–wall interactions. J. Colloid Interface Sci. 301 (1), 291–301.CrossRefGoogle ScholarPubMed
30. Van Dyke, M. 1964 Perturbation Methods in Fluid Mechanics. Academic.Google Scholar
31. van de Ven, T. G. M., Warszynski, P. & Dukhin, S. S. 1993a Attractive electroviscous forces. Colloids Surf. A 79 (1), 33–41.CrossRefGoogle Scholar
32. van de Ven, T. G. M., Warszynski, P. & Dukhin, S. S. 1993b Electrokinetic lift of small particles. J. Colloid Interface Sci. 157 (2), 328–331.CrossRefGoogle Scholar
33. Warszynski, P. & van de Ven, T. G. M. 2000 Electroviscous forces on a charged cylinder moving near a charged wall. J. Colloid Interface Sci. 223, 1–15.CrossRefGoogle Scholar
34. Yariv, E. 2010 An asymptotic derivation of the thin-Debye-layer limit for electrokinetic phenomena. Chem. Engng Commun. 197, 3–17.CrossRefGoogle Scholar