Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-17T13:17:45.331Z Has data issue: false hasContentIssue false
  • English
  • Français

Strato-rotational instability without resonance

Published online by Cambridge University Press:  10 May 2018

Chen Wang Open the ORCID record for Chen Wang [Opens in a new window]  and
Neil J. Balmforth Open the ORCID record for Neil J. Balmforth [Opens in a new window]
Chen Wang*
Affiliation:
Department of Mathematics, University of British Columbia, Vancouver, BC V6T 1Z2, Canada
Neil J. Balmforth
Affiliation:
Department of Mathematics, University of British Columbia, Vancouver, BC V6T 1Z2, Canada
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Strato-rotational instability (SRI) is normally interpreted as the resonant interactions between normal modes of the internal or Kelvin variety in three-dimensional settings in which the stratification and rotation are orthogonal to both the background flow and its shear. Using a combination of asymptotic analysis and numerical solution of the linear eigenvalue problem for plane Couette flow, it is shown that such resonant interactions can be destroyed by certain singular critical levels. These levels are not classical critical levels, where the phase speed $c$ of a normal mode matches the mean flow speed 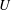$U$ , but are a different type of singularity where 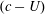$(c-U)$ matches a characteristic gravity-wave speed 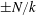$\pm N/k$ , based on the buoyancy frequency 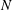$N$ and streamwise horizontal wavenumber 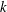$k$ . Instead, it is shown that a variant of SRI can occur due to the coupling of a Kelvin or internal wave to such ‘baroclinic’ critical levels. Two characteristic situations are identified and explored, and the conservation law for pseudo-momentum is used to rationalize the physical mechanism of instability. The critical level coupling removes the requirement for resonance near specific wavenumbers 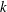$k$ , resulting in an extensive continuous band of unstable modes.

JFM classification

Instability: Instability Geophysical and Geological Flows: Internal waves Geophysical and Geological Flows: Stratified flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 846 , 10 July 2018 , pp. 815 - 833
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Badulin, S. I., Shrira, V. I. & Tsimring, L. Sh. 1985 The trapping and vertical focusing of internal waves in a pycnocline due to the horizontal inhomogeneities of density and currents. J. Fluid Mech. 158, 199–218.CrossRefGoogle Scholar
Balmforth, N. J. 1999 Shear instability in shallow water. J. Fluid Mech. 387, 97–127.CrossRefGoogle Scholar
Basovich, A. Y. & Tsimring, L. Sh. 1984 Internal waves in a horizontally inhomogeneous flow. J. Fluid Mech. 142, 233–249.CrossRefGoogle Scholar
Billant, P. & Le Dizès, S. 2009 Waves on a columnar vortex in a strongly stratified fluid. Phys. Fluids 21, 106602.CrossRefGoogle Scholar
Bühler, O. 2014 Waves and Mean Flows. Cambridge University Press.CrossRefGoogle Scholar
Dubrulle, B., Marié, L., Normand, Ch., Richard, D., Hersant, F. & Zahn, J.-P. 2005 A hydrodynamic shear instability in stratified disks. Astron. Astrophys. 429, 1–13.CrossRefGoogle Scholar
Howard, L. N. 1961 Note on a paper of John W. Miles. J. Fluid Mech. 10, 509–512.CrossRefGoogle Scholar
Ibanez, R., Swinney, H. L. & Rodenborn, B. 2016 Observations of the stratorotational instability in rotating concentric cylinders. Phys. Rev. Fluids 1, 053601.CrossRefGoogle Scholar
Kubokawa, A. 1984 Instability of a geostrophic front and its energetics. Geophys. Astrophys. Fluid Dyn. 33, 223–257.CrossRefGoogle Scholar
Le Bars, M. & Le Gal, P. 2007 Experimental analysis of the stratorotational instability in a cylindrical Couette flow. Phys. Rev. Lett. 99, 064502.CrossRefGoogle Scholar
Leclercq, C., Nguyen, F. & Kerswell, R. R. 2016 Connections between centrifugal, stratorotational, and radiative instabilitiesin viscous Taylor–Couette flow. Phys. Rev. E 94, 043103.Google Scholar
Le Dizès, S. & Billant, P. 2009 Radiative instability in stratified vortices. Phys. Fluids 21, 096602.CrossRefGoogle Scholar
Le Dizès, S. & Riedinger, X. 2010 The strato-rotational instability of Taylor–Couette and Keplerian flows. J. Fluid Mech. 660, 147–161.CrossRefGoogle Scholar
Miles, J. W. 1961 On the stability of heterogeneous shear flows. J. Fluid Mech. 10, 496–508.CrossRefGoogle Scholar
Molemaker, M. J., McWilliams, J. C. & Yavneh, I. 2001 Instability and equilibration of centrifugally stable stratified Taylor–Couette flow. Phys. Rev. Lett. 86, 5270–5273.CrossRefGoogle ScholarPubMed
Olbers, D. J. 1981 The propagation of internal waves in a geostrophic current. J. Phys. Oceanogr. 11, 1224–1233.2.0.CO;2>CrossRefGoogle Scholar
Park, J. & Billant, P. 2013 The stably stratified Taylor–Couette flow is always unstable except for solid-body rotation. J. Fluid Mech. 725, 262–280.CrossRefGoogle Scholar
Shalybkov, D. & Rüdiger, G. 2005 Stability of density-stratified viscous Taylor–Couette flows. Astron. Astrophys. 438, 411–417.CrossRefGoogle Scholar
Staquet, C. & Huerre, G. 2002 On transport across a barotropic shear flow by breaking inertia-gravity waves. Phys. Fluids 14, 1993–2006.CrossRefGoogle Scholar
Vanneste, J. & Yavneh, I. 2007 Unbalanced instabilities of rapidly rotating stratified shear flows. J. Fluid Mech. 584, 373–396.CrossRefGoogle Scholar
Yavneh, I., McWilliams, J. C. & Molemaker, M. J. 2001 Non-axisymmetric instability of centrifugally stable stratified Taylor–Couette flow. J. Fluid Mech. 448, 1–21.CrossRefGoogle Scholar