Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-20T04:56:44.918Z Has data issue: false hasContentIssue false
  • English
  • Français

Stratified Ekman layers evolving under a finite-time stabilizing buoyancy flux

Published online by Cambridge University Press:  12 February 2018

S. M. Iman Gohari  and
Sutanu Sarkar Open the ORCID record for Sutanu Sarkar [Opens in a new window]
S. M. Iman Gohari
Affiliation:
Department of Mechanical and Aerospace Engineering, University of California at San Diego, La Jolla, CA 92093-0411, USA
Sutanu Sarkar*
Affiliation:
Department of Mechanical and Aerospace Engineering, University of California at San Diego, La Jolla, CA 92093-0411, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Stratified flow in nocturnal boundary layers is studied using direct numerical simulation (DNS) of the Ekman layer, a model problem that is useful to understand atmospheric boundary-layer (ABL) turbulence. A stabilizing buoyancy flux is applied for a finite time to a neutral Ekman layer. Based on previous studies and the simulations conducted here, the choice of 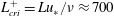$L_{\mathit{cri}}^{+}=Lu_{\ast }/\unicode[STIX]{x1D708}\approx 700$ (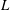$L$ is the Obukhov length scale and 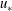$u_{\ast }$ is the friction velocity) provides a cooling flux that is sufficiently strong to cause the initial collapse of turbulence. The turbulent kinetic energy decays over a time scale of 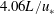$4.06L/u_{\ast }$ during the collapse. The simulations suggest that imposing 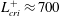$L_{\mathit{cri}}^{+}\approx 700$ on the neutral Ekman layer results in turbulence collapse during the initial transient, independent of Reynolds number, 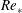$Re_{\ast }$. However, the long-time state of the flow, i.e. turbulent with spatial intermittency or non-turbulent, is found to depend on the initial value of 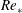$Re_{\ast }$ since the cooling flux and resultant stratification increase with 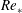$Re_{\ast }$ for a given 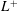$L^{+}$. The lower-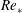$Re_{\ast }$ cases have sustained turbulence with shear and stratification profiles that evolve in a manner such that the gradient Richardson number, 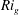$Ri_{g}$, in the near-surface layer, including the low-level jet, remains subcritical. The highest 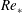$Re_{\ast }$ case has supercritical 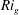$Ri_{g}$ in the low-level jet and turbulence does not recover. A theoretical discussion is performed to infer that the bulk Richardson number, 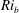$Ri_{b}$, is more suitable than 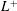$L^{+}$ to determine the fate of stratified Ekman layers at late time. DNS results support the implications of 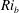$Ri_{b}$ for the effect of initial 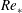$Re_{\ast }$ and 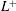$L^{+}$ on the flow.

JFM classification

Geophysical and Geological Flows: Atmospheric flows Geophysical and Geological Flows: Stratified flows Turbulent Flows: Stratified turbulence
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 840 , 10 April 2018 , pp. 266 - 290
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ansorge, C. & Mellado, J. P. 2014 Global intermittency and collapsing turbulence in the stratified planetary boundary layer. Boundary-Layer Meteorol. 153 (1), 89–116.Google Scholar
Ansorge, C. & Mellado, J. P. 2016 Analyses of external and global intermittency in the logarithmic layer of Ekman flow. J. Fluid Mech. 805, 611–635.Google Scholar
Armenio, V. & Sarkar, S. 2002 An investigation of stably-stratified channel flow using large eddy simulation. J. Fluid Mech. 459, 1–42.Google Scholar
Banta, R. M., Mahrt, L., Vickers, D., Sun, J., Balsley, B. B., Pichugina, Y. L. & Williams, E. J. 2007 The very stable boundary layer on nights with weak low-level jets. J. Atmos. Sci. 64, 3068–3090.Google Scholar
Bernardini, M., Pirozzoli, S. & Orlandi, P. 2014 Velocity statistics in turbulent channel flow up to Re𝜏 = 4000. J. Fluid Mech. 742, 171–191.CrossRefGoogle Scholar
Brethouwer, G., Billant, P., Lindborg, E. & Chomaz, J. 2007 Scaling analysis and simulation of strongly stratified turbulent flows. J. Fluid Mech. 585, 343–368.Google Scholar
Coleman, G. N., Ferziger, J. H. & Spalart, P. R. 1990 A numerical study of the turbulent Ekman layer. J. Fluid Mech. 213, 313–348.Google Scholar
Cuxart, J. & Jiménez, M. A. 2007 Mixing processes in a nocturnal low-level jet: an LES study. J. Atmos. Sci. 64, 1666–1679.CrossRefGoogle Scholar
Deusebio, E., Brethouwer, G., Schlatter, P. & Lindborg, E. 2014 A numerical study of the unstratified and stratified Ekman layer. J. Fluid Mech. 755, 672–704.CrossRefGoogle Scholar
Deusebio, E., Caulfield, C. P. & Taylor, J. R. 2015 The intermittency boundary in stratified plane couette flow. J. Fluid Mech. 781, 298–329.Google Scholar
Flores, O. & Riley, J. J. 2011 Analysis of turbulence collapse in the stably stratified surface layer using direct numerical simulation. Boundary-Layer Meteorol. 139 (2), 241–259.Google Scholar
Garcia-Villalba, M. & del Alamo, J. C. 2011 Turbulence modification by stable stratification in channel flow. Phys. Fluids 23 (4), 045104.CrossRefGoogle Scholar
Gohari, S. M. I. & Sarkar, S. 2017 Direct numerical simulation of turbulence collapse and rebirth in stably stratified Ekman flow. Boundary-Layer Meteorol. 162 (3), 401–426.Google Scholar
Hultmark, M., Vallikivi, M., Bailey, S. C. C. & Smits, A. J. 2012 Turbulent pipe flow at extreme Reynolds numbers. Phys. Rev. Lett. 108 (9), 094501.Google Scholar
Jacobitz, F. G., Sarkar, S. & Vanatta, C. W. 1997 Direct numerical simulations of the turbulence evolution in a uniformly sheared and stably stratified flow. J. Fluid Mech. 342, 231–261.Google Scholar
Jalali, M., Rapaka, N. R. & Sarkar, S. 2014 Tidal flow over topography: effect of excursion number on wave energetics and turbulence. J. Fluid Mech. 750, 259–283.Google Scholar
Nieuwstadt, F. T. M. 2005 Direct numerical simulation of stable channel flow at large stability. Boundary-Layer Meteorol. 116 (2), 277–299.Google Scholar
Pirozzoli, S., Bernardini, M. & Orlandi, P. 2014 Turbulence statistics in couette flow at high Reynolds number. J. Fluid Mech. 758, 327–343.Google Scholar
Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.Google Scholar
Poulos, G. S., Blumen, W., Fritts, D. C., Lundquist, J. K., Sun, J., Burns, S. P., Nappo, C., Banta, R., Newsom, R., Cuxart, J., Terradellas, E. et al. 2002 CASES-99: A comprehensive investigation of the stable nocturnal boundary layer. Bull. Am. Meteorol. Soc. 83 (4), 555–581.Google Scholar
Shah, S. K. & Bou-Zeid, E. 2014 Direct numerical simulations of turbulent Ekman layers with increasing static stability: modifications to the bulk structure and second-order statistics. J. Fluid Mech. 760, 494–539.Google Scholar
Shingai, K. & Kawamura, H. 2004 A study of turbulence structure and large-scale motion in the Ekman layer through direct numerical simulations. J. Turbul. 5, N13.Google Scholar
Smyth, W. D. & Moum, J. N. 2000 Length scales of turbulence in stably stratified mixing layers. Phys. Fluids 12 (6), 1327–1342.Google Scholar
Spalart, P. R., Coleman, G. N. & Johnstone, R. 2008 Direct numerical simulation of the Ekman layer: A step in Reynolds number, and cautious support for a log law with a shifted origin. Phys. Fluids 20 (10), 101507.CrossRefGoogle Scholar
Williams, O., Hohman, T., Van Buren, T., Bou-Zeid, E. & Smits, A. J. 2017 The effect of stable thermal stratification on turbulent boundary layer statistics. J. Fluid Mech. 812, 1039–1075.Google Scholar