Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-23T00:07:54.719Z Has data issue: false hasContentIssue false
  • English
  • Français

Stokes drift: theory and experiments

Published online by Cambridge University Press:  05 December 2019

Stephen G. Monismith
Stephen G. Monismith*
Affiliation:
Bob and Norma Street Environmental Fluid Mechanics Laboratory, Stanford, CA94305-4020, USA
*
†Email address for correspondence: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

An important facet of water wave dynamics is the fact that Stokes’ 1847 approximate theory of water waves predicts mean Lagrangian velocities even when mean Eulerian velocities are zero. This motion, known as Stokes drift, is important to a wide variety of oceanic processes. Reflecting the difficulty of avoiding effects associated with the boundaries in wave tanks, the first convincing experimental evidence confirming this behaviour has only recently been given in van den Bremer et al. (J. Fluid Mech., vol. 879, 2019, pp. 168–186). This is an important result given prior evidence that the exact rotational waves first studied by Gerstner in 1802 may exist. Nonetheless, despite more than 200 years of work on the theory of water waves, much remains to be discovered.

JFM classification

Waves/Free-surface Flows: Surface gravity waves
Type
Focus on Fluids
Information
Journal of Fluid Mechanics , Volume 884 , 10 February 2020 , F1
Copyright
© 2019 Cambridge University Press

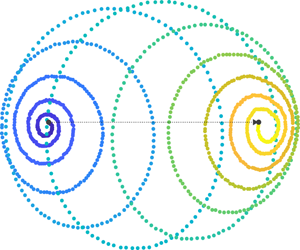
1 Introduction

While the theory of water waves has a long history (Craik Reference Craik2004), much of what is commonly used today is based on the seminal work of Sir Gabriel Stokes, first published in 1847 (Stokes Reference Stokes1847). In his analysis of irrotational water waves, Stokes formalized the approximation of the fully nonlinear boundary value problem by implicitly defining a solution that takes the form of a power series in wave steepness. Through this analysis he made a striking finding: while the time-averaged (mean) Eulerian velocity at any point in the fluid might be zero, there is a net motion of particles, i.e., a non-zero Lagrangian mean velocity, now known as the Stokes drift (e.g. Bühler Reference Bühler2014).

Stokes drift, which emerges as a property of the averaging of wave effects on the mean (wave averaged) flow, plays an important role in oceanic flows. For example, wave averaging the Navier–Stokes equations produces a body force acting on the mean velocity field that is proportional to the cross product of the mean vorticity and the Stokes drift (Craik & Leibovich Reference Craik and Leibovich1976). It is this ‘extra’ force that supports the instability that can produce Langmuir cells. Transport of materials in the ocean in the presence of waves is due to the Lagrangian mean velocity, the sum of the Stokes drift and the Eulerian mean velocity (e.g. Monismith & Fong Reference Monismith and Fong2004).

2 Overview

Given that the theory behind the Stokes drift is 172 years old, it is striking that the recent paper by van den Bremer et al. (Reference van den Bremer, Whittaker, Calvert, Raby and Taylor2019) is the first definitive, quantitative and unambiguous demonstration that the mean Lagrangian velocity in the absence of other flows can be accurately calculated from the lowest-order irrotational wave velocity field.

Why has it taken 172 years for experimental confirmation of Stokes’ theory to be made? It turns out that the experiment is surprisingly hard to do properly. The principal challenge is that the finite length of the tank, i.e., the existence of endwalls, forces a condition of no net flow through any cross-section, at least in steady state (Swan Reference Swan1990). In the absence of vorticity and of viscous effects, the Eulerian return flow required to balance the Stokes drift of a spatially uniform wave field should be independent of depth (van den Bremer et al. Reference van den Bremer, Whittaker, Calvert, Raby and Taylor2019). However, in the laboratory, as time proceeds, the mean Eulerian flow changes as the effects of sidewall, surface and bottom boundary layers begin to influence the flow in the interior of the tank (Longuet-Higgins Reference Longuet-Higgins1953). Moreover, how the waves are absorbed at the far end of the tank can also influence the flow in the interior (Swan Reference Swan1990; Swan & Sleath Reference Swan and Sleath1990). Thus, rather than using a constant wave field, it is preferable to use wave groups, as van den Bremer et al. (Reference van den Bremer, Whittaker, Calvert, Raby and Taylor2019) did, and thus to suitably modify the calculation of the Eulerian return flow, a flow that is driven by radiation stress gradients also associated with the mean set down of the group (Longuet-Higgins & Stewart Reference Longuet-Higgins and Stewart1962).

Focusing on the case where the group is long relative to the depth, van den Bremer et al. (Reference van den Bremer, Whittaker, Calvert, Raby and Taylor2019) express the leading-order Stokes drift and Eulerian return flow in terms of group properties, enabling them to convert measured free surface time series into predictions of the Lagrangian mean flow, expressed in terms of net displacements due to the passage of the group. As an aside, one interesting result of considering groups rather than steady waves is that the Stokes drift velocity is divergent. It also has a non-zero vertical component proportional to the rate of change with time of the group envelope amplitude, behaviour not found for steady wave fields, and which is considered contentious by McWilliams, Restrepo & Lane (Reference McWilliams, Restrepo and Lane2004).

Lagrangian particle tracks measured by van den Bremer et al. (Reference van den Bremer, Whittaker, Calvert, Raby and Taylor2019) show that displacements in both horizontal and vertical directions as the group passes through the measurement section can be predicted using Stokes’ theory. However, the most significant aspect of this work is the degree to which theory and particle tracking derived net motions match, despite the challenges of separating the wheat (net displacements due to wave passage that ranged from a few millimetres to several centimetres) from the chaff (seiching in the tank, eddies and vertical motions of the particles due to their small buoyancy). Thus, 172 years after Stokes’ seminal work, clear confirmation of his result for net motions under irrotational water waves has at last been given!

3 Future

The results in van den Bremer et al. (Reference van den Bremer, Whittaker, Calvert, Raby and Taylor2019) may not be the last word on this topic. In 1802 Gerstner used the Lagrangian momentum equations to derive an exact solution to the inviscid water wave problem valid up to and including the deformed free surface (Gerstner Reference Gerstner1802). These waves, known as Gerstner waves, closely resemble finite-amplitude Stokes waves, with the principal (and likely only observable) difference being that particle orbits are closed so that there is a rotational Eulerian mean flow that exactly cancels the lowest-order Stokes drift (Kinsman Reference Kinsman1965).

The problem with Gerstner’s surface waves is that they cannot be generated by conservative forces (Lamb Reference Lamb1932), and so should not be expected to arise in nature. However, there is evidence that the Stokes drift cancellation as described by Gerstner has been observed in the lab (Monismith et al. Reference Monismith, Cowen, Nepf, Magnaudet and Thais2007). The most striking example of this behaviour is the observation of mean Lagrangian flows under waves in the ocean reported by Smith (Reference Smith2006): as wave groups passed by his instruments, the mean Lagrangian velocity beneath them did not measurably change, exactly the behaviour that would be expected for Gerstner waves. However, while shallow water velocity measurements reported by Lentz et al. (Reference Lentz, Fewings, Howd, Fredericks and Hathaway2008) also showed Stokes drift cancellation, this behaviour can be attributed to the vortex force associated with the product of the planetary vorticity and the Stokes drift, a result first predicted by Ursell (Reference Ursell1950) for steady waves in an infinite ocean.

Thus, a central question that remains is: under what circumstances, if any, can Gerstner waves arise? For example, it is possible that since Gerstner waves involve vorticity, surface waves on underlying flows with some vorticity distributions might be Gerstner-like. However, unlike irrotational waves for which a variety of solutions to initial value problems involving wave generation are known (e.g. Stoker Reference Stoker1992), no such solutions have been found for Gerstner waves. In this regard, the recent work of Abrashkin (Reference Abrashkin2019) in which he appears to have derived a solution for unsteady Gerstner waves forced by spatially variable pressure forces clearly deserves further attention.

In conclusion, the experiments of van den Bremer et al. (Reference van den Bremer, Whittaker, Calvert, Raby and Taylor2019) show that the Stokes drift, mean motions predicted nearly two centuries ago, can take the form predicted by irrotational wave theory as Stokes first showed. Nonetheless, the fact that wave behaviour outside of what Stokes predicted may also exist also shows that, despite nearly two centuries of study since Stokes’ foundational paper, interesting problems in water wave mechanics remain to be solved both through new theory and innovative experiments like those of van den Bremer et al.

References

Abrashkin, A. 2019 Unsteady Gerstner waves. Chaos, Solitons Fractals 118, 152–158.CrossRefGoogle Scholar
van den Bremer, T. S., Whittaker, C., Calvert, R., Raby, A. & Taylor, P. H. 2019 Experimental study of particle trajectories below deep-water surface gravity wave groups. J. Fluid Mech. 879, 168–186.CrossRefGoogle Scholar
Bühler, O. 2014 Waves and Mean Flows, 2nd edn. Cambridge University Press.CrossRefGoogle Scholar
Craik, A. D. D. 2004 The origins of water wave theory. Annu. Rev. Fluid Mech. 36, 1–28.CrossRefGoogle Scholar
Craik, A. D. D. & Leibovich, S. 1976 A rational model for Langmuir circulations. J. Fluid Mech. 73, 401–426.CrossRefGoogle Scholar
Gerstner, F. J.1802 Theorie der Wellen. Abh. König. Böhm. Ges. Wiss.; (Reprinted in: Ann. Phys. 32, 412–445 (1809)).Google Scholar
Kinsman, B. 1965 Wind Waves: Their Generation and Propagation on the Ocean’s Surface. Prentice-Hall.Google Scholar
Lamb, H. 1932 Hydrodynamics. Cambridge University Press.Google Scholar
Lentz, S. J., Fewings, M., Howd, P., Fredericks, J. & Hathaway, K. 2008 Observations and a model of undertow over the inner continental shelf. J. Phys. Oceanogr. 38, 2341–2357.CrossRefGoogle Scholar
Longuet-Higgins, M. S. 1953 Mass transport in water waves. Phil. Trans. R. Soc. Lond. A 245, 535–581.CrossRefGoogle Scholar
Longuet-Higgins, M. S. & Stewart, R. W. 1962 Radiation stress and mass transport in gravity waves, with applications to ‘surf beats’. J. Fluid Mech. 13, 481–504.Google Scholar
McWilliams, J. C., Restrepo, J. M. & Lane, E. M. 2004 An asymptotic theory for the interaction of waves and currents in coastal waters. J. Fluid Mech. 511, 135–178.Google Scholar
Monismith, S. G., Cowen, E. A., Nepf, H. M., Magnaudet, J. & Thais, L. 2007 Laboratory observations of mean flows under surface gravity waves. J. Fluid Mech. 573, 131–147.Google Scholar
Monismith, S. G. & Fong, D. A. 2004 A note on the potential transport of scalars and organisms by surface waves. Limnol. Oceanogr. 49, 1214–1217.Google Scholar
Smith, J. A. 2006 Observed variability of ocean wave Stokes drift, and the Eulerian response to passing groups. J. Phys. Oceanogr. 36, 1381–1402.CrossRefGoogle Scholar
Stoker, J. 1992 Water Waves. Wiley.CrossRefGoogle Scholar
Stokes, G. G. 1847 On the theory of oscillatory waves. Trans. Camb. Phil. Soc. 8, 441–455.Google Scholar
Swan, C. 1990 Convection within an experimental wave flume. J. Hydraul. Res. 28, 273–282.CrossRefGoogle Scholar
Swan, C. & Sleath, J. F. A. 1990 A second approximation to the time-mean Lagrangian drift beneath progressive gravity waves. Ocean Engng 1, 65–79.CrossRefGoogle Scholar
Ursell, F. 1950 On the theoretical form of ocean swell on a rotating earth. Mon. Not. R. Astron. Soc. Geophys. Suppl. 6, 1–8.CrossRefGoogle Scholar