Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-28T21:41:38.987Z Has data issue: false hasContentIssue false
  • English
  • Français

Stimulated generation: extraction of energy from balanced flow by near-inertial waves

Published online by Cambridge University Press:  23 May 2018

Cesar B. Rocha Open the ORCID record for Cesar B. Rocha [Opens in a new window] ,
Gregory L. Wagner Open the ORCID record for Gregory L. Wagner [Opens in a new window]  and
William R. Young Open the ORCID record for William R. Young [Opens in a new window]
Cesar B. Rocha*
Affiliation:
Scripps Institution of Oceanography, University of California, San Diego, USA
Gregory L. Wagner
Affiliation:
Department of Earth, Atmospheric and Planetary Sciences, Massachusetts Institute of Technology, USA
William R. Young
Affiliation:
Scripps Institution of Oceanography, University of California, San Diego, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We study stimulated generation – the transfer of energy from balanced flows to existing internal waves – using an asymptotic model that couples barotropic quasi-geostrophic flow and near-inertial waves with 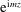$\text{e}^{\text{i}mz}$ vertical structure, where 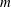$m$ is the vertical wavenumber and $z$ is the vertical coordinate. A detailed description of the conservation laws of this vertical-plane-wave model illuminates the mechanism of stimulated generation associated with vertical vorticity and lateral strain. There are two sources of wave potential energy, and corresponding sinks of balanced kinetic energy: the refractive convergence of wave action density into anti-cyclones (and divergence from cyclones); and the enhancement of wave-field gradients by geostrophic straining. We quantify these energy transfers and describe the phenomenology of stimulated generation using numerical solutions of an initially uniform inertial oscillation interacting with mature freely evolving two-dimensional turbulence. In all solutions, stimulated generation co-exists with a transfer of balanced kinetic energy to large scales via vortex merging. Also, geostrophic straining accounts for most of the generation of wave potential energy, representing a sink of 10 %–20 % of the initial balanced kinetic energy. However, refraction is fundamental because it creates the initial eddy-scale lateral gradients in the near-inertial field that are then enhanced by advection. In these quasi-inviscid solutions, wave dispersion is the only mechanism that upsets stimulated generation: with a barotropic balanced flow, lateral straining enhances the wave group velocity, so that waves accelerate and rapidly escape from straining regions. This wave escape prevents wave energy from cascading to dissipative scales.

JFM classification

Geophysical and Geological Flows: Internal waves Geophysical and Geological Flows: Ocean processes Geophysical and Geological Flows: Quasi-geostrophic flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 847 , 25 July 2018 , pp. 417 - 451
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Balmforth, N. J., Llewellyn Smith, S. G. & Young, W. R. 1998 Enhanced dispersion of near-inertial waves in an idealized geostrophic flow. J. Mar. Res. 56 (1), 1–40.Google Scholar
Balmforth, N. J. & Young, W. R. 1999 Radiative damping of near-inertial oscillations in the mixed layer. J. Mar. Res. 57 (4), 561–584.Google Scholar
Barkan, R., Winters, K. B. & McWilliams, J. C. 2016 Stimulated imbalance and the enhancement of eddy kinetic energy dissipation by internal waves. J. Phys. Oceanogr. 47, 181–198.CrossRefGoogle Scholar
Bretherton, F. P. & Garrett, C. J. R. 1968 Wavetrains in inhomogeneous moving media. Proc. R. Soc. Lond. A 302, 529–554.Google Scholar
Bühler, O. & McIntyre, M. E. 1998 On non-dissipative wave–mean interactions in the atmosphere or oceans. J. Fluid Mech. 354, 301–343.Google Scholar
Bühler, O. & McIntyre, M. E. 2005 Wave capture and wave–vortex duality. J. Fluid Mech. 534, 67–95.Google Scholar
Cox, S. M. & Matthews, P. C. 2002 Exponential time differencing for stiff systems. J. Comput. Phys. 176 (2), 430–455.CrossRefGoogle Scholar
Danioux, E., Vanneste, J. & Bühler, O. 2015 On the concentration of near-inertial waves in anticyclones. J. Fluid Mech. 773, R2.CrossRefGoogle Scholar
Danioux, E., Vanneste, J., Klein, P. & Sasaki, H. 2012 Spontaneous inertia-gravity-wave generation by surface-intensified turbulence. J. Fluid Mech. 699, 153–157.Google Scholar
Fornberg, B. 1977 A numerical study of 2-D turbulence. J. Comput. Phys. 25 (1), 1–31.CrossRefGoogle Scholar
Gertz, A. & Straub, D. N. 2009 Near-inertial oscillations and the damping of midlatitude gyres: a modeling study. J. Phys. Oceanogr. 39 (9), 2338–2350.CrossRefGoogle Scholar
Grimshaw, R. 1975 Nonlinear internal gravity waves in a rotating fluid. J. Fluid Mech. 71 (3), 497–512.Google Scholar
Hoskins, B. J. 1975 The geostrophic momentum approximation and the semi-geostrophic equations. J. Atmos. Sci. 32 (2), 233–242.2.0.CO;2>CrossRefGoogle Scholar
Kassam, A.-K. & Trefethen, L. N. 2005 Fourth-order time-stepping for stiff PDEs. SIAM J. Sci. Comput. 26 (4), 1214–1233.CrossRefGoogle Scholar
Klein, P., Llewellyn Smith, S. G. & Lapeyre, G. 2004 Organization of near-inertial energy by an eddy field. Q. J. R. Meteorol. Soc. 130 (598), 1153–1166.Google Scholar
Landau, L. D. & Lifshitz, E. M. 2013 Quantum Mechanics: Non-relativistic Theory, vol. 3. Elsevier.Google Scholar
McIntyre, M. E. 2009 Spontaneous imbalance and hybrid vortex–gravity structures. J. Atmos. Sci. 66 (5), 1315–1326.CrossRefGoogle Scholar
McWilliams, J. C. 1984 The emergence of isolated coherent vortices in turbulent flow. J. Fluid Mech. 146, 21–43.Google Scholar
Meleshko, V. V. & Van Heijst, G. J. F. 1994 On Chaplygin’s investigations of two-dimensional vortex structures in an inviscid fluid. J. Fluid Mech. 272, 157–182.CrossRefGoogle Scholar
Moehlis, J. & Llewellyn Smith, S. G. 2001 Radiation of mixed layer near-inertial oscillations into the ocean interior. J. Phys. Oceanogr. 31 (6), 1550–1560.2.0.CO;2>CrossRefGoogle Scholar
Muraki, D. J., Snyder, C. & Rotunno, R. 1999 The next-order corrections to quasigeostrophic theory. J. Atmos. Sci. 56 (11), 1547–1560.Google Scholar
Nagai, T., Tandon, A., Kunze, E. & Mahadevan, A. 2015 Spontaneous generation of near-inertial waves by the Kuroshio Front. J. Phys. Oceanogr. 45 (9), 2381–2406.Google Scholar
Salmon, R. 2016 Variational treatment of inertia-gravity waves interacting with a quasigeostrophic mean flow. J. Fluid Mech. 809, 502–529.Google Scholar
Shakespeare, C. J. & Hogg, A. McC. 2017 Spontaneous surface generation and interior amplification of internal waves in a regional-scale ocean model. J. Phys. Oceanogr. 46 (7), 2063–2081.Google Scholar
Taylor, S. & Straub, D. N. 2016 Forced near-inertial motion and dissipation of low-frequency kinetic energy in a wind-driven channel flow. J. Phys. Oceanogr. 46 (1), 79–93.Google Scholar
Thomas, L. N. 2012 On the effects of frontogenetic strain on symmetric instability and inertia-gravity waves. J. Fluid Mech. 711, 620–640.Google Scholar
Vanneste, J. 2013 Balance and spontaneous wave generation in geophysical flows. Annu. Rev. Fluid Mech. 45, 147–172.Google Scholar
Wagner, G. L. & Young, W. R. 2015 Available potential vorticity and wave-averaged quasi-geostrophic flow. J. Fluid Mech. 785, 401–424.Google Scholar
Wagner, G. L. & Young, W. R. 2016 A three-component model for the coupled evolution of near-inertial waves, quasi-geostrophic flow and the near-inertial second harmonic. J. Fluid Mech. 802, 806–837.CrossRefGoogle Scholar
Xie, J.-H. & Vanneste, J. 2015 A generalised-Lagrangian-mean model of the interactions between near-inertial waves and mean flow. J. Fluid Mech. 774, 143–169.CrossRefGoogle Scholar
Young, W. R. & Ben Jelloul, M. 1997 Propagation of near-inertial oscillations through a geostrophic flow. J. Mar. Res. 55 (4), 735–766.Google Scholar
Young, W. R., Rhines, P. B. & Garrett, C. J. R. 1982 Shear-flow dispersion, internal waves and horizontal mixing in the ocean. J. Phys. Oceanogr. 12 (6), 515–527.Google Scholar