Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-17T15:17:08.411Z Has data issue: false hasContentIssue false
  • English
  • Français

Stereo-PIV measurements of spatio-temporal turbulence correlations in an axisymmetric jet

Published online by Cambridge University Press:  30 July 2015

C. D. Pokora  and
J. J. McGuirk
C. D. Pokora
Affiliation:
Department of Aeronautical and Automotive Engineering, Loughborough University, Loughborough, Leicestershire LE11 3TU, UK
J. J. McGuirk*
Affiliation:
Department of Aeronautical and Automotive Engineering, Loughborough University, Loughborough, Leicestershire LE11 3TU, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Stereoscopic three-component particle image velocimetry (3C-PIV) measurements have been made in a turbulent round jet to investigate the spatio-temporal correlations that are the origin of aerodynamic noise. Restricting attention to subsonic, isothermal jets, measurements were taken in a water flow experiment where, for the same Reynolds number and nozzle size, the shortest time scale of the dynamically important turbulent structures is more than an order of magnitude greater that in equivalent airflow experiments, greatly facilitating time-resolved PIV measurements. Results obtained (for a jet nozzle diameter and velocity of 40 mm and 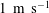$1~\text{m}~\text{s}^{-1}$, giving 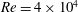$\mathit{Re}=4\times 10^{4}$) show that, on the basis of both single-point statistics and two-point quantities (correlation functions, integral length scales) the present incompressible flow data are in excellent agreement with published compressible, subsonic airflow measurements. The 3C-PIV data are first compared to higher-spatial-resolution 2C-PIV data and observed to be in good agreement, although some deterioration in quality for higher-order correlations caused by high-frequency noise in the 3C-PIV data is noted. A filter method to correct for this is proposed, based on proper orthogonal decomposition (POD) of the 3C-PIV data. The corrected data are then used to construct correlation maps at the second- and fourth-order level for all velocity components. The present data are in accordance with existing hot-wire measurements, but provide significantly more detailed information on correlation components than has previously been available. The measured relative magnitudes of various components of the two-point fourth-order turbulence correlation coefficient (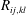$R_{ij,kl}$) – the fundamental building block for free shear flow aerodynamic noise sources – are presented and represent a valuable source of validation data for acoustic source modelling. The relationship between fourth-order and second-order velocity correlations is also examined, based on an assumption of a quasi-Gaussian nearly normal p.d.f. for the velocity fluctuations. The present results indicate that this approximation shows reasonable agreement for the measured relative magnitudes of several correlation components; however, areas of discrepancy are identified, indicating the need for work on alternative models such as the shell turbulence concept of Afsar (Eur. J. Mech. (B/Fluids), vol. 31, 2012, pp. 129–139).

JFM classification

Wakes/Jets: Jets Turbulent Flows: Shear layer turbulence Turbulent Flows: Turbulent Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 778 , 10 September 2015 , pp. 216 - 252
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

‡

Present address: Tata Technologies, Bristol BS16 1EJ, UK.

References

Afsar, M. Z. 2012 Insight into the two-source structure of the jet noise spectrum using a generalised shell model of turbulence. Eur. J. Mech. (B/Fluids) 31, 129–139.Google Scholar
Alkislar, M. B. 2007 Correction of turbulence quantities in 3D PIV data. In AIAA 2007-526, 45th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA.Google Scholar
Alkislar, M. B., Krothapalli, A. & Butler, G. W. 2007 The effect of streamwise vortices on the aeroacoustics of a Mach 0.9 jet. J. Fluid Mech. 578, 139–169.CrossRefGoogle Scholar
Batchelor, G. K. 1953 The Theory of Homogeneous Turbulence. Cambridge University Press.Google Scholar
Behrouzi, P. & McGuirk, J. J. 2004 Jet mixing enhancement using fluid tabs. In AIAA 2004-2401, 2nd AIAA Flow Control Conference, Portland, OR, USA.Google Scholar
Behrouzi, P. & McGuirk, J. J. 2006 Effect of tab parameters on near-field jet plume development. AIAA J. Propul. Power 22, 576–583.Google Scholar
Bradshaw, P., Ferris, D. H. & Johnson, R. F. 1964 Turbulence in the noise producing region of a circular jet. J. Fluid Mech. 19, 591–621.Google Scholar
Bridges, J. & Wernet, M. 2003 Measurements of the aeroacoustic sound source in hot jets. In AIAA 2003-3130, 9th AIAA/CEAS Aeroacoustics Conference, Hilton Head, SC, USA.Google Scholar
Bridges, J. & Wernet, M. 2010 Establishing consensus turbulence statistics for hot subsonic jets. In AIAA 2010-3751, 16th AIAA/CEAS Aeroacoustics Conference, Stockholm, Sweden.Google Scholar
Bridges, J. & Wernet, M. 2012 Validating Large Eddy Simulation for jet aeroacoustics. AIAA J. Propul. Power 28, 226–234.Google Scholar
Chatellier, L. & Fitzpatrick, J. 2005 Spatio-temporal correlation analysis of turbulent flows using global and single-point measurements. Exp. Fluids 38, 563–575.Google Scholar
Craya, A. & Curtet, R. 1955 On the spreading of a confined jet. C. R. Acad. Sci. Paris 241, 621–622.Google Scholar
Davies, P. O. A. L., Fisher, M. J. & Barratt, M. J. 1962 The characteristics of the turbulence in the mixing region of a round jet. J. Fluid Mech. 15, 337–367.Google Scholar
Fellouah, H., Ball, C. G. & Pollard, A. 2009 Reynolds number effects within the development region of a turbulent round free jet. Intl J. Heat Mass Transfer 52, 3943–3954.Google Scholar
Fisher, M. J. & Davies, P. O. A. L. 1964 Correlation measurements in a non-frozen pattern of turbulence. J. Fluid Mech. 18, 97–116.CrossRefGoogle Scholar
Fleury, V., Bailly, C., Jondeau, E., Michard, M. & Juve, D. 2008 Space–time correlations in two subsonic jets using dual-PIV measurements. AIAA J. 46, 2498–2509.Google Scholar
Harper-Bourne, M. 1999 Jet near-field noise prediction. In AIAA 1999-3214, 5th AIAA/CEAS Aeroacoustics Conference, Seattle, WA, USA.Google Scholar
Harper-Bourne, M. 2003 Jet noise turbulence measurements. In AIAA 2003-3214, 9th AIAA/CEAS Aeroacoustics Conference, Hilton Head, SC, USA.Google Scholar
Hoest-Madsen, A. & Nielsen, A. H. 1995 Accuracy of PIV measurements in turbulent flows. In Laser Anemometry, vol. 229, pp. 481–488. American Society of Mechanical Engineers, New York, NY, USA.Google Scholar
Karabasov, S. A., Afsar, M. Z., Hynes, T. P., Dowling, A. P., McMullan, W. A., Pokora, C. D., Page, G. J. & McGuirk, J. J. 2010 Jet noise: acoustic analogy informed by Large Eddy Simulation. AIAA J. 48, 1312–1325.Google Scholar
Kerherve, F., Fitzpatrick, J. & Jordan, P. 2006 The frequency dependence of jet turbulence for jet noise modelling. J. Sound Vib. 296, 209–225.Google Scholar
Kerherve, F., Jordan, P., Gervais, Y., Valiere, J. C. & Braud, P. 2004 Two-point laser Doppler velocimetry measurements in a Mach 1.2 cold supersonic jet for statistical aeroacoustic source model. Exp. Fluids 37, 419–437.Google Scholar
Lau, J. C. 1980 Laser velocimeter correlation measurements in subsonic and supersonic jets. J. Sound Vib. 70, 85–101.Google Scholar
Lau, J. C., Morris, P. J. & Fisher, M. 1979 Measurements in subsonic and supersonic free jets using a laser velocimeter. J. Fluid Mech. 93, 1–27.Google Scholar
Laurence, J. C.1956 Intensity, scale, and spectra of turbulence in the mixing region of a free subsonic jet. NACA Tech. Rep. TN-1292.Google Scholar
Leib, S. J. & Goldstein, M. E. 2011 Hybrid source model for predicting high speed jet noise. AIAA J. 49, 1324–1335.Google Scholar
Liepmann, H. W. & Laufer, J.1947 Investigations of free turbulent mixing. NACA Tech. Rep. TN-1257.Google Scholar
Lighthill, M. J. 1952 On sound generated aerodynamically – I: general theory. Proc. R. Soc. Lond. A 211, 564–587.Google Scholar
Lighthill, M. J. 1954 On sound generated aerodynamically – II: turbulence as a source of sound. Proc. R. Soc. Lond. A 222, 1–32.Google Scholar
Lilley, G. M. 1958 On the noise from air jets. Aero. Res. Counc. R&M 20, 20–27.Google Scholar
Midgley, K., Spencer, A. & McGuirk, J. J. 2005 Unsteady flow structures in radial swirler fed fuel injectors. Trans. ASME: J. Engng Gas Turbines Power 127, 755–764.Google Scholar
Millionshchikov, M. D. 1941 On the theory of homogeneous isotropic turbulence. Dokl. Akad. Nauk SSSR 32, 611–614.Google Scholar
Morris, P. J. & Farassat, F. 2002 Acoustic analogy and alternate theories for jet noise prediction. AIAA J. 40, 671–680.CrossRefGoogle Scholar
Morris, P. J. & Zaman, K. B. M. Q. 2010 Velocity measurements in jets with application to noise source modelling. J. Sound Vib. 329, 394–414.CrossRefGoogle Scholar
Papamoschou, D. & Roshko, A. 1988 The compressible turbulent shear layer: an experimental study. J. Fluid Mech. 197, 453–477.Google Scholar
Pokora, C. D.2009 Spatio-temporal correlations of jets using high speed particle image velocimetry. PhD thesis, Loughborough University.Google Scholar
Pokora, C. D. & McGuirk, J. J. 2008 Spatio-temporal correlations using high-speed PIV in an axisymmetric jet. In AIAA 2008-3028, 14th AIAA/CEAS Aeroacoustic Conference, Vancouver, Canada.Google Scholar
Power, O., Kerherve, F., Fitzpatrick, J. & Jordan, P. 2004 Measurements of turbulence statistics in high subsonic jets. In AIAA 2004-3021, 10th AIAA/CEAS Aeroacoustics Conference, Manchester, UK.Google Scholar
Proudman, I. 1952 The generation of noise by isotropic turbulence. Proc. R. Soc. Lond. A 214, 119–132.Google Scholar
Ricou, F. & Spalding, D. B. 1961 Measurements of entrainment by axisymmetric turbulent jets. J. Fluid Mech. 11, 21–32.Google Scholar
Self, R. H. 2004 Jet noise prediction using the Lighthill acoustic analogy. J. Sound Vib. 275, 755–768.CrossRefGoogle Scholar
Spencer, A. & Hollis, D. 2005 Correcting for sub-grid filtering effects in particle image velocimetry data. Meas. Sci. Technol. 16, 2323–2335.CrossRefGoogle Scholar
Weitao, B., Yasuhiko, S. & Haruki, M. 2003 Time-resolved proper orthogonal decomposition of the near-field flow of a round jet measured by dynamic particle image velocimetry. Meas. Sci. Technol. 14, L1–L5.Google Scholar
Wernet, M. P. 2007 Temporally-resolved PIV for space–time correlations in both cold and hot jet flows. Meas. Sci. Technol. 18, 1387–1403.CrossRefGoogle Scholar
Westerweel, J., Draad, A. A., Van der Hoeven, J. G. T. & Van Oord, J. 1996 Measurement of fully-developed turbulent pipe flow with digital particle image velocimetry. Exp. Fluids 20, 165–177.Google Scholar