Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-06T00:54:35.676Z Has data issue: false hasContentIssue false
  • English
  • Français

Steady small-disturbance transonic dense gas flow past two-dimensional compression/expansion ramps

Published online by Cambridge University Press:  13 June 2018

A. Kluwick  and
E. A. Cox Open the ORCID record for E. A. Cox [Opens in a new window]
A. Kluwick*
Affiliation:
Institute of Fluid Dynamics and Heat Transfer, Vienna University of Technology, Tower BA/E322, Getreidemarkt 9, 1060 Vienna, Austria
E. A. Cox
Affiliation:
School of Mathematics and Statistics, Science Centre North, University College Dublin, Belfield, Dublin 4, Ireland
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

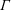The behaviour of steady transonic dense gas flow is essentially governed by two non-dimensional parameters characterising the magnitude and sign of the fundamental derivative of gas dynamics ($\unicode[STIX]{x1D6E4}$) and its derivative with respect to the density at constant entropy (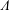$\unicode[STIX]{x1D6EC}$) in the small-disturbance limit. The resulting response to external forcing is surprisingly rich and studied in detail for the canonical problem of two-dimensional flow past compression/expansion ramps.

JFM classification

Compressible Flows: Compressible Flows Compressible Flows: Gas dynamics Compressible Flows: Shock waves
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 848 , 10 August 2018 , pp. 756 - 787
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alferez, N. & Touber, E. 2017 One-dimensional refraction properties of compression shocks in non-ideal gases. J. Fluid Mech. 814, 185–221.Google Scholar
Bates, J. W. & Montgomery, D. C. 1999 Some numerical studies of exotic shock wave behavior. Phys. Fluids 11, 462–474.CrossRefGoogle Scholar
Ben-Dor, G. 2007 Shock Wave Reflection Phenomena, 2nd edn. Springer.Google Scholar
Bethe, H. A.1942 The theory of shock waves for an arbitrary equation of state. Tech. Rep. 545. Office of Scientific Research and Development.Google Scholar
Chandrasekar, D. & Prasad, P. 1991 Transonic flow of a fluid with positive and negative nonlinearity through a nozzle. Phys. Fluids A 3 (3), 427–438.Google Scholar
Chen, G.-Q. 2017 Supersonic flow onto solid wedges, multidimensional shock waves and free boundary problems. Sci. China (Mathematics) 60 (9), 1–19.Google Scholar
Cole, J. D. & Cook, L. P. 1986 Transonic Aerodynamics. North Holland.Google Scholar
Colonna, P., Guardone, A. & Nannan, N. R. 2007 Siloxanes: a new class of candidate Bethe–Zel’dovich–Thompson fluids. Phys. Fluids 19, 086102.CrossRefGoogle Scholar
Courant, R. & Friedrichs, K. O. 1948 Supersonic Flow and Shock Waves. Interscience Publishers, Inc.Google Scholar
Cramer, M. S. & Kluwick, A. 1984 On the propagation of waves exhibiting both positive and negative nonlinearity. J. Fluid Mech. 142, 9–37.Google Scholar
Cramer, M. S. & Tarkenton, G. M. 1992 Transonic flows of Bethe–Zel’dovich–Thompson fluids. J. Fluid Mech. 240, 197–228.CrossRefGoogle Scholar
D’yakov, S. P. 1954 Shock wave stability. Zh. Eksp. Teor. Fiz. 27, 288–295.Google Scholar
Erpenbeck, J. J. 1962 Stability of Step Shocks. Phys. Fluids 5, 1181–1187.Google Scholar
Erpenbeck, J. J. 1963 Reply to comments by Gardner. Phys. Fluids 6, 1368.Google Scholar
Gardner, C. S. 1963 Comment on ‘stability of step shocks’. Phys. Fluids 6, 1366–1368.CrossRefGoogle Scholar
Gori, G., Vimercati, D. & Guardone, A. 2017 Non-ideal compressible-fluid effects in oblique shock waves. J. Phys.: Conf. Ser. 821, 012003.Google Scholar
Guardone, A., Colonna, P., Casati, E. & Rinaldi, E. 2014 Non-classical gas dynamics of vapour mixtures. J. Fluid Mech. 741, 681–701.Google Scholar
Guderley, K. G. 1957 Theorie schallnaher Strömungen. Springer, Trans. by J. R. Moszynski, Pergamon Press, 1962.Google Scholar
Kluwick, A. 1991 Small-amplitude finite-rate waves in fluids having both positive and negative nonlinearity. In Nonlinear Waves in Real Fluids (ed. Kluwick, A.), International Centre for Mechanical Sciences, vol. 315, pp. 1–43. Springer.CrossRefGoogle Scholar
Kluwick, A. 1993 Transonic nozzle flow of dense gases. J. Fluid Mech. 247, 661–688.Google Scholar
Kluwick, A. 2001 Theory of shock waves. rarefaction shocks. In Handbook of Shockwaves (ed. Ben-Dor, G., Igra, O., Elperin, T. & Lifshitz, A.), vol. 1, pp. 339–411. Academic Press.Google Scholar
Kraiko, A. N., P’yankov, K. S. & Yakovlev, Y. A. 2014 The flow of a supersonic ideal gas with ‘weak’ and ‘strong’ shocks over a wedge. Z. Angew. Math. Mech. 78, 318–330.Google Scholar
Monaco, J. F., Cramer, M. S. & Watson, L. T. 1997 Supersonic flows of dense gases in cascade configurations. J. Fluid Mech. 330, 31–59.Google Scholar
Richter, H. 1948 Die Stabilität des Verdichtungsstoßes in einer konkaven Ecke. Z. Angew. Math. Mech. 28, 341–345.Google Scholar
Schnerr, G. H. & Molokov, S. 1994 Exact solutions for transonic flows of dense gases in two-dimensional and axisymmetric nozzles. Phys. Fluids 6 (10), 3465–3472.CrossRefGoogle Scholar
Thompson, P. A. 1971 A fundamental derivative in gasdynamics. Phys. Fluids 14 (9), 1843–1849.Google Scholar
Zel’dovich, Ya. B. 1946 On the possibility of rarefaction shock waves. Zh. Eksp. Teor. Fiz. 4, 363–364.Google Scholar