Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-26T20:10:35.945Z Has data issue: false hasContentIssue false
  • English
  • Français

The steady oblique path of buoyancy-driven disks and spheres

Published online by Cambridge University Press:  19 July 2012

David Fabre ,
Joël Tchoufag  and
Jacques Magnaudet
David Fabre
Affiliation:
Université de Toulouse; INPT, UPS; IMFT (Institut de Mécanique des Fluides de Toulouse); Allée Camille Soula, F-31400 Toulouse, France
Joël Tchoufag
Affiliation:
Université de Toulouse; INPT, UPS; IMFT (Institut de Mécanique des Fluides de Toulouse); Allée Camille Soula, F-31400 Toulouse, France
Jacques Magnaudet*
Affiliation:
Université de Toulouse; INPT, UPS; IMFT (Institut de Mécanique des Fluides de Toulouse); Allée Camille Soula, F-31400 Toulouse, France CNRS; IMFT; F-31400 Toulouse, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider the steady motion of disks of various thicknesses in a weakly viscous flow, in the case where the angle of incidence (defined as that between the disk axis and its velocity) is small. We derive the structure of the steady flow past the body and the associated hydrodynamic force and torque through a weakly nonlinear expansion of the flow with respect to . When buoyancy drives the body motion, we obtain a solution corresponding to an oblique path with a non-zero incidence by requiring the torque to vanish and the hydrodynamic and net buoyancy forces to balance each other. This oblique solution is shown to arise through a bifurcation at a critical Reynolds number which does not depend upon the body-to-fluid density ratio and is distinct from the critical Reynolds number 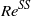corresponding to the steady bifurcation of the flow past the body held fixed with 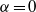. We then apply the same approach to the related problem of a sphere that weakly rotates about an axis perpendicular to its path and show that an oblique path sets in at a critical Reynolds number 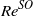slightly lower than 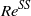, in agreement with available numerical studies.

JFM classification

Nonlinear Dynamical Systems: Bifurcation Aerodynamics: Flow-structure interactions Wakes/Jets: Wakes
Type
Papers
Information
Journal of Fluid Mechanics , Volume 707 , 25 September 2012 , pp. 24 - 36
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Assemat, P., Fabre, D. & Magnaudet, J. 2012 The onset of unsteadiness of two-dimensional bodies falling or rising freely in a viscous fluid: a linear study. J. Fluid Mech. 690, 173–202.CrossRefGoogle Scholar
2. Auguste, F. 2010 Instabilités de sillage générées derrière un corps solide cylindrique fixe ou mobile dans un fluide visqueux. PhD thesis, Université de Toulouse, France. Available online at https://www.imft.fr/Projet-ANR-OBLIC.Google Scholar
3. Chrust, M., Bouchet, G. & Dusek, J. 2010 Parametric study of the transition scenario in the wake of oblate spheroids and flat cylinders. J. Fluid Mech. 665, 199–208.CrossRefGoogle Scholar
4. Ern, P., Risso, F., Fabre, D. & Magnaudet, J. 2012 Wake-induced oscillatory paths of bodies freely rising or falling in fluids. Annu. Rev. Fluid Mech. 44, 97–121.CrossRefGoogle Scholar
5. Fabre, D., Assemat, P. & Magnaudet, J. 2011 A quasi-static approach to the stability of the path of heavy bodies falling within a viscous fluid. J. Fluids Struct. 27, 758–767.CrossRefGoogle Scholar
6. Fabre, D., Auguste, F. & Magnaudet, J. 2008 Bifurcation and symmetry breaking in the wake of axisymmetric bodies. Phys. Fluids 20, 051702.CrossRefGoogle Scholar
7. Fernandes, P. C., Risso, F., Ern, P. & Magnaudet, J. 2007 Oscillatory motion and wake instability of freely-rising axisymmetric bodies. J. Fluid Mech. 573, 479–502.CrossRefGoogle Scholar
8. Horowitz, M. & Williamson, C. H. K. 2010 The effect of Reynolds number on the dynamics and wakes of freely rising and falling spheres. J. Fluid Mech. 651, 251–294.CrossRefGoogle Scholar
9. Jenny, M., Dusek, J. & Bouchet, G. 2004 Instabilities and transition of a sphere falling or ascending freely in a Newtonian fluid. J. Fluid Mech. 508, 201–239.CrossRefGoogle Scholar
10. Meliga, P., Chomaz, J.-M. & Sipp, D. 2009 Global mode interaction and pattern selection in the wake of a disk: a weakly nonlinear expansion. J. Fluid Mech. 633, 159–189.CrossRefGoogle Scholar
11. Natarajan, R. & Acrivos, A. 1993 The instability of the steady flow past spheres and disks. J. Fluid Mech. 254, 323–344.CrossRefGoogle Scholar
12. Veldhuis, C. H. J. & Biesheuvel, A. 2007 An experimental study of the regimes of motion of spheres falling or ascending freely in a Newtonian fluid. Intl J. Multiphase Flow 33, 1074–1087.CrossRefGoogle Scholar