Article contents
Steady motion of Bingham liquid plugs in two-dimensional channels
Published online by Cambridge University Press: 12 December 2011
Abstract
We study numerically the steady creeping motion of Bingham liquid plugs in two-dimensional channels as a model of mucus behaviour during airway reopening in pulmonary airways. In addition to flow analysis related to propagation of the plug, the stress distribution on the wall is studied for better understanding of potential airway epithelial cell injury mechanisms. The yield stress behaviour of the fluid was implemented through a regularized constitutive equation. The capillary number, 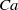 , and the Bingham number,
, and the Bingham number, 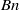 , which is the ratio of the yield stress to a characteristic viscous stress, varied over the ranges 0.025–0.1 and 0–1.5, respectively. For the range of parameters studied, it was found that, while the yield stress reduces the magnitude of the shearing along the wall, it can magnify the amplitude of the wall shear stress gradient significantly, and also it can elevate the magnitude of the wall shear stress and wall pressure gradient up to 30 % and 15 %, respectively. Therefore, the motion of mucus plugs can be more damaging to the airway epithelial cells due to the yield stress properties of mucus. The yield stress also modifies the profile of the plug where the amplitude of the capillary waves at the leading meniscus decreases with increase in
, which is the ratio of the yield stress to a characteristic viscous stress, varied over the ranges 0.025–0.1 and 0–1.5, respectively. For the range of parameters studied, it was found that, while the yield stress reduces the magnitude of the shearing along the wall, it can magnify the amplitude of the wall shear stress gradient significantly, and also it can elevate the magnitude of the wall shear stress and wall pressure gradient up to 30 % and 15 %, respectively. Therefore, the motion of mucus plugs can be more damaging to the airway epithelial cells due to the yield stress properties of mucus. The yield stress also modifies the profile of the plug where the amplitude of the capillary waves at the leading meniscus decreases with increase in  . Other findings are that: the thickness of the static film increases with increasing
. Other findings are that: the thickness of the static film increases with increasing 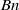 ; the driving pressure difference increases linearly with
; the driving pressure difference increases linearly with 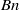 ; and increasing
; and increasing 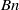 extends any wall stagnation point beneath the leading meniscus to an unyielded line segment beneath the leading meniscus. With an increase in
extends any wall stagnation point beneath the leading meniscus to an unyielded line segment beneath the leading meniscus. With an increase in 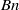 , the unyielded areas appear and grow in the adjacent wall film as well as the core region of the plug between the two menisci. The plug length,
, the unyielded areas appear and grow in the adjacent wall film as well as the core region of the plug between the two menisci. The plug length, 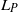 , mostly modifies the topology of the yield surfaces. It was found that the unyielded area in the core region between the two menisci grows as the plug length decreases. The very short Bingham plug behaves like a solid lamella. In all computed liquid plugs moving steadily, the von Mises stress attains its maximum value near the interface of the leading meniscus in the transition region. For Bingham plugs moving very slowly,
, mostly modifies the topology of the yield surfaces. It was found that the unyielded area in the core region between the two menisci grows as the plug length decreases. The very short Bingham plug behaves like a solid lamella. In all computed liquid plugs moving steadily, the von Mises stress attains its maximum value near the interface of the leading meniscus in the transition region. For Bingham plugs moving very slowly, 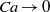 , the driving pressure is non-zero.
, the driving pressure is non-zero.
- Type
- Papers
- Information
- Journal of Fluid Mechanics , Volume 705: Special issue dedicated to Professor T. J. Pedley on his 70th birthday , 25 August 2012 , pp. 258 - 279
- Copyright
- Copyright © Cambridge University Press 2011
References
- 30
- Cited by


