Article contents
Steady approach of unsteady low-Reynolds-number flow past two rotating circular cylinders
Published online by Cambridge University Press: 07 November 2013
Abstract
The long-time viscous flow about two identical rotating circular cylinders in a side-by-side arrangement is investigated using an adaptive numerical scheme based on the vortex method. The Stokes solution of the steady flow about the two-cylinder cluster produces a uniform stream in the far field, which is the so-called Jeffery’s paradox. The present work first addresses the validation of the vortex method for a low-Reynolds-number computation. The unsteady flow past an abruptly started purely rotating circular cylinder is therefore computed and compared with an exact solution to the Navier–Stokes equations. The steady state is then found to be obtained for 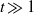 $t\gg 1$ with
$t\gg 1$ with 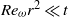 ${\mathit{Re}}_{\omega } {r}^{2} \ll t$, where the characteristic length and velocity are respectively normalized with the radius
${\mathit{Re}}_{\omega } {r}^{2} \ll t$, where the characteristic length and velocity are respectively normalized with the radius 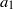 ${a}_{1} $ of the circular cylinder and the circumferential velocity
${a}_{1} $ of the circular cylinder and the circumferential velocity 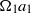 ${\Omega }_{1} {a}_{1} $. Then, the influence of the Reynolds number
${\Omega }_{1} {a}_{1} $. Then, the influence of the Reynolds number 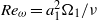 ${\mathit{Re}}_{\omega } = { a}_{1}^{2} {\Omega }_{1} / \nu $ about the two-cylinder cluster is investigated in the range
${\mathit{Re}}_{\omega } = { a}_{1}^{2} {\Omega }_{1} / \nu $ about the two-cylinder cluster is investigated in the range 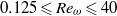 $0. 125\leqslant {\mathit{Re}}_{\omega } \leqslant 40$. The convection influence forms a pair of circulations (called self-induced closed streamlines) ahead of the cylinders to alter the symmetry of the streamline whereas the low-Reynolds-number computation (
$0. 125\leqslant {\mathit{Re}}_{\omega } \leqslant 40$. The convection influence forms a pair of circulations (called self-induced closed streamlines) ahead of the cylinders to alter the symmetry of the streamline whereas the low-Reynolds-number computation (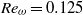 ${\mathit{Re}}_{\omega } = 0. 125$) reaches the steady regime in a proper inner domain. The self-induced closed streamline is formed at far field due to the boundary condition being zero at infinity. When the two-cylinder cluster is immersed in a uniform flow, which is equivalent to Jeffery’s solution, the streamline behaves like excellent Jeffery’s flow at
${\mathit{Re}}_{\omega } = 0. 125$) reaches the steady regime in a proper inner domain. The self-induced closed streamline is formed at far field due to the boundary condition being zero at infinity. When the two-cylinder cluster is immersed in a uniform flow, which is equivalent to Jeffery’s solution, the streamline behaves like excellent Jeffery’s flow at 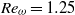 ${\mathit{Re}}_{\omega } = 1. 25$ (although the drag force is almost zero). On the other hand, the influence of the gap spacing between the cylinders is also investigated and it is shown that there are two kinds of flow regimes including Jeffery’s flow. At a proper distance from the cylinders, the self-induced far-field velocity, which is almost equivalent to Jeffery’s solution, is successfully observed in a two-cylinder arrangement.
${\mathit{Re}}_{\omega } = 1. 25$ (although the drag force is almost zero). On the other hand, the influence of the gap spacing between the cylinders is also investigated and it is shown that there are two kinds of flow regimes including Jeffery’s flow. At a proper distance from the cylinders, the self-induced far-field velocity, which is almost equivalent to Jeffery’s solution, is successfully observed in a two-cylinder arrangement.
- Type
- Papers
- Information
- Copyright
- ©2013 Cambridge University Press
Footnotes
Professor Emeritus.
References
- 5
- Cited by


