Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-26T09:14:23.690Z Has data issue: false hasContentIssue false
  • English
  • Français

Statistical structure of self-sustaining attached eddies in turbulent channel flow

Published online by Cambridge University Press:  12 February 2015

Yongyun Hwang
Yongyun Hwang*
Affiliation:
Department of Aeronautics, Imperial College London, South Kensington, London SW7 2AZ, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The linear growth of the spanwise correlation length scale with the distance from the wall in the logarithmic region of wall-bounded turbulent flows has been understood as a reflection of Townsend’s attached eddies. Based on this observation, in the present study, we perform a numerical experiment, which simulates energy-containing motions only at a given spanwise length scale in the logarithmic region, using their self-sustaining nature found recently. The self-sustaining energy-containing motions at each of the spanwise length scales are found to be self-similar with respect to the given spanwise length. Furthermore, their statistical structures are consistent with those of the attached eddies in the original theory, providing direct evidence on the existence of Townsend’s attached eddies. It is shown that a single self-sustaining attached eddy is composed of two distinct elements, one of which is a long streaky motion reaching the near-wall region, and the other is a relatively short vortical structure carrying all the velocity components. For the given spanwise length 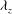${\it\lambda}_{z}$ between 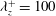${\it\lambda}_{z}^{+}=100$ and 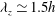${\it\lambda}_{z}\simeq 1.5h$, where 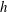$h$ is half the height of the channel, the former is found to be self-similar along 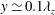$y\simeq 0.1{\it\lambda}_{z}$ and 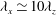${\it\lambda}_{x}\simeq 10{\it\lambda}_{z}$, while the latter is self-similar along 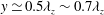$y\simeq 0.5{\it\lambda}_{z}\sim 0.7{\it\lambda}_{z}$ and 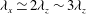${\it\lambda}_{x}\simeq 2{\it\lambda}_{z}\sim 3{\it\lambda}_{z}$ where 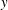$y$ is the wall-normal direction. The scaling suggests that the smallest attached eddy would be a near-wall coherent motion in the form of a streak and quasi-streamwise vortices aligned to that, whereas the largest one would be an outer motion with a very-large-scale motion (VLSM) and large-scale motions (LSMs) aligned to that. The attached eddies in between, the size of which is proportional to their distance from the wall, contribute to the logarithmic region and fill the space caused by the length scale separation. The scaling is also found to yield behaviour consistent with the emergence of 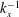$k_{x}^{-1}$ spectra in a number of previous studies. Finally, a further discussion is provided, in particular on Townsend’s inactive motion and several recent theoretical findings.

JFM classification

Turbulent Flows: Turbulence simulation Turbulent Flows: Turbulence theory Turbulent Flows: Turbulent boundary layers
Type
Papers
Information
Journal of Fluid Mechanics , Volume 767 , 25 March 2015 , pp. 254 - 289
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adrian, R. J. 2007 Hairpin vortex organization in wall turbulence. Phys. Fluids 19, 041301.Google Scholar
del Álamo, J. C. & Jiménez, J. 2003 Spectra of the very large anisotropic scales in turbulent channels. Phys. Fluids 15, L41.Google Scholar
del Álamo, J. C. & Jiménez, J. 2006 Linear energy amplification in turbulent channels. J. Fluid Mech. 559, 205–213.Google Scholar
del Álamo, J. C., Jiménez, J., Zandonade, P. & Moser, R. D. 2004 Scaling of the energy spectra of turbulent channels. J. Fluid Mech. 500, 135–144.Google Scholar
del Álamo, J. C., Jiménez, J., Zandonade, P. & Moser, R. D. 2006 Self-similar vortex clusters in the turbulent logarithmic region. J. Fluid Mech. 561, 329–358.Google Scholar
Andersson, P., Brandt, L., Bottaro, A. & Henningson, D. 2001 On the breakdown of boundary layers streaks. J. Fluid Mech. 428, 29–60.Google Scholar
Balakumar, B. J. & Adrian, R. J. 2007 Large- and very-large-scale motions in channel and boundary layer flows. Phil. Trans. R. Soc. Lond. A 365, 665–681.Google ScholarPubMed
Butler, K. M. & Farrell, B. F. 1993 Optimal perturbations and streak spacing in wall-bounded turbulent shear flow. Phys. Fluids 5, 774–777.CrossRefGoogle Scholar
Chung, D., Monty, J. P. & Ooi, A. 2014 An idealised assessment of townsend’s outer-layer similarity hypothesis for wall turbulence. J. Fluid Mech. 742, R3.Google Scholar
Cossu, C., Pujals, G. & Depardon, S. 2009 Optimal transient growth and very large scale structures in turbulent boundary layers. J. Fluid Mech. 619, 79–94.CrossRefGoogle Scholar
De Graaff, D. B. & Eaton, J. K. 2000 Reynolds-number scaling of the flat-plate turbulent boundary layer. J. Fluid Mech. 422, 319–346.Google Scholar
Dennis, D. J. C. & Nikels, T. B. 2011a Experimental measurement of large-scale three-dimensional structures in a turbulent boundary layer. Part 1. Vortex packets. J. Fluid Mech. 673, 180–217.Google Scholar
Dennis, D. J. C. & Nikels, T. B. 2011b Experimental measurement of large-scale three-dimensional structures in a turbulent boundary layer. Part 2. Long structures. J. Fluid Mech. 673, 218–244.CrossRefGoogle Scholar
Faisst, H. & Eckhardt, B. 2003 Travelling waves in pipe flow. Phys. Rev. Lett. 91, 224502.Google Scholar
Flores, O. & Jiménez, J. 2006 Effect of wall-boundary disturbances on turbulent channel flows. J. Fluid Mech. 566, 357–376.Google Scholar
Flores, O. & Jiménez, J. 2010 Hierarchy of minimal flow units in the logarithmic layer. Phys. Fluids 22, 071704.Google Scholar
Flores, O., Jiménez, J. & del Álamo, J. C. 2007 Vorticity organization in the outer layer of turbulent channels with disturbed walls. J. Fluid Mech. 591, 145–154.Google Scholar
Ganapathisubramani, B., Hutchins, N., Hambleton, W. T., Longmire, E. K. & Marusic, I. 2005 Investigation of large-scale coherence in a turbulent boundary layer using two-point correlation. J. Fluid Mech. 524, 57–80.Google Scholar
Ganapathisubramani, B., Longmire, E. K. & Marusic, I. 2003 Characteristics of vortex packets in turbulent boundary layers. J. Fluid Mech. 478, 35–46.Google Scholar
Germano, M., Piomelli, U., Moin, P. & Cabot, W. H. 1991 A dynamic subgridscale eddy viscosity model. Phys. Fluids 3, 1760.Google Scholar
Gibson, J. F., Halcrow, J. & Cvitanovic, P. 2008 Visualizing the geometry of state space in plane Couette flow. J. Fluid Mech. 611, 107–130.Google Scholar
Guala, M., Hommema, S. E. & Adrian, R. J. 2006 Large-scale and very-large-scale motions in turbulent pipe flow. J. Fluid Mech. 554, 521–541.Google Scholar
Hall, P. & Sherwin, S. J. 2010 Streamwise vortices in shear flows: harbingers of transition and the skeleton of coherent structures. J. Fluid Mech. 661, 178–205.Google Scholar
Hamilton, J. M., Kim, J. & Waleffe, F. 1995 Regeneration mechanisms of near-wall turbulence structures. J. Fluid Mech. 287, 317–348.Google Scholar
Härtel, C. & Kleiser, L. 1998 Analysis and modelling of subgrid-scale motions in near-wall turbulence. J. Fluid Mech. 356, 327–352.Google Scholar
Head, M. R. & Bandyopadhay, P. 1981 New aspects of turbulent boundary-layer structure. J. Fluid Mech. 107, 297–338.Google Scholar
Hoyas, S. & Jiménez, J. 2006 Scaling of the velocity fluctuations in turbulent channels up to $Re_{{\it\tau}}=2003$ . Phys. Fluids 18, 011702.Google Scholar
Hutchins, N., Hambleton, W. T. & Marusic, I. 2005 Inclined cross-stream stereo particle image velocimetry measurements in turbulent boundary layers. J. Fluid Mech. 541, 21–54.Google Scholar
Hutchins, N. & Marusic, I. 2007 Evidence of very long meandering features in the logarithmic region of turbulent boundary layers. J. Fluid Mech. 579, 1–28.CrossRefGoogle Scholar
Hwang, Y. 2013 Near-wall turbulent fluctuations in the absence of wide outer motions. J. Fluid Mech. 723, 264–288.Google Scholar
Hwang, Y. & Cossu, C. 2010a Amplification of coherent streaks in the turbulent Couette flow: an input–output analysis at low Reynolds number. J. Fluid Mech. 643, 333–348.Google Scholar
Hwang, Y. & Cossu, C. 2010b Linear non-normal energy amplification of harmonic and stochastic forcing in the turbulent channel flow. J. Fluid Mech. 664, 51–73.Google Scholar
Hwang, Y. & Cossu, C. 2010c Self-sustained process at large scales in turbulent channel flow. Phys. Rev. Lett. 105, 044505.Google Scholar
Hwang, Y. & Cossu, C. 2011 Self-sustained processes in the logarithmic layer of turbulent channel flows. Phys. Fluids 23, 061702.Google Scholar
Jeong, J., Benney, F., Schoppa, W. & Kim, J. 1997 Coherent structures near the wall in a turbulent channel flow. J. Fluid Mech. 332, 185–214.Google Scholar
Jiménez, J. 2013a Near-wall turbulence. Phys. Fluids 25, 101302.Google Scholar
Jiménez, J. 2013b How linear is wall-bounded turbulence. Phys. Fluids 25, 110814.Google Scholar
Jiménez, J., del Álamo, J. C. & Flores, O. 2004 The large-scale dynamics of near-wall turbulence. J. Fluid Mech. 505, 179–199.Google Scholar
Jiménez, J. & Hoyas, S. 2008 Turbulent fluctuations above the buffer layer of wall-bounded flows. J. Fluid Mech. 611, 215–236.Google Scholar
Jiménez, J., Kawahara, G., Simens, M. P., Nagata, M. & Shiba, M. 2005 Phys. Fluids 17, 015105.Google Scholar
Jiménez, J. & Moin, P. 1991 The minimal flow unit in near-wall turbulence. J. Fluid Mech. 225, 213–240.Google Scholar
Jiménez, J. & Pinelli, A. 1999 The autonomous cycle of near-wall turbulence. J. Fluid Mech. 389, 335–359.CrossRefGoogle Scholar
Kim, K. C. & Adrian, R. 1999 Very large-scale motion in the outer layer. Phys. Fluids 11 (2), 417–422.CrossRefGoogle Scholar
Kim, J. & Moin, P. 1985 Application of a fractional-step method to incompressible Navier–Stokes equations. J. Comput. Phys. 59, 308–323.Google Scholar
Kim, J., Moin, P. & Moser, R. D. 1987 Turbulence statistics in fully developed channel flow at low Reynolds number. J. Fluid Mech. 177, 133–166.Google Scholar
Kline, S. J., Reynolds, W. C., Schraub, F. A. & Runstadler, P. W. 1967 The structure of turbulent boundary layers. J. Fluid Mech. 30, 741–773.Google Scholar
Kovasznay, L. S. G., Kibens, V. & Blackwelder, R. F. 1970 Large-scale motion in the intermittent region of a turbulent boundary layer. J. Fluid Mech. 41, 283–325.Google Scholar
Kunkel, G. J. & Marusic, I. 2006 Study of the near-wall-turbulent region of the high Reynolds-number boundary layer using an atmospheric flow. J. Fluid Mech. 548, 375–402.Google Scholar
Landahl, M. T. 1990 On sublayer streaks. J. Fluid Mech. 212, 593–614.Google Scholar
Lee, J. H., Sung, H. J. & Krogstad, P. 2011 Direct numerical simulation of the turbulent boundary layer over a cube-roughened wall. J. Fluid Mech. 669, 397–431.Google Scholar
Marusic, I. & Kunkel, G. J. 2003 Streamwise turbulent intensity formulation for flat-flate boundary layers. Phys. Fluids 15 (8), 2461.Google Scholar
Marusic, I., Monty, J. P., Hultmark, M. & Smits, A. J. 2013 On the logarithmic region in wall turbulence. J. Fluid Mech. 716, R3.Google Scholar
Marusic, I. & Perry, A. E. 1995 A wall-wake model for the turbulence structure of boundary layers. Part 2. Further experimental support. J. Fluid Mech. 298, 389–407.Google Scholar
Mason, P. J. & Cullen, N. J. 1986 On the magnitude of the subgrid-scale eddy coefficient in large-eddy simulations of turbulent channel flow. J. Fluid Mech. 162, 439–462.Google Scholar
Mathis, R., Hutchins, N. & Marusic, I. 2009 Large-scale amplitude modulation of the small-scale structures in turbulent boudnary layers. J. Fluid Mech. 628, 311–337.CrossRefGoogle Scholar
Meneveau, C. & Marusic, I. 2013 Generalized logarithmic law for high-order moments in turbulent boundary layers. J. Fluid Mech. 719, R1.Google Scholar
Metzger, M. M. & Klewicki, J. C. 2001 A comparative study of near-wall turbulence in high and low Reynolds number boundary layers. Phys. Fluids 13, 692–701.Google Scholar
Millikan, C. B.1938 A critical discussion of turbulent flows in channels and circular tubes. In Proceedings of the Fifth International Congress of Applied Mechanics.Google Scholar
Mizuno, Y. & Jiménez, J. 2011 Mean velocity and length-scales in the overlap region of wall-bounded turbulent flows. Phys. Fluids 23, 085112.Google Scholar
Monty, J. P., Hutchins, N., NG, H. C. H., Marusic, I. & Chong, M. S. 2009 A comparison of turbulent pipe, channel and boundary layer flows. J. Fluid Mech. 632, 431–442.Google Scholar
Nagata, M. 1990 Three-dimensional finite-amplitude solutions in plane Couette flow: bifurcation from infinity. J. Fluid Mech. 217, 519–527.Google Scholar
Nickels, T. B., Marusic, I., Hafez, S. & Chong, M. S. 2005 Evidence of the $k-1$ law in a high Reynolds number turbulent boundary layer. Phys. Rev. Lett. 95, 074501.Google Scholar
Nickels, T. B., Marusic, I., Hafez, S. M., Hutchins, N. & Chong, M. S. 2007 Some predictions of the attached eddy model for a high Reynolds number boundary layer. Phil. Trans. R. Soc. Lond. A 365, 807–822.Google Scholar
Park, J., Hwang, Y. & Cossu, C. 2011 On the stability of large-scale streaks in the turbulent Couette and Poiseulle flows. C. R. Mèc. 339 (1), 1–5.CrossRefGoogle Scholar
Park, N., Lee, S., Lee, J. & Choi, H. 2006 A dynamic subgrid-scale eddy viscosity model with a global model coefficient. Phys. Fluids 18, 125109.CrossRefGoogle Scholar
Perry, A. E. & Chong, M. S. 1982 On the mechanism of turbulence. J. Fluid Mech. 119, 173–217.Google Scholar
Perry, A. E., Henbest, S. & Chong, M. S. 1986 A theoretical and experimental study of wall turbulence. J. Fluid Mech. 165, 163–199.Google Scholar
Perry, A. E., Li, J. D. & Marusic, I. 1991a Towards a closure scheme for turbulent boundary layers using the attached eddy hypothesis. Phil. Trans. R. Soc. Lond. A 336, 67–79.Google Scholar
Perry, A. E., Lim, K. L. & Chong, S. M. 1990 Experimental support for the attached-eddy hypothesis in zero-pressure-gradient turbulent boundary layers. J. Fluid Mech. 218, 405–438.Google Scholar
Perry, A. E. & Marusic, I. 1995 A wall-wake model for the turbulence structure of boundary layers. Part 1. Extension of the attached eddy hypothesis. J. Fluid Mech. 298, 361–388.Google Scholar
Perry, A. E., Marusic, I. & Li, J. D. 1991b Wall-turbulence closure based on classical similarity laws and the attached eddy hypothesis. Phil. Trans. R. Soc. Lond. A 336, 67–79.Google Scholar
Pirozzoli, S. 2012 On the size of the energy-containing eddies in the outer turbulent wall layer. J. Fluid Mech. 702, 521–532.Google Scholar
Pujals, G., García-Villalba, M., Cossu, C. & Depardon, S. 2009 A note on optimal transient growth in turbulent channel flows. Phys. Fluids 21, 015109.Google Scholar
Schmid, P. J. & Henningson, D. S. 2001 Stability and Transition in Shear Flows. Springer.Google Scholar
Schoppa, W. & Hussain, F. 2002 Coherent structure generation in near-wall turbulence. J. Fluid Mech. 453, 57–108.Google Scholar
Sharma, A. & Mckeon, B. J. 2013 On coherent structure in wall turbulence. J. Fluid Mech. 728, 196–238.Google Scholar
Smith, J. R. & Metzler, S. P. 1983 The characteristics of low-speed streaks in the near-wall region of a turbulent boundary layer. J. Fluid Mech. 129, 27–54.Google Scholar
Talluru, K. M., Baidya, R., Hutchins, N. & Marusic, I. 2014 Amplitude modulation of all three velocity components in turbulent boundary layers. J. Fluid Mech. 746, R1.Google Scholar
Tomkins, C. D. & Adrian, R. J. 2003 Spanwise structure and scale growth in turbulent boundary layers. J. Fluid Mech. 490, 37–74.Google Scholar
Tomkins, C. D. & Adrian, R. J. 2005 Energetic spanwise modes in the logarithmic layer of a turbulent boundary layer. J. Fluid Mech. 545, 141–162.Google Scholar
Townsend, A. A. 1961 Equilibrium layers and wall turbulence. J. Fluid Mech. 11 (1), 97–120.Google Scholar
Townsend, A. A. 1976 The Structure of Turbulent Shear Flow. Cambridge University Press.Google Scholar
Tuerke, F. & Jiménez, J. 2013 Simulations of turbulent channels with prescribed velocity profiles. J. Fluid Mech. 723, 587–603.Google Scholar
Waleffe, F. 1997 On a self-sustaining process in shear flows. Phys. Fluids 9, 883–900.Google Scholar
Waleffe, F. 1998 Three-dimensional coherent states in plane shear flows. Phys. Rev. Lett. 81, 4140–4143.Google Scholar
Waleffe, F. 2001 Exact coherent structures in channel flow. J. Fluid Mech. 435, 93–102.Google Scholar
Waleffe, F. 2003 Homotopy of exact coherent structures in plane shear flows. Phys. Fluids 15, 1517–1534.Google Scholar
Wedin, H. & Kerswell, R. R. 2004 Exact coherent structures in pipe flow: travelling wave solutions. J. Fluid Mech. 508, 333–371.Google Scholar
Willis, A. P., Hwang, Y. & Cossu, C. 2010 Optimally amplified large-scale streaks and drag reduction in the turbulent pipe flow. Phys. Rev. E 82, 036321.Google Scholar
Zang, T. A. 1991 Numerical simulation of the dynamics of turbulent boundary layers: perspectives of a transition simulator. Phil. Trans. R. Soc. Lond. A 336, 95–102.Google Scholar