Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-23T14:56:10.542Z Has data issue: false hasContentIssue false
  • English
  • Français

The stably stratified Taylor–Couette flow is always unstable except for solid-body rotation

Published online by Cambridge University Press:  14 May 2013

Junho Park  and
Paul Billant
Junho Park*
Affiliation:
LadHyX, CNRS, Ecole Polytechnique, F-91128 Palaiseau CEDEX, France
Paul Billant
Affiliation:
LadHyX, CNRS, Ecole Polytechnique, F-91128 Palaiseau CEDEX, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

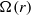The stability of the flow between two concentric cylinders is studied numerically and analytically when the fluid is stably stratified. We show that such flow is unstable when the angular velocity $\Omega (r)$ increases along the radial direction, a regime never explored before. The instability is highly non-axisymmetric and involves the resonance of two families of inertia–gravity waves like for the strato-rotational instability. The growth rate is maximum when only the outer cylinder is rotating and goes to zero when 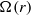$\Omega (r)$ is constant. The sufficient condition for linear, inviscid instability derived previously, 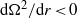$\mathrm{d} {\Omega }^{2} / \mathrm{d} r\lt 0$, is therefore extended to 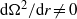$\mathrm{d} {\Omega }^{2} / \mathrm{d} r\not = 0$, meaning that only the regime of solid-body rotation is stable in stratified fluids. A Wentzel–Kramers–Brillouin–Jeffreys (WKBJ) analysis in the inviscid limit, confirmed by the numerical results, shows that the instability occurs only when the Froude number is below a critical value and only for a particular band of azimuthal wavenumbers. It is also demonstrated that the instability originates from a reversal of the radial group velocity of the waves, or equivalently from a wave over-reflection phenomenon. The instability persists in the presence of viscous effects.

JFM classification

Instability: Instability Geophysical and Geological Flows: Stratified flows Vortex Flows: Vortex Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 725 , 25 June 2013 , pp. 262 - 280
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Andereck, C. D., Liu, S. S. & Swinney, H. L. 1986 Flow regimes in a circular Couette system with independently rotating cylinders. J. Fluid Mech. 164, 155–183.CrossRefGoogle Scholar
Antkowiak, A. & Brancher, P. 2004 Transient energy growth for the Lamb–Oseen vortex. Phys. Fluids 16, L1–L4.CrossRefGoogle Scholar
Bender, C. M. & Orszag, S. A. 1978 Advanced Mathematical Methods for Scientists and Engineers. McGraw-Hill.Google Scholar
Billant, P. & Gallaire, F. 2005 Generalized Rayleigh criterion for non-axisymmetric centrifugal instabilities. J. Fluid Mech. 542, 365–379.Google Scholar
Billant, P. & Le Dizès, S. 2009 Waves on a columnar vortex in a strongly stratified fluid. Phys. Fluids 21, 106602.CrossRefGoogle Scholar
Boubnov, B. M., Gledzer, E. B. & Hopfinger, E. J. 1995 Stratified circular Couette flow: instability and flow regimes. J. Fluid Mech. 292, 333–358.Google Scholar
Caton, F., Janiaud, B. & Hopfinger, E. J. 2000 Stability and bifurcations in stratified Taylor–Couette flow. J. Fluid Mech. 419, 93–124.Google Scholar
Dubrulle, B., Dauchot, O., Daviaud, F., Longaretti, P.-Y., Richard, D. & Zahn, J.-P. 2005a Stability and turbulent transport in Taylor–Couette flow from analysis of experimental data. Phys. Fluids 17, 095103.Google Scholar
Dubrulle, B., Marié, L., Normand, C., Richard, D., Hersant, F. & Zahn, J. P. 2005b An hydrodynamic shear instability in stratified disks. Astron. Astrophys. 429, 1–13.Google Scholar
Fabre, D. & Jacquin, L. 2004 Viscous instabilities in trailing vortices at large swirl numbers. J. Fluid. Mech. 500, 239–262.CrossRefGoogle Scholar
Hua, B. L., Le Gentil, S. & Orlandi, P. 1997a First transitions in circular Couette flow with axial stratification. Phys. Fluids 9, 365–375.Google Scholar
Hua, B. L., Moore, D. W. & Le Gentil, S. 1997b Inertial nonlinear equilibration of equatorial flows. J. Fluid Mech. 331, 345–371.CrossRefGoogle Scholar
Le Bars, M. & Le Gal, P. 2007 Experimental analysis of the stratorotational instability in a cylindrical Couette flow. Phys. Rev. Lett. 99, 064502.Google Scholar
Le Dizès, S. & Billant, P. 2009 Radiative instability in stratified vortices. Phys. Fluids 21, 096602.Google Scholar
Le Dizès, S. & Lacaze, L. 2005 An asymptotic description of vortex Kelvin modes. J. Fluid Mech. 542, 69–96.Google Scholar
Le Dizès, S. & Riedinger, X. 2010 The strato-rotational instability of Taylor–Couette and Keplerian flows. J. Fluid Mech. 660, 147–161.Google Scholar
Lindzen, R. S., Farrell, B. & Tung, K.-K. 1980 The concept of wave overreflection and its application to baroclinic instability. J. Atmos. Sci. 37, 44–63.2.0.CO;2>CrossRefGoogle Scholar
Ménesguen, C., Hua, B. L., Papenberg, C., Klaeschen, D., Géli, L. & Hobbs, R. 2009 Effect of bandwidth on seismic imaging of rotating stratified turbulence surrounding an anticyclonic eddy from field data and numerical simulations. Geophys. Res. Lett. 36, L00D05.Google Scholar
Molemaker, M. J., McWilliams, J. C. & Yavneh, I. 2001 Instability and equilibration of centrifugally stable stratified Taylor–Couette flow. Phys. Rev. Lett. 86, 5270–5273.Google Scholar
Ooyama, K. 1966 On the stability of the baroclinic circular vortex: a sufficient criterion for instability. J. Atmos. Sci. 23, 43–53.Google Scholar
Park, J. 2012 Waves and instabilities on vortices in stratified and rotating fluids. PhD thesis, Ecole Polytechnique.Google Scholar
Park, J. & Billant, P. 2012 Radiative instability of an anticyclonic vortex in a stratified rotating fluid. J. Fluid Mech. 707, 381–392.Google Scholar
Park, J. & Billant, P. 2013 Instabilities and waves on a columnar vortex in a strongly-stratified and rotating fluid. Phys. Fluids (submitted).CrossRefGoogle Scholar
Riedinger, X., Le Dizès, S. & Meunier, P. 2011 Radiative instability of the flow around a rotating cylinder in a stratified fluid. J. Fluid Mech. 672, 130–146.Google Scholar
Riedinger, X., Meunier, P. & Le Dizès, S. 2010 Instability of a vertical columnar vortex in a stratified fluid. Exp. Fluids 49, 673–681.CrossRefGoogle Scholar
Schecter, D. A. & Montgomery, M. T. 2004 Damping and pumping of a vortex Rossby wave in a monotonic cyclone: critical layer stirring versus inertia–buoyancy wave emission. Phys. Fluids 26 (5), 1334–1348.Google Scholar
Shalybkov, D. & Rüdiger, G. 2005 Stability of density-stratified viscous Taylor–Couette flows. Astron. Astrophys. 438, 411–417.Google Scholar
Takehiro, S. & Hayashi, Y. 1992 Over-reflection and shear instability in a shallow-water model. J. Fluid Mech. 236, 259–279.Google Scholar
Vanneste, J. & Yavneh, I. 2007 Unbalanced instabilities of rapidly rotating stratified shear flows. J. Fluid Mech. 584, 373–396.Google Scholar
Withjack, E. M. & Chen, C. F. 1974 An experimental study of Couette instability of stratified fluids. J. Fluid Mech. 66, 725–737.Google Scholar
Yavneh, I., McWilliams, J. C. & Molemaker, M. J. 2001 Non-axisymmetric instability of centrifugally stable staratified Taylor–Couette flow. J. Fluid Mech. 448, 1–21.Google Scholar