Hostname: page-component-745bb68f8f-s22k5 Total loading time: 0 Render date: 2025-01-25T06:09:35.113Z Has data issue: false hasContentIssue false
  • English
  • Français

Stable–streamlined and helical cavities following the impact of Leidenfrost spheres

Published online by Cambridge University Press:  23 June 2017

M. M. Mansoor Open the ORCID record for M. M. Mansoor [Opens in a new window] ,
I. U. Vakarelski ,
J. O. Marston ,
T. T. Truscott Open the ORCID record for T. T. Truscott [Opens in a new window]  and
S. T. Thoroddsen
M. M. Mansoor*
Affiliation:
Division of Physical Sciences and Engineering, King Abdullah University of Science and Technology, Thuwal 23955-6900, Saudi Arabia
I. U. Vakarelski
Affiliation:
Division of Physical Sciences and Engineering, King Abdullah University of Science and Technology, Thuwal 23955-6900, Saudi Arabia
J. O. Marston
Affiliation:
Department of Chemical Engineering, Texas Tech University, Lubbock, TX 79409-3121, USA
T. T. Truscott
Affiliation:
Department of Mechanical and Aerospace Engineering, Utah State University, Logan, UT 84322-4130, USA
S. T. Thoroddsen
Affiliation:
Division of Physical Sciences and Engineering, King Abdullah University of Science and Technology, Thuwal 23955-6900, Saudi Arabia
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We report results from an experimental study on the formation of stable–streamlined and helical cavity wakes following the free-surface impact of Leidenfrost spheres. Similar to the observations of Mansoor et al. (J. Fluid Mech., vol. 743, 2014, pp. 295–326), we show that acoustic ripples form along the interface of elongated cavities entrained in the presence of wall effects as soon as the primary cavity pinch-off takes place. The crests of these ripples can act as favourable points for closure, producing multiple acoustic pinch-offs, which are found to occur in an acoustic pinch-off cascade. We show that these ripples pacify with time in the absence of physical contact between the sphere and the liquid, leading to extremely smooth cavity wake profiles. More importantly, the downward-facing jet at the apex of the cavity is continually suppressed due to a skin-friction drag effect at the colliding cavity-wall junction, which ultimately produces a stable–streamlined cavity wake. This streamlined configuration is found to experience drag coefficients an order of a magnitude lower than those acting on room-temperature spheres. 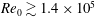A striking observation is the formation of helical cavities which occur for impact Reynolds numbers $Re_{0}\gtrsim 1.4\times 10^{5}$ and are characterized by multiple interfacial ridges, stemming from and rotating synchronously about an evident contact line around the sphere equator. The contact line is shown to result from the degeneration of Kelvin–Helmholtz billows into turbulence which are observed forming along the liquid–vapour interface around the bottom hemisphere of the sphere. Using sphere trajectory measurements, we show that this helical cavity wake configuration has 40 %–55 % smaller force coefficients than those obtained in the formation of stable cavity wakes.

JFM classification

Drops and Bubbles: Cavitation Interfacial Flows (free surface): Contact lines Flow Control: Drag reduction
Type
Papers
Information
Journal of Fluid Mechanics , Volume 823 , 25 July 2017 , pp. 716 - 754
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Achenbach, E. 1972 Experiments on the flow past spheres at very high Reynolds numbers. J. Fluid Mech. 54, 565–575.Google Scholar
Achenbach, E. 1974 Vortex shedding from spheres. J. Fluid Mech. 62, 209–221.Google Scholar
Affeld, K., Schichl, K. & Ziemann, A. 1993 Assessment of rowing efficiency. Int. J. Sports. Med. 14 (1), 39–41.Google Scholar
Aristoff, J. M. & Bush, J. W. M. 2009 Water entry of small hydrophobic spheres. J. Fluid Mech. 619, 45–78.Google Scholar
Aristoff, J. M., Truscott, T., Techet, A. H. & Bush, J. W. M. 2010 The water entry of decelerating spheres. Phys. Fluids 22, 032102.Google Scholar
Baumeister, K. J. & Simon, F. F. 1973 Leidenfrost temperature – its correlation for liquid metals, cryogens, hydrocarbons, and water. Trans. ASME J. Heat Transfer 95 (2), 166–173.Google Scholar
Berklite, R. B.1972 Added mass of submerged objects of arbitrary shape. Ms thesis, Naval Postgraduate School, Monterey, CL.Google Scholar
Bodily, K. G., Carlson, S. J. & Truscott, T. T. 2014 The water entry of slender axisymmetric bodies. Phys. Fluids A 26, 072108.Google Scholar
de Boor, C. 1978 A Practical Guide to Splines. Springer.Google Scholar
Brennen, C. 1970 Cavity surface wave patterns and general appearance. J. Fluid Mech. 44 (1), 33–49.Google Scholar
Burley, R. 1992 Air entrainment and the limits of coatability. JOCCA 75 (5), 192–202.Google Scholar
Chen, W., Xia, D., Liu, J. & Wang, R. 2010 Influence of geometric parameters on the flow drag of a streamlined body of revolution. In 2010 4th International Conference on Bioinformatics and Biomedical Engineering, pp. 1–4. IEEE.Google Scholar
Chomaz, J. M., Bonneton, P. & Hopfinger, E. J. 1993 The structure of the near wake of a sphere moving horizontally in a stratified fluid. J. Fluid Mech. 254, 1–21.Google Scholar
Clanet, C. 2007 Waterbells and liquid sheets. Annu. Rev. Fluid Mech. 39, 469–496.Google Scholar
Cometta, C.1957 An investigation of the unsteady flow pattern in the wake of cylinders and spheres using a hot wire probe. Tech. Rep. WT-21. Div. Engng, Brown University.Google Scholar
Constantinescu, G. & Squires, K. 2004 Numerical investigations of flow over a sphere in the subcritical and supercritical regimes. Phys. Fluids 16, 1449–1466.Google Scholar
Corcos, G. M. & Sherman, F. S. 1976 Vorticity concentration and the dynamics of unstable free shear layers. J. Fluid Mech. 73, 241–264.Google Scholar
Dong, R. G.1978 Effective mass and damping of submerged structures. California Univ., Livermore, Lawrence Livermore Lab.Google Scholar
Duclaux, V., Caille, F., Duez, C., Ybert, C., Bocquet, L. & Clanet, C. 2007 Dynamics of transient cavities. J. Fluid Mech. 591, 1–19.Google Scholar
Duez, C., Ybert, C., Clanet, C. & Bocquet, L. 2007 Making a splash with water repellency. Nat. Phys. 3, 180–183.Google Scholar
Enríquez, O. R., Peters, I. R., Gekle, S., Schmidt, L. E., Lohse, D. & Van der Meer, D. 2012 Collapse and pinch-off of a non-axisymmetric impact-created air cavity in water. J. Fluid Mech. 701, 40–58.Google Scholar
Epps, B. P., Truscott, T. T. & Techet, A. H. 2010 Evaluating derivatives of experimental data using smoothing splines. In Proceedings of Mathematical Methods in Engineering International Symposium. MMEI, Lisbon, Portugal.Google Scholar
Fernando, H. J. S. 1991 Turbulent mixing in stratified fluids. Annu. Rev. Fluid Mech. 23, 455–493.Google Scholar
Gekle, S., Gordillo, J. M., Van der Meer, D. & Lohse, D. 2009 High-speed jet formation after solid object impact. Phys. Rev. Lett. 102, 034502.Google Scholar
Gekle, S., Peters, I. R., Gordillo, J. M., Van der Meer, D. & Lohse, D 2010 Supersonic air flow due to solid–liquid impact. Phys. Rev. Lett. 104, 024501.Google Scholar
Gekle, S., Van der Bos, A., Bergmann, R., Van der Meer, D. & Lohse, D. 2008 Noncontinuous Froude number scaling for the closure depth of a cylindrical cavity. Phys. Rev. Lett. 100, 084502.Google Scholar
Gilbarg, D. & Anderson, R. 1948 Influence of atmospheric pressure on the phenomena accompanying the entry of spheres into water. J. Appl. Phys. 19, 127–139.Google Scholar
Goldstein, S. 1931 On the stability of superposed streams of fluids of different densities. Proc. R. Soc. Lond. A 132, 524–548.Google Scholar
Grumstrup, T., Keller, J. B. & Belmonte, A. 2007 Cavity ripples observed during the impact of solid objects into liquids. Phys. Rev. Lett. 99, 114502.Google Scholar
Hall, R. S., Board, S. J., Clare, A. J., Duffy, R. B., Playle, T. S. & Poole, D. H. 1969 Inverse Leidenfrost phenomenon. Nature 224, 266–267.Google Scholar
Hazel, P. 1972 Numerical studies of the stability of inviscid stratified shear flows. J. Fluid Mech. 51, 39–61.Google Scholar
Hedrick, T. L. 2008 Software techniques for two- and three-dimensional kinematic measurements of biological and biomimetic systems. Bioinspir. Biomim. 3, 034001.Google Scholar
Howard, L. N. 1961 Note on a paper of John W. Miles. J. Fluid Mech. 10, 509–512.Google Scholar
Johnson, T. A. & Patel, V. C. 1999 Flow past a sphere up to a Reynolds number of 300. J. Fluid Mech. 378, 19–70.Google Scholar
von Kármán, T.1929 The impact on seaplane floats during landing. Tech. Note 321. Natl. Advis. Comm. Aeronaut. Washington, DC.Google Scholar
Kim, H. J. & Durbin, P. A. 1988 Observations of the frequencies in a sphere wake and of drag increase by acoustic excitation. Phys. Fluids 31, 3260–3265.Google Scholar
Kruse, C., Anderson, T., Wilson, C., Zulke, C., Alexander, D., Gogos, G. & Ndao, S. 2013 Extraordinary shifts of the Leidenfrost temperature from multiscale micro/nanostructured surfaces. Langmuir 29, 9798–9806.Google Scholar
Lee, M., Longoria, R. G. & Wilson, D. E. 1997 Cavity dynamics in high-speed water entry. Phys. Fluids 9, 540–550.Google Scholar
Lee, T. S. & Low, H. T. 1990 Water entrance characteristics of a 60° truncated ogive nose projectile. J. Inst. Eng. Singapore 30, 49–55.Google Scholar
Leidenfrost, J. G. 1966 On the fixation of water in diverse fire. Intl J. Heat Mass Transfer 9, 1153–1166; (translated from De Aquae Communis Nonnullis Qualitatibus Tractatus (1756)).Google Scholar
Li, L., Li, H. & Chen, T. 2008 Experimental investigation on the moving characteristics of molten metal droplets impacting coolant. Exp. Therm. Fluid Sci. 32 (4), 962–972.Google Scholar
Mallock, A. 1918 Sounds produced by drops falling on water. Proc. R. Soc. Lond. A 95, 138–143.Google Scholar
Magarvey, R. H. & Bishop, R. L. 1961 Wakes in liquid–liquid systems. Phys. Fluids 4, 800–805.Google Scholar
Mansoor, M. M., Marston, J. O., Vakarelski, I. U. & Thoroddsen, S. T. 2014 Water entry without surface seal: extended cavity formation. J. Fluid Mech. 743, 295–326.Google Scholar
Marston, J. O., Mansoor, M. M., Truscott, T. T. & Thoroddsen, S. T. 2015 Buckling instability of crown sealing. Phys. Fluids 27, 091112.Google Scholar
Marston, J. O., Truscott, T. T., Speirs, N. B., Mansoor, M. M. & Thoroddsen, S. T. 2016 Crown sealing and buckling instability during water entry of spheres. J. Fluid Mech. 794, 506–529.Google Scholar
Marston, J. O., Vakarelski, I. U. & Thoroddsen, S. T. 2012 Cavity formation by the impact of Leidenfrost spheres. J. Fluid Mech. 699, 465–488.Google Scholar
May, A. 1951 Effect of surface condition of a sphere on its water-entry cavity. J. Appl. Phys. 22, 1219–1222.Google Scholar
May, A. 1952 Vertical entry of missiles into water. J. Appl. Phys. 22, 1362–1372.Google Scholar
May, A.1975 Water entry and the cavity-running behavior of missiles. SEAHAC Tech. Rep. 75-2. Nav. Surf. Weapons Cent., White Oak Lab., Silver Spring, Maryland.Google Scholar
Miles, J. W. 1961 On the stability of heterogeneous shear flows. J. Fluid Mech. 10, 496–508.Google Scholar
Moghisi, M. & Squire, P. T. 1981 An experimental investigation of the initial force of impact on a sphere striking a liquid surface. J. Fluid Mech. 108, 133–146.Google Scholar
Möller, W. 1938 Experimentelle Untersuchung zur Hydromechanik der Kugel. Phys. Z. 39, 57–80.Google Scholar
Nakamura, I. 1976 Steady wake behind a sphere. Phys. Fluids 19, 5–8.Google Scholar
Peltier, W. R. & Caulfield, C. P. 2003 Mixing efficiency in stratified shear flows. Annu. Rev. Fluid Mech. 35, 135–167.Google Scholar
Quéré, D. 2013 Leidenfrost dynamics. Annu. Rev. Fluid Mech. 45, 197–215.Google Scholar
Ramsauer, C. & Dobke, G. 1927 Die Bewegungserscheinungen des Wassers beim Durchgang schnell bewegter Kugeln. Ann. Phys. Lpz. 389, 697–720.Google Scholar
Richardson, E. G. 1948 The impact of a solid on a liquid surface. Proc. Phys. Soc. 61, 352–367.Google Scholar
Rodríguez, I., Borell, R., Lehmkuhl, O., Perez Segarra, C. D. & Oliva, A. 2011 Direct numerical simulation of the flow over a sphere at Re = 3700. J. Fluid Mech. 679, 263–287.Google Scholar
Rodríguez, I., Lehmkuhl, O., Borrell, R. & Oliva, A. 2013 Flow dynamics in the turbulent wake of a sphere at sub-critical Reynolds numbers. Comput. Fluids 80, 233–243.Google Scholar
Sakamoto, H. & Haniu, H. 1990 A study on vortex shedding from spheres in a uniform flow. Trans. ASME J. Fluids Engng 112, 386–392.Google Scholar
Sarpkaya, T.1976 Vortex shedding and resistance in harmonic flow about smooth and rough circular cylinders at high Reynolds numbers. Ms thesis, Naval Postgraduate School, Monterey, CL.Google Scholar
Strang, E. J. & Fernando, H. J. 2001 Entrainment and mixing in stratified shear flows. J. Fluid Mech. 428, 349–386.Google Scholar
Takata, Y., Hidaka, S., Cao, J. M., Nakamura, T., Yamamoto, H., Masuda, M. & Ito, T. 2005 Effect of surface wettability on boiling and evaporation. Energy 30 (2), 209–220.Google Scholar
Tan, B. C.-W., Vlaskamp, J. H. A., Denissenko, P. & Thomas, P. J. 2016 Cavity formation in the wake of falling spheres submerging into a stratified two-layer system of immiscible liquids. J. Fluid Mech. 790, 33–56.Google Scholar
Taneda, S. 1956 Experimental investigation of the wake behind a sphere at low Reynolds numbers. J. Phys. Soc. Japan 11, 1104.Google Scholar
Taneda, S. 1978 Visual observations of the flow past a sphere at Reynolds numbers between 104 and 106 . J. Fluid Mech. 85, 187–192.Google Scholar
Taylor, G. I. 1931 Effect of variation in density on the stability of superposed streams. Proc. R. Soc. Lond. A 132, 499–523.Google Scholar
Thoroddsen, S. T., Etoh, T. G., Takehara, K. & Takano, Y. 2004 Impact jetting by a solid sphere. J. Fluid Mech. 499, 139–148.Google Scholar
Tomboulidesn, A., Orszag, S. A. & Karniadakis, G. E.1993 Impact jetting by a solid sphere. AIAA Paper 93-546.Google Scholar
Tran, T., Staat, H. J. J., Prosperetti, A., Sun, C. & Lohse, D. 2012 Drop impact on superheated surfaces. Phys. Rev. Lett. 108 (3), 036101.Google Scholar
Truscott, T. T., Epps, B. P. & Belden, J. 2014 Water entry of projectiles. Annu. Rev. Fluid Mech. 46, 355–378.Google Scholar
Truscott, T. T., Epps, B. P. & Techet, A. H. 2012 Unsteady forces on spheres during free-surface water entry. J. Fluid Mech. 704, 173–210.Google Scholar
Truscott, T. T. & Techet, A. H. 2009 Water entry of spinning spheres. J. Fluid Mech. 625, 135–165.Google Scholar
Vakarelski, I. U., Berry, J. D., Chan, D. Y. C. & Thoroddsen, S. T. 2016 Leidenfrost vapor layers reduce drag without the crisis in high viscosity liquids. Phys. Rev. Lett. 117, 114503.Google Scholar
Vakarelski, I. U., Chan, D. Y. C. & Thoroddsen, S. T. 2014 Leidenfrost vapour layer moderation of the drag crisis and trajectories of superhydrophobic and hydrophilic spheres falling in water. Soft Matt. 10, 5662–5668.Google Scholar
Vakarelski, I. U., Marston, J. O., Chan, D. Y. C. & Thoroddsen, S. T. 2011 Drag reduction by Leidenfrost vapor layers. Phys. Rev. Lett. 106, 214501.Google Scholar
Vakarelski, I. U., Patankar, N. A., Marston, J. O., Chan, D. Y. C. & Thoroddsen, S. T. 2012 Stabilization of Leidenfrost vapour layer by textured superhydrophobic surfaces. Nature 489, 274–277.Google Scholar
Wagner, H. 1932 Phenomena associated with impacts and sliding on liquid surfaces. Z. Angew. Math. Mech. 12, 193–235.Google Scholar
Worthington, A. M. 1908 A Study of Splashes. Longmans, Green.Google Scholar
Worthington, A. M. & Cole, R. S. 1897 Impact with a liquid surface, studied by the aid of instantaneous photography. Phil. Trans. R. Soc. Lond. A 189, 137–148.Google Scholar
Worthington, A. M. & Cole, R. S. 1900 Impact with a liquid surface, studied by the aid of instantaneous photography: paper 2. Phil. Trans. R. Soc. Lond. A 194, 175–199.Google Scholar
Wilson, H. B., Turcotte, L. H & Halpern, D. 2003 Advanced Mathematics and Mechanics Applications using MATLAB, 3rd edn. CRC Press.Google Scholar
Xuequan, E. & Hopfinger, E. J. 1986 On mixing across an interface in stably stratified fluid. J. Fluid Mech. 166, 227–244.Google Scholar
Yun, G., Kim, D. & Choi, H. 2006 Vortical structures behind a sphere at subcritical Reynolds numbers. Phys. Fluids 18, 015102.Google Scholar
Zhao, R., Faltinsen, O. & Choi, H. 1993 Water entry of two-dimensional bodies. J. Fluid Mech. 246, 593–612.Google Scholar

Mansoor et al. supplementay movie

Video of the (a) unstable and (b) stable-streamlined cavity wake formation shown in figure 1.

Download Mansoor et al. supplementay movie(Video)
Video 6.1 MB

Mansoor et al. supplementay movie

The stable-streamlined cavity wake observed in the depth range b of figure 3.

Download Mansoor et al. supplementay movie(Video)
Video 2.1 MB

Mansoor et al. supplementay movie

Video of the helical cavity wake shown in figure 8.

Download Mansoor et al. supplementay movie(Video)
Video 2.5 MB