Article contents
Stability of two-dimensional collapsible-channel flow at high Reynolds number
Published online by Cambridge University Press: 16 February 2012
Abstract
We study the linear stability of two-dimensional high-Reynolds-number flow in a rigid parallel-sided channel, of which part of one wall has been replaced by a flexible membrane under longitudinal tension 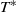 . Far upstream the flow is parallel Poiseuille flow at Reynolds number
. Far upstream the flow is parallel Poiseuille flow at Reynolds number 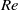 ; the width of the channel is
; the width of the channel is  and the length of the membrane is
and the length of the membrane is 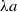 , where
, where 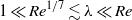 . Steady flow was studied using interactive boundary-layer theory by Guneratne & Pedley (J. Fluid Mech., vol. 569, 2006, pp. 151–184) for various values of the pressure difference
. Steady flow was studied using interactive boundary-layer theory by Guneratne & Pedley (J. Fluid Mech., vol. 569, 2006, pp. 151–184) for various values of the pressure difference 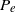 across the membrane at its upstream end. Here unsteady interactive boundary-layer theory is used to investigate the stability of the trivial steady solution for
across the membrane at its upstream end. Here unsteady interactive boundary-layer theory is used to investigate the stability of the trivial steady solution for 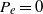 . An unexpected finding is that the flow is always unstable, with a growth rate that increases with
. An unexpected finding is that the flow is always unstable, with a growth rate that increases with 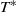 . In other words, the stability problem is ill-posed. However, when the pressure difference is held fixed (
. In other words, the stability problem is ill-posed. However, when the pressure difference is held fixed (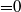 ) at the downstream end of the membrane, or a little further downstream, the problem is well-posed and all solutions are stable. The physical mechanisms underlying these findings are explored using a simple inviscid model; the crucial factor in the fluid dynamics is the vorticity gradient across the incoming Poiseuille flow.
) at the downstream end of the membrane, or a little further downstream, the problem is well-posed and all solutions are stable. The physical mechanisms underlying these findings are explored using a simple inviscid model; the crucial factor in the fluid dynamics is the vorticity gradient across the incoming Poiseuille flow.
JFM classification
- Type
- Papers
- Information
- Journal of Fluid Mechanics , Volume 705: Special issue dedicated to Professor T. J. Pedley on his 70th birthday , 25 August 2012 , pp. 371 - 386
- Copyright
- Copyright © Cambridge University Press 2012
References
- 12
- Cited by


