Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Almarcha, C.
Trevelyan, P. M. J.
Grosfils, P.
and
De Wit, A.
2013.
Thermal effects on the diffusive layer convection instability of an exothermic acid-base reaction front.
Physical Review E,
Vol. 88,
Issue. 3,
Hejazi, S. H.
and
Azaiez, J.
2013.
Nonlinear simulation of transverse flow interactions with chemically driven convective mixing in porous media.
Water Resources Research,
Vol. 49,
Issue. 8,
p.
4607.
Lemaigre, L.
Budroni, M. A.
Riolfo, L. A.
Grosfils, P.
and
De Wit, A.
2013.
Asymmetric Rayleigh-Taylor and double-diffusive fingers in reactive systems.
Physics of Fluids,
Vol. 25,
Issue. 1,
Kim, Min Chan
2014.
Effect of the irreversible A+B →C reaction on the onset and the growth of the buoyancy-driven instability in a porous medium.
Chemical Engineering Science,
Vol. 112,
Issue. ,
p.
56.
Alhumade, H.
and
Azaiez, J.
2015.
Numerical Simulations of Gravity Driven Reversible Reactive Flows in Homogeneous Porous Media.
Mathematical Problems in Engineering,
Vol. 2015,
Issue. ,
p.
1.
Trevelyan, P. M. J.
Almarcha, C.
and
De Wit, A.
2015.
Buoyancy-driven instabilities around miscibleA+B→Creaction fronts: A general classification.
Physical Review E,
Vol. 91,
Issue. 2,
De Wit, A.
2016.
Chemo-hydrodynamic patterns in porous media.
Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences,
Vol. 374,
Issue. 2078,
p.
20150419.
Bratsun, Dmitry
Mizev, Alexey
Mosheva, Elena
and
Kostarev, Konstantin
2017.
Shock-wave-like structures induced by an exothermic neutralization reaction in miscible fluids.
Physical Review E,
Vol. 96,
Issue. 5,
Sabet, Nasser
Hassanzadeh, Hassan
and
Abedi, Jalal
2017.
Control of viscous fingering by nanoparticles.
Physical Review E,
Vol. 96,
Issue. 6,
Bratsun, Dmitry
2019.
Spatial analog of the two-frequency torus breakup in a nonlinear system of reactive miscible fluids.
Physical Review E,
Vol. 100,
Issue. 3,
Kim, Min Chan
2019.
Effect of the irreversible
A+B→C
reaction on the onset and the growth of the buoyancy-driven instability in a porous medium: Asymptotic, linear, and nonlinear stability analyses.
Physical Review Fluids,
Vol. 4,
Issue. 7,
De Wit, A.
2020.
Chemo-Hydrodynamic Patterns and Instabilities.
Annual Review of Fluid Mechanics,
Vol. 52,
Issue. 1,
p.
531.
Sloman, Benjamin M.
Please, Colin P.
and
Van Gorder, Robert A.
2020.
Melting and dripping of a heated material with temperature-dependent viscosity in a thin vertical tube.
Journal of Fluid Mechanics,
Vol. 905,
Issue. ,
Michel‐Meyer, Itamar
Shavit, Uri
Tsinober, Avihai
and
Rosenzweig, Ravid
2020.
The Role of Water Flow and Dispersive Fluxes in the Dissolution of CO2 in Deep Saline Aquifers.
Water Resources Research,
Vol. 56,
Issue. 11,
Bratsun, D. A.
Mizev, A. I.
Mosheva, E. A.
and
Siraev, R. R.
2020.
Effect of channel geometry on a density wave induced by gravity and chemoconvection in miscible reacting fluids.
AIP Advances,
Vol. 10,
Issue. 12,
Mizev, A.I.
Mosheva, E.A.
and
Bratsun, D.A.
2021.
Extended classification of the buoyancy-driven flows induced by a neutralization reaction in miscible fluids. Part 1. Experimental study.
Journal of Fluid Mechanics,
Vol. 916,
Issue. ,
Bratsun, D.A.
Mizev, A.I.
and
Mosheva, E.A.
2021.
Extended classification of the buoyancy-driven flows induced by a neutralization reaction in miscible fluids. Part 2. Theoretical study.
Journal of Fluid Mechanics,
Vol. 916,
Issue. ,
Van Gorder, Robert A.
Kamilova, Alissa
Birkeland, Rolf G.
and
Krause, Andrew L.
2021.
Locating the Baking Isotherm in a Søderberg Electrode: Analysis of a Moving Thermistor Model.
SIAM Journal on Applied Mathematics,
Vol. 81,
Issue. 4,
p.
1691.
Tsypkin, G. G.
2022.
Investigation of the transition to instability of the water boiling front during injection into a geothermal reservoir.
Theoretical and Mathematical Physics,
Vol. 211,
Issue. 2,
p.
735.
Maharana, Surya Narayan
Sahu, Kirti Chandra
and
Mishra, Manoranjan
2023.
Stability of a layered reactive channel flow.
Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences,
Vol. 479,
Issue. 2271,
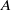 on top of another solution of reactant
on top of another solution of reactant 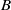 is analysed. A chemical product
is analysed. A chemical product 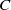 is generated at the interface as a result of a bimolecular chemical reaction
is generated at the interface as a result of a bimolecular chemical reaction 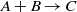 . In general, all chemical components are assumed to have different densities and viscosities, and a transverse velocity is introduced parallel to the interface between the reactants. Although the transverse flow is known for its stabilizing effect in viscously unstable non-reactive systems in the presence of an injection velocity, it is shown here that it can actually destabilize an initially stable reactive front. An expression for the critical transverse velocity beyond which an initially stable interface is destabilized is derived in the case of an initial sharp interface for reactants of the same viscosity. The analysis is extended to a diffused profile, and purely buoyancy-driven flows are analysed first in the absence of viscosity contrast and then in the presence of transverse flows and viscosity contrast. Various possible density fingering scenarios are determined based on the relative contribution of each chemical component to the density profile. It is found that the chemical reaction can destabilize a buoyancy-stable initial interface by generating a non-monotonic density profile. Unlike the viscous fingering of a reactive interface, a symmetry in the stability characteristics with respect to density increase or decrease by chemical reaction product is observed in the case of chemically buoyancy-driven flows for identical reactants.
. In general, all chemical components are assumed to have different densities and viscosities, and a transverse velocity is introduced parallel to the interface between the reactants. Although the transverse flow is known for its stabilizing effect in viscously unstable non-reactive systems in the presence of an injection velocity, it is shown here that it can actually destabilize an initially stable reactive front. An expression for the critical transverse velocity beyond which an initially stable interface is destabilized is derived in the case of an initial sharp interface for reactants of the same viscosity. The analysis is extended to a diffused profile, and purely buoyancy-driven flows are analysed first in the absence of viscosity contrast and then in the presence of transverse flows and viscosity contrast. Various possible density fingering scenarios are determined based on the relative contribution of each chemical component to the density profile. It is found that the chemical reaction can destabilize a buoyancy-stable initial interface by generating a non-monotonic density profile. Unlike the viscous fingering of a reactive interface, a symmetry in the stability characteristics with respect to density increase or decrease by chemical reaction product is observed in the case of chemically buoyancy-driven flows for identical reactants.

