Published online by Cambridge University Press: 27 April 2023
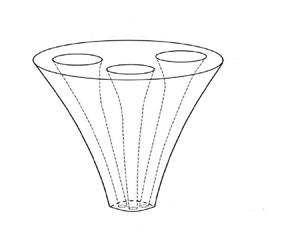
We consider the stability of the drawing of a long and thin viscous thread with an arbitrary number of internal holes of arbitrary shape that evolves due to axial drawing, inertia and surface tension effects. Despite the complicated geometry of the boundaries, we use asymptotic techniques to determine a particularly convenient formulation of the equations of motion that is well-suited to stability calculations. We will determine an explicit asymptotic solution for steady states with (a) large surface tension and negligible inertia, and (b) large inertia. In both cases, we will show that complicated boundary layer structures can occur. We will use linear stability analysis to show that the presence of an axisymmetric hole destabilises the flow for finite capillary number and which answers a question raised in the literature. However, our formulation allows us to go much further and consider arbitrary hole structures or non-axisymmetric shapes, and show that any structure with holes will be less stable than the case of a solid axisymmetric thread. For a solid axisymmetric thread, we will also determine a closed-form expression that delineates the unconditional instability boundary in which case the thread is unstable for all draw ratios. We will determine how the detailed effects of the microstructure affect the stability, and show that they manifest themselves only via a single function that occurs in the stability problem and hence have a surprisingly limited effect on the stability.