Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-29T19:06:46.978Z Has data issue: false hasContentIssue false
  • English
  • Français

Stability of an isolated pancake vortex in continuously stratified-rotating fluids

Published online by Cambridge University Press:  25 July 2016

Eunok Yim ,
Paul Billant  and
Claire Ménesguen
Eunok Yim*
Affiliation:
LadHyX, CNRS, École Polytechnique, F-91128 Palaiseau CEDEX, France
Paul Billant
Affiliation:
LadHyX, CNRS, École Polytechnique, F-91128 Palaiseau CEDEX, France
Claire Ménesguen
Affiliation:
LPO, IFREMER, CNRS, BP 70, 29280 Plouzané, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper investigates the stability of an axisymmetric pancake vortex with Gaussian angular velocity in radial and vertical directions in a continuously stratified-rotating fluid. The different instabilities are determined as a function of the Rossby number 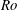$Ro$, Froude number 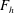$F_{h}$, Reynolds number 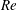$Re$ and aspect ratio ${\it\alpha}$. Centrifugal instability is not significantly different from the case of a columnar vortex due to its short-wavelength nature: it is dominant when the absolute Rossby number 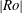$|Ro|$ is large and is stabilized for small and moderate 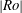$|Ro|$ when the generalized Rayleigh discriminant is positive everywhere. The Gent–McWilliams instability, also known as internal instability, is then dominant for the azimuthal wavenumber 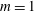$m=1$ when the Burger number 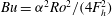$Bu={\it\alpha}^{2}Ro^{2}/(4F_{h}^{2})$ is larger than unity. When 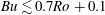$Bu\lesssim 0.7Ro+0.1$, the Gent–McWilliams instability changes into a mixed baroclinic–Gent–McWilliams instability. Shear instability for 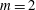$m=2$ exists when 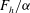$F_{h}/{\it\alpha}$ is below a threshold depending on 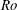$Ro$. This condition is shown to come from confinement effects along the vertical. Shear instability transforms into a mixed baroclinic–shear instability for small 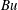$Bu$. The main energy source for both baroclinic–shear and baroclinic–Gent–McWilliams instabilities is the potential energy of the base flow instead of the kinetic energy for shear and Gent–McWilliams instabilities. The growth rates of these four instabilities depend mostly on 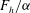$F_{h}/{\it\alpha}$ and 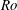$Ro$. Baroclinic instability develops when 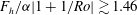$F_{h}/{\it\alpha}|1+1/Ro|\gtrsim 1.46$ in qualitative agreement with the analytical predictions for a bounded vortex with angular velocity slowly varying along the vertical.

JFM classification

Geophysical and Geological Flows: Geophysical and Geological Flows Vortex Flows: Vortex Flows Vortex Flows: Vortex instability
Type
Papers
Information
Journal of Fluid Mechanics , Volume 801 , 25 August 2016 , pp. 508 - 553
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abramowitz, M. & Stegun, I. A. 1972 Handbook of Mathematical Functions. Dover.Google Scholar
Antkowiak, A. & Brancher, P. 2004 Transient energy growth for the lamb-oseen vortex. Phys. Fluids 16, L1–L4.Google Scholar
Armi, L., Hebert, D., Oakey, N., Price, J. F., Richardson, P. L., Rossby, H. T. & Ruddick, B. 1989 Two years in the life of a mediterranean salt lens. J. Phys. Oceanogr. 19, 354–370.Google Scholar
Aubert, O., Le Bars, M., Le Gal, P. & Marcus, P. S. 2012 The universal aspect ratio of vortices in rotating stratified flows: experiments and observations. J. Fluid Mech. 706, 34–45.Google Scholar
Baey, J.-M. & Carton, X. 2002 Vortex multipoles in two-layer rotating shallow-water flows. J. Fluid Mech. 460, 151–175.Google Scholar
Balay, S., Abhyankar, S., Adams, M. F., Brown, J., Brune, P., Buschelman, K., Eijkhout, V., Gropp, W. D., Kaushik, D., Knepley, M. G. et al. 2014 PETSc users manual. Tech. Rep. ANL-95/11 – Revision 3.5. Argonne National Laboratory.CrossRefGoogle Scholar
Benilov, E. 2003 Instability of quasi-geostrophic vortices in a two-layer ocean with a thin upper layer. J. Fluid Mech. 475, 303–331.Google Scholar
Billant, P. 2010 Zigzag instability of vortex pairs in stratified and rotating fluids. Part 1. General stability equations. J. Fluid Mech. 660, 354–395.Google Scholar
Billant, P., Colette, A. & Chomaz, J.-M. 2004 Instabilities of a vortex pair in a stratified and rotating fluid. In Proceedings of the 21st International Congress of the International Union of Theoretical and Applied Mechanics, Varsovie, pp. 16–20. Springer.Google Scholar
Billant, P. & Gallaire, F. 2005 Generalized rayleigh criterion for non-axisymmetric centrifugal instabilities. J. Fluid Mech. 542, 365–379.CrossRefGoogle Scholar
Blumen, W. 1971 On the stability of a barotropic shear flow to nongeostrophic disturbances. Tellus 23 (4–5), 295–301.Google Scholar
Carton, X. 2001 Hydrodynamical modeling of oceanic vortices. Surv. Geophys. 22 (3), 179–263.Google Scholar
Carton, X., Le Cann, B., Serpette, A. & Dubert, J. 2013 Interactions of surface and deep anticyclonic eddies in the bay of biscay. J. Mar. Syst. 109–110, S45–S59; xII International Symposium on Oceanography of the Bay of Biscay.Google Scholar
Chang, K.-I., Teague, W. J., Lyu, S. J., Perkins, H. T., Lee, D.-K., Watts, D. R., Kim, Y.-B., Mitchell, D. A., Lee, C. M. & Kim, K. 2004 Circulation and currents in the southwestern east/japan sea: overview and review. Prog. Oceanogr. 61 (2–4), 105–156.CrossRefGoogle Scholar
Charney, J. G. & Stern, M. E. 1962 On the stability of internal baroclinic jets in a rotating atmosphere. J. Atmos. Sci. 19 (2), 159–172.2.0.CO;2>CrossRefGoogle Scholar
Dewar, W. K. & Killworth, P. D. 1995 On the stability of oceanic rings. J. Phys. Oceanogr. 25, 1467–1487.Google Scholar
Dewar, W. K., Killworth, P. D. & Blundell, J. R. 1999 Primitive-equation instability of wide oceanic rings. Part ii: numerical studies of ring stability. J. Phys. Oceanogr. 29, 1744–1758.Google Scholar
Drazin, P. G. & Reid, W. H. 1981 Hydrodynamic Stability. Cambridge Mathematical Library 1. Cambridge University Press.Google Scholar
Dritschel, D. G. & McKiver, W. J. 2015 Effect of prandtls ratio on balance in geophysical turbulence. J. Fluid Mech. 777, 569–590.Google Scholar
Dritschel, D. G., de la Torre Juárez, M. & Ambaum, M. H. P. 1999 The three-dimensional vortical nature of atmospheric and oceanic turbulent flows. Phys. Fluids 11 (6), 1512–1520.Google Scholar
Eady, E. T. 1949 Long waves and cyclone waves. Tellus 1 (3), 33–52.Google Scholar
Eliassen, A. 1983 The charney-stern theorem on barotropic-baroclinic instability. Pure Appl. Geophys. 121 (3), 563–572.Google Scholar
Eliassen, A. & Kleinschmidt, E. Jr. 1957 Dynamic meteorology. In Geophysik II/Geophysics II (ed. Bartels, Julius), Handbuch der Physik/Encyclopedia of Physics, vol. 10/48, pp. 1–154. Springer.Google Scholar
Flierl, G. R. 1988 On the instability of geostrophic vortices. J. Fluid Mech. 197, 349–388.Google Scholar
Ford, R. 1994 The instability of an axisymmetric vortex with monotonic potential vorticity in rotating shallow water. J. Fluid Mech. 280, 303–334.Google Scholar
Garnaud, X.2012 Modes, transient dynamics and forced response of circular jets. PhD thesis, LadHyX, Ecole Polytechnique X.Google Scholar
Garnaud, X., Lesshafft, L., Schmid, P. J. & Huerre, P. 2013 Modal and transient dynamics of jet flows. Phys. Fluids 25 (4), 044103.Google Scholar
Gent, P. R. & McWilliams, J. C. 1986 The instability of barotropic circular vortices. Geophys. Astrophys. Fluid Dyn. 35 (1–4), 209–233.CrossRefGoogle Scholar
Gill, A. E. 1981 Homogeneous intrusions in a rotating stratified fluid. J. Fluid Mech. 103, 275–295.CrossRefGoogle Scholar
Griffiths, R. W. & Linden, P. F. 1981 The stability of vortices in a rotating, stratified fluid. J. Fluid Mech. 105, 283–316.CrossRefGoogle Scholar
Hassanzadeh, P., Marcus, P. S. & Le Gal, P. 2012 The universal aspect ratio of vortices in rotating stratified flows: theory and simulation. J. Fluid Mech. 706, 46–57.Google Scholar
Hecht, F. 2012 New development in freefem++. J. Numer. Math. 20 (3–4), 251–265.Google Scholar
Hedstrom, K. & Armi, L. 1988 An experimental study of homogeneous lenses in a stratified rotating fluid. J. Fluid Mech. 191, 535–556.Google Scholar
Helfrich, K. R. & Send, U. 1988 Finite-amplitude evolution of two-layer geostrophic vortices. J. Fluid Mech. 197, 331–348.Google Scholar
Hernandez, V., Roman, J. E. & Vidal, V. 2005 SLEPc: a scalable and flexible toolkit for the solution of eigenvalue problems. ACM Trans. Math. Softw. 31 (3), 351–362.Google Scholar
Hide, R. & Mason, P. J. 1975 Sloping convection in a rotating fluid. Adv. Phys. 24 (1), 47–100.Google Scholar
Hobbs, R. 2007 Go (geophysical oceanography): a new tool to understand the thermal structure and dynamics of oceans. European Union Newsletter 2, 7.Google Scholar
Hopfinger, E. J. & van Heijst, G. J. F. 1993 Vortices in rotating fluids. Annu. Rev. Fluid Mech. 25 (1), 241–289.CrossRefGoogle Scholar
Hoskins, B. J., McIntyre, M. E. & Robertson, A. W. 1985 On the use and significance of isentropic potential vorticity maps. Q. J. R. Meteorol. Soc. 111 (470), 877–946.Google Scholar
Hua, B. L., Ménesguen, C., Le Gentil, S., Schopp, R., Marsset, B. & Aiki, H. 2013 Layering and turbulence surrounding an anticyclonic oceanic vortex: in situ observations and quasi-geostrophic numerical simulations. J. Fluid Mech. 731, 418–442.Google Scholar
Ikeda, M. 1981 Instability and splitting of mesoscale rings using a two-layer quasi-geostrophic model on an f-plane. J. Phys. Oceanogr. 11 (7), 987–998.Google Scholar
Killworth, P. D., Blundell, J. R. & Dewar, W. K. 1997 Primitive equation instability of wide oceanic rings. Part i: linear theory. J. Phys. Oceanogr. 27, 941–962.2.0.CO;2>CrossRefGoogle Scholar
Kim, D., Yang, E., Kim, K., Shin, C., Park, J., Yoo, S. & Hyun, J. 2012 Impact of an anticyclonic eddy on the summer nutrient and chlorophyll a distributions in the ulleung basin, east sea (Japan sea). J. Mar. Syst. 69 (1), 23–29.Google Scholar
Lahaye, N. & Zeitlin, V. 2015 Centrifugal, barotropic and baroclinic instabilities of isolated ageostrophic anticyclones in the two-layer rotating shallow water model and their nonlinear saturation. J. Fluid Mech. 762, 5–34.Google Scholar
Lazar, A., Stegner, A., Caldeira, R., Dong, C., Didelle, H. & Viboud, S. 2013a Inertial instability of intense stratified anticyclones. Part 2. Laboratory experiments. J. Fluid Mech. 732, 485–509.CrossRefGoogle Scholar
Lazar, A., Stegner, A. & Heifetz, E. 2013b Inertial instability of intense stratified anticyclones. Part 1. Generalized stability criterion. J. Fluid Mech. 732, 457–484.Google Scholar
McIntyre, M. E. 1970 Diffusive destabilization of the baroclinic circular vortex. Geophys. Fluid Dyn. 1, 19–57.Google Scholar
Ménesguen, C., Hua, B. L., Carton, X., Klingelhoefer, F., Schnrle, P. & Reichert, C. 2012a Arms winding around a meddy seen in seismic reflection data close to the morocco coastline. Geophys. Res. Lett. 39 (5), L05604.Google Scholar
Ménesguen, C., McWilliams, J. C. & Molemaker, M. J. 2012b Ageostrophic instability in a rotating stratified interior jet. J. Fluid Mech. 711, 599–619.Google Scholar
Meschanov, S. L. & Shapiro, G. I. 1998 A young lens of red sea water in the arabian sea. Deep-Sea Res. I 45 (1), 1–13.Google Scholar
Negretti, M. E. & Billant, P. 2013 Stability of a gaussian pancake vortex in a stratified fluid. J. Fluid Mech. 718, 457–480.Google Scholar
Nguyen, H. Y., Hua, B. L., Schopp, R. & Carton, X. 2012 Slow quasigeostrophic unstable modes of a lens vortex in a continuously stratified flow. Geophys. Astrophys. Fluid Dyn. 106 (3), 305–319.Google Scholar
Pingree, R. D. & Le Cann, B. 1992 Anticyclonic eddy x91 in the southern bay of biscay, May 1991–February 1992. J. Geophys. Res. 97 (C9), 14353–14367.Google Scholar
Reinaud, J. N., Dritschel, D. G. & Koudella, C. R. 2003 The shape of vortices in quasi-geostrophic turbulence. J. Fluid Mech. 474, 175–192.Google Scholar
Richardson, P. L., Bower, A. S. & Zenk, W. 2000 A census of meddies tracked by floats. Prog. Oceanogr. 45, 209–250.Google Scholar
Riedinger, X., Le Dizès, S. & Meunier, P. 2010 Viscous stability properties of a lamb-oseen vortex in a stratified fluid. J. Fluid Mech. 645, 255–278.Google Scholar
Ripa, P. 1991 General stability conditions for a multi-layer model. J. Fluid Mech. 222, 119–137.Google Scholar
Roman, J. E., Campos, C., Romero, E. & Tomas, A.2015 SLEPc users manual. Tech. Rep. DSIC-II/24/02 – Revision 3.6. D. Sistemes Informàtics i Computació, Universitat Politècnica de València.Google Scholar
Saunders, P. M. 1973 The instability of a baroclinic vortex. J. Phys. Oceanogr. 3, 61–65.Google Scholar
Smyth, W. D. & McWilliams, J. C. 1998 Instability of an axisymmetric vortex in a stably stratified, rotating environment. Theor. Comput. Fluid Dyn. 11 (3–4), 305–322.CrossRefGoogle Scholar
Solberg, H. 1936 Le mouvement d’inertie de l’atmosphère stable et son rôle dans la théorie des cyclones. In Meteor. Assoc. U.G.G.I., pp. 66–82. Dupont.Google Scholar
Stegner, A. & Dritschel, D. G. 2000 A numerical investigation of the stability of isolated shallow water vortices. J. Phys. Oceanogr. 30, 2562–2573.Google Scholar
Thivolle-Cazat, J., Sommeria, J. & Galmiche, M. 2005 Baroclinic instability of two-layer vortices in laboratory experiments. J. Fluid Mech. 544, 69–97.Google Scholar
Vallis, G. K. 2006 Atmospheric and Oceanic Fluid Dynamics: Fundamentals and Large-scale Circulation. Cambridge University Press.Google Scholar
Verzicco, R., Lalli, F. & Campana, E. 1997 Dynamics of baroclinic vortices in a rotating, stratified fluid: a numerical study. Phys. Fluids 9 (2), 419–432.Google Scholar
Yim, E. & Billant, P. 2015 On the mechanism of the Gent–McWilliams instability of a columnar vortex in stratified rotating fluids. J. Fluid Mech. 780, 5–44.Google Scholar
Yim, E. & Billant, P. 2016 Analogies and differences between the stability of an isolated pancake vortex and a columnar vortex in stratified fluid. J. Fluid Mech. 796, 732–766.Google Scholar