Article contents
Stability influences on interscale transport of turbulent kinetic energy and Reynolds shear stress in atmospheric boundary layers interacting with a tall vegetation canopy
Published online by Cambridge University Press: 29 June 2021
Abstract
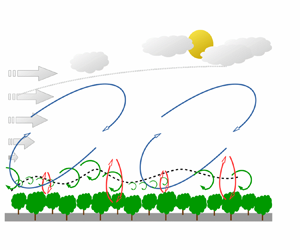
High-resolution data from the large-eddy simulation of the atmospheric boundary layer (ABL) over a vegetation canopy are used to investigate the interaction between the most energetic large-scale structures from the ABL and the smaller scales from the near-canopy region. First, evidence of amplitude modulation (AM) involving the three velocity components is demonstrated. A multi-scale analysis of the transport equation of both the turbulent kinetic energy (TKE) and Reynolds shear stress (RSS) is then performed using a multi-level filtering procedure. It is found that, on average, in the investigated region, large scales are a source of TKE for the small scales (e.g. forward scatter of TKE) through nonlinear interscale transfer ( $T_r^L$) with a maximum at canopy top while they are a sink via turbulent transport (
$T_r^L$) with a maximum at canopy top while they are a sink via turbulent transport ( $T_t^L$). Close to the canopy, the small-scale RSS transport behaves the same while, above the roughness sublayer,
$T_t^L$). Close to the canopy, the small-scale RSS transport behaves the same while, above the roughness sublayer,  $T_r^L$ and
$T_r^L$ and  $T_t^L$ switch roles showing the existence of RSS backscatter. The standard deviation of the transfer terms shows that there are intense instantaneous forward and backscatter of both TKE and RSS via all the transfer terms. It is therefore demonstrated that there is a two-way coupling between the ABL and the near-canopy scales, the well-known top-down mechanism through TKE transfer being complemented by a bottom-up feedback through RSS transfer. This analysis is extended to several stability regimes, confirming the above conclusions and showing the increasing role of the large-scale wall-normal component in AM and TKE or RSS transfers when the flow becomes buoyancy driven.
$T_t^L$ switch roles showing the existence of RSS backscatter. The standard deviation of the transfer terms shows that there are intense instantaneous forward and backscatter of both TKE and RSS via all the transfer terms. It is therefore demonstrated that there is a two-way coupling between the ABL and the near-canopy scales, the well-known top-down mechanism through TKE transfer being complemented by a bottom-up feedback through RSS transfer. This analysis is extended to several stability regimes, confirming the above conclusions and showing the increasing role of the large-scale wall-normal component in AM and TKE or RSS transfers when the flow becomes buoyancy driven.
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press
References
REFERENCES
- 9
- Cited by



