Published online by Cambridge University Press: 06 March 2012
A Batchelor vortex represents the asymptotic solution of a trailing vortex in an aircraft wake. In this study, an unequal-strength, counter-rotating Batchelor vortex pair is employed as a model of the wake emanating from one side of an aircraft wing; this model is a direct extension of several prior investigations that have considered unequal-strength Lamb–Oseen vortices as representations of the aircraft wake problem. Both solution of the linearized Navier–Stokes equations and direct numerical simulations are employed to study the linear and nonlinear development of a vortex pair with a circulation ratio of 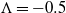 . In contrast to prior investigations considering a Lamb–Oseen vortex pair, we note strong growth of the Kelvin mode
. In contrast to prior investigations considering a Lamb–Oseen vortex pair, we note strong growth of the Kelvin mode 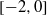 coupled with an almost equal growth rate of the Crow instability. Three stages of nonlinear instability development are defined. In the initial stage, the Kelvin mode amplitude becomes sufficiently large that oscillations within the core of the weaker vortex are easily observable and significantly affect the profile of the weaker vortex. In the secondary stage, filaments of secondary vorticity emanate from the weaker vortex and are convected around the stronger vortex. In the tertiary stage, a transition in the dominant instability wavelength is observed from the short-wavelength Kelvin mode to the longer-wavelength Crow instability. Much of the instability growth is observed on the weaker vortex of the pair, although small perturbations in the stronger vortex are observed in the tertiary nonlinear growth phase.
coupled with an almost equal growth rate of the Crow instability. Three stages of nonlinear instability development are defined. In the initial stage, the Kelvin mode amplitude becomes sufficiently large that oscillations within the core of the weaker vortex are easily observable and significantly affect the profile of the weaker vortex. In the secondary stage, filaments of secondary vorticity emanate from the weaker vortex and are convected around the stronger vortex. In the tertiary stage, a transition in the dominant instability wavelength is observed from the short-wavelength Kelvin mode to the longer-wavelength Crow instability. Much of the instability growth is observed on the weaker vortex of the pair, although small perturbations in the stronger vortex are observed in the tertiary nonlinear growth phase.