Hostname: page-component-745bb68f8f-b6zl4 Total loading time: 0 Render date: 2025-01-09T22:00:28.062Z Has data issue: false hasContentIssue false
  • English
  • Français

Stability and three-dimensional evolution of a transitional dynamic stall vortex

Published online by Cambridge University Press:  15 June 2017

Abel-John Buchner Open the ORCID record for Abel-John Buchner [Opens in a new window] ,
Damon Honnery  and
Julio Soria Open the ORCID record for Julio Soria [Opens in a new window]
Abel-John Buchner*
Affiliation:
Laboratory for Turbulence Research in Aerospace and Combustion, Department of Mechanical and Aerospace Engineering, Monash University, Melbourne, VIC 3800, Australia
Damon Honnery
Affiliation:
Laboratory for Turbulence Research in Aerospace and Combustion, Department of Mechanical and Aerospace Engineering, Monash University, Melbourne, VIC 3800, Australia
Julio Soria
Affiliation:
Laboratory for Turbulence Research in Aerospace and Combustion, Department of Mechanical and Aerospace Engineering, Monash University, Melbourne, VIC 3800, Australia Department of Aeronautical Engineering, King Abdulaziz University, Jeddah, Kingdom of Saudi Arabia
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper describes a series of experiments using particle image velocimetry to investigate the dynamic stall resulting due to a rapid pitching motion of a flat plate. There exist in such unsteady separated flows multiple time-dependent coherent structures, whose interaction and evolution are complex and nonlinear. 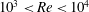The experiments presented here are aimed at determining the behaviour of a dynamic stall vortex system in the Reynolds number range $10^{3}<Re<10^{4}$. Evidence is presented for the development of the three-dimensional structure associated with the dynamic stall vortex and its interaction with the no-slip boundary condition at the surface of the pitching plate. The analysis presented suggests that a centrifugal instability exists, and that the form of the three-dimensional structure is consistent with that expected of a centrifugal instability. The structure and scale dependence of the flow are explored using wavelet and Fourier methods, with the dependence of the flow on Reynolds number examined, as well as the influence of spanwise end boundary conditions.

JFM classification

Instability: Instability Instability: Transition to turbulence Vortex Flows: Vortex Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 823 , 25 July 2017 , pp. 166 - 197
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Anderson, J. D. 2011 Fundamentals of Aerodynamics. McGraw–Hill.Google Scholar
Baik, Y. S. & Bernal, L. P. 2012 Experimental study of pitching and plunging airfoils at low Reynolds numbers. Exp. Fluids 53, 1979–1992.CrossRefGoogle Scholar
Baik, Y. S., Bernal, L. P., Granlund, K. & Ol, M. V. 2012 Unsteady force generation and vortex dynamics of pitching and plunging aerofoils. J. Fluid Mech. 709, 37–68.CrossRefGoogle Scholar
Bayly, B. J. 1988 Three-dimensional centrifugal-type instabilities in inviscid two-dimensional flows. Phys. Fluids 31, 56–64.CrossRefGoogle Scholar
Brennen, C. E.1982 A review of added mass and fluid inertial forces. Tech. Rep., CR-82.010, Naval Civil Engineering Laboratory.Google Scholar
Buchner, A.-J., Buchmann, N. A., Kilany, K., Atkinson, C. H. & Soria, J. 2012 Stereoscopic and tomographic PIV of a pitching plate. Exp. Fluids 52, 299–314.CrossRefGoogle Scholar
Buchner, A.-J., Lohry, M. W., Martinelli, L., Soria, J. & Smits, A. J. 2015a Dynamic stall in vertical axis wind turbines: comparing experiments and computations. J. Wind Engng Ind. Aerodyn. 146, 163–171.CrossRefGoogle Scholar
Buchner, A.-J., Smits, A. J. & Soria, J. 2014 Scaling of vertical axis wind turbine dynamic stall. In 19th Australasian Fluid Mechanics Conference, Melbourne, Australia. AFMS.Google Scholar
Buchner, A.-J. & Soria, J. 2014 Measurements of the flow due to a rapidly pitching plate using time resolved high resolution PIV. Aerosp. Sci. Technol. 44, 4–17.CrossRefGoogle Scholar
Buchner, A.-J., Soria, J. & Smits, A. J. 2015b Circulation production and shedding from vertical axis wind turbine blades undergoing dynamic stall. In 9th International Symposium on Turbulence and Shear Flow Phenomena, Melbourne, Australia. TSFP. Available at: http://www.tsfp-conference.org/proceedings/proceedings-of-tsfp-9-2015-melbourne.html.Google Scholar
Canals, M. & Pawlak, G. 2011 Three-dimensional vortex dynamics in oscillatory flow separation. J. Fluid Mech. 674, 408–432.CrossRefGoogle Scholar
Carr, L. W. 1988 Progress in analysis and prediction of dynamic stall. J. Aircraft 25 (1), 6–17.CrossRefGoogle Scholar
Conger, R. N. & Ramaprian, B. R. 1994 Pressure measurements on a pitching airfoil in a water channel. AIAA J. 32 (1), 108–115.CrossRefGoogle Scholar
Daubechies, I. 1988 Orthonormal bases of compactly supported wavelets. Commun. Pure Appl. Maths 41, 909–996.CrossRefGoogle Scholar
Eldredge, J. D., Chengjie, W. & Ol, M. V. 2009 A computational study of a canonical pitch-up, pitch-down wing maneuver. In 39th AIAA Fluid Dynamics Conference, San Antonio, Texas, AIAA2009-3687. AIAA.Google Scholar
Ellington, C. P., Van den Berg, C., Willmott, A. P. & Thomas, A. L. R. 1996 Leading edge vortices in insect flight. Nature 384, 626–630.CrossRefGoogle Scholar
Eslam Panah, A., Akkala, J. M. & Buchholz, J. H. J. 2015 Vorticity transport and the leading edge vortex of a plunging airfoil. Exp. Fluids 56 (8), 160.CrossRefGoogle Scholar
Ferreira, C. S., van Kuik, G., van Bussel, G. & Scarano, F. 2009 Visualisation by PIV of dynamic stall on a vertical axis wind turbine. Exp. Fluids 46, 97–108.CrossRefGoogle Scholar
Garmann, D. J. & Visbal, M. R. 2011 Numerical investigation of transitional flow over a rapidly pitching plate. Phys. Fluids 23, 094106.CrossRefGoogle Scholar
Gendrich, C. P., Koochesfahani, M. M. & Visbal, M. R. 1995 Effects of initial acceleration on the flow field development around rapidly pitching airfoils. Trans. ASME J. Fluids Engng 117 (1), 45–49.CrossRefGoogle Scholar
Görtler, H. 1954 On the three-dimensional instability of laminar boundary layers on concave walls. In NACA Technical Memorandum 1375.Google Scholar
Ham, N. D. & Garelick, M. S. 1968 Dynamic stall considerations in helicopter rotors. J. Am. Helicopter Society 13 (2), 49–55.CrossRefGoogle Scholar
Harris, F. D. & Pruyn, R. R. 1968 Blade stall – half fact, half fiction. J. Am. Helicopter Society 13 (2), 27–48.CrossRefGoogle Scholar
Katul, G. G. & Parlange, M. B. 1994 The spatial structure of turbulence at production wavenumbers using orthonormal wavelets. Boundary-Layer Meteorol. 75 (1), 81–108.CrossRefGoogle Scholar
Koochesfahani, M. M. & Smiljanovski, V. 1992 Effect of initial acceleration on the development of the flow field of an airfoil pitching at constant rate. In Proceedings of NASA/AFOSR/ARO Workshop on Physics of Forced Unsteady Separation, NASA Ames Research Center, pp. 317–332.Google Scholar
Koochesfahani, M. M. & Smiljanovski, V. 1993 Initial acceleration effects on flow evolution around airfoils pitching to high angles of attack. AIAA J. 31 (8), 1529–1531.CrossRefGoogle Scholar
Lang, J. D. & Francis, M. S. 1985 Unsteady aerodynamics and dynamic aircraft maneuverability. In NATO Advisory Group for Aerospace Research and Development (AGARD) Technical Meeting on Unsteady Aerodynamics – Fundamentals and Applications to Aircraft Dynamics, May 6–9. Paper No. A29. NATO.Google Scholar
Larsen, J. W., Nielsen, S. R. K. & Krenk, S. 2007 Dynamic stall model for wind turbine airfoils. J. Fluids Struct. 23, 959–982.CrossRefGoogle Scholar
Li, H., Takei, M., Ochi, M., Saito, Y. & Horii, K. 1999 Structure evaluation of unsteady turbulent flow with continuous and discrete wavelet transforms. In 3rd ASME/JSME Joint Fluids Engineering Conference, San Francisco, California, FEDSM99-7167. ASME.Google Scholar
Mallat, S. 1989 A theory for multiresolution signal decomposition: the wavelet representation. IEEE Trans. Pattern Anal. Mach. Intell. 11, 674–693.CrossRefGoogle Scholar
McCroskey, W. 1982 Unsteady airfoils. Annu. Rev. Fluid Mech. 14, 285–311.CrossRefGoogle Scholar
McCroskey, W. J., Carr, L. W. & McAlister, K. W. 1976 Dynamic stall experiments on oscillating airfoils. AIAA J. 14 (1), 57–63.CrossRefGoogle Scholar
Newland, D. E. 1995 An Introduction to Random Vibrations, Spectral and Wavelet Analaysis, 3rd edn. Longman Scientific and Technical.Google Scholar
Ol, M. V. 2009 The high-frequency, high-amplitude pitch problem: airfoils, plates and wings. In 39th AIAA Fluid Dynamics Conference, San Antonio, Texas, AIAA2009-3686. AIAA.Google Scholar
Ol, M. V., Altman, A., Eldredge, J. D., Garmann, D. J. & Lian, Y. 2010 Resume of the AIAA FDTC low Reynolds number discussion group’s canonical cases. In 48th AIAA Aerospace Sciences Meeting, Orlando, Florida, AIAA2010-1085. AIAA.Google Scholar
Ol, M. V., Bernal, L., Kang, C.-K. & Shyy, W. 2009a Shallow and deep dynamic stall for flapping low Reynolds number airfoils. Exp. Fluids 46 (5), 883–901.CrossRefGoogle Scholar
Ol, M. V., Eldredge, J. D. & Wang, C. 2009b High-amplitude pitch of a flat plate: an abstraction of perching and flapping. Intl J. Micro Air Vehicles 1 (3), 33–48.CrossRefGoogle Scholar
Qian, S. & Weiss, J. 1993 Wavelets and the numerical solution of boundary value problems. Appl. Maths. Lett. 6 (1), 47–52.CrossRefGoogle Scholar
Raffel, M., Willert, C., Wereley, S. & Kompenhans, J. 2007 Particle Image Velocimetry: A Practical Guide, 2nd edn. Springer.CrossRefGoogle Scholar
Ramesh, K., Gopalarathnam, A., Granlund, K., Ol, M. V. & Edwards, J. R. 2014 Discrete-vortex method with novel shedding criterion for unsteady aerofoil flows with intermittent leading-edge vortex shedding. J. Fluid Mech. 751, 500–538.CrossRefGoogle Scholar
Rayleigh, Lord 1917 On the dynamics of revolving flows. Proc. R. Soc. Lond. A 93, 148–154.Google Scholar
Robinson, M. C. & Wissler, J. B. 1988 Pitch rate and Reynolds number effects on a pitching rectangular wing. In 6th Applied Aerodynamics Conference, Williamsburg, Virginia. AIAA Paper 88-2577-CP. AIAA.Google Scholar
Shreck, S. J., Faller, W. E. & Helin, H. E. 1998 Pitch rate and Reynolds number effects on unsteady boundary-layer transition and separation. J. Aircraft 35 (1), 46–52.CrossRefGoogle Scholar
Shreck, S. J., Faller, W. E. & Robinson, M. C. 2002 Unsteady separation rocesses and leading edge vortex precursors: pitch rate and Reynolds number influences. J. Aircraft 39 (5), 868–875.CrossRefGoogle Scholar
Shyy, W., Lian, Y., Tang, J., Viieru, D. & Liu, H. 2008 Aerodynamics of Low Reynolds Number Flyers. Cambridge University Press.Google Scholar
Sipp, D. & Jacquin, L. 2000 Three-dimensional centrifugal-type instabilities of two-dimensional flows in rotating systems. Phys. Fluids 12 (7), 1740–1748.CrossRefGoogle Scholar
Soria, J. 1996 An investigation of the near wake of a circular cylinder using a video-based digital cross-correlation particle image velocimetry technique. Exp. Therm. Fluid Sci. 12 (2), 221–233.CrossRefGoogle Scholar
Soria, J., Cater, J. & Kostas, J. 1999 High resolution multigrid cross-correlation digital PIV measurements of a turbulent starting jet using half frame image shift film recording. Opt. Laser Technol 31, 3–12.CrossRefGoogle Scholar
Soria, J., New, T. H., Lim, T. T. & Parker, K. 2003 Multigrid CCDPIV measurements of accelerated flow past an airfoil at an angle of attack of 30° . Exp. Therm. Fluid Sci. 27, 667–676.CrossRefGoogle Scholar
Strang, G. 1989 Wavelets and dilation equations: a brief introduction. SIAM Rev. 31 (4), 614–627.CrossRefGoogle Scholar
Strang, G. & Fix, G. 1973 A Fourier Analysis of the Finite Element Variational Method. Edizioni Cremonese.Google Scholar
Theisel, H.1995 Vector field curvature and applications. PhD thesis, Universität Rostock.Google Scholar
Visbal, M. 2009 High-fidelity simulation of transitional flows past a plunging airfoil. AIAA J. 47 (11).CrossRefGoogle Scholar
Weng, H. & Lau, K-M. 1994 Wavelets, period doubling, and time frequency localization with application to organization of convection over the tropical western Pacific. J. Atmos. Sci. 51 (17), 2523–2541.2.0.CO;2>CrossRefGoogle Scholar
Williamson, C. H. K. 1996 Vortex dynamics in the cylinder wake. Annu. Rev. Fluid Mech. 28, 477–539.CrossRefGoogle Scholar
Wu, J., Sheridan, J., Soria, J. & Welsh, M. C. 1994 An exerimental investigation of streamwise vortices in the wake of a bluff body. J. Fluids Struct. 8, 621–625.CrossRefGoogle Scholar