Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-29T14:14:52.676Z Has data issue: false hasContentIssue false
  • English
  • Français

Stability and resonant wave interactions of confined two-layer Rayleigh–Bénard systems

Published online by Cambridge University Press:  06 August 2014

S. V. Diwakar ,
Shaligram Tiwari ,
Sarit K. Das  and
T. Sundararajan
S. V. Diwakar
Affiliation:
Department of Mechanical Engineering, Indian Institute of Technology Madras, Chennai 600036, India
Shaligram Tiwari
Affiliation:
Department of Mechanical Engineering, Indian Institute of Technology Madras, Chennai 600036, India
Sarit K. Das
Affiliation:
Department of Mechanical Engineering, Indian Institute of Technology Madras, Chennai 600036, India
T. Sundararajan*
Affiliation:
Department of Mechanical Engineering, Indian Institute of Technology Madras, Chennai 600036, India
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The current work analyses the onset characteristics of Rayleigh–Bénard convection in confined two-dimensional two-layer systems. Owing to the interfacial interactions and the possibilities of convection onset in the individual layers, the two-layer systems typically exhibit diverse excitation modes. While the attributes of these modes range from the non-oscillatory mechanical/thermal couplings to the oscillatory standing/travelling waves, their regimes of occurrence are determined by the numerous system parameters and property ratios. In this regard, the current work aims at characterising their respective influence via methodical linear and fully nonlinear analyses, carried out on fluid systems that have been selected using the concept of balanced contrasts. Consequently, the occurrence of oscillatory modes is found to be associated with certain favourable fluid combinations and interfacial heights. The further branching of oscillatory modes into standing and travelling waves seems to additionally rely on the aspect ratio of the confined cavity. Specifically, the modulated travelling waves have been observed to occur (amidst standing wave modes) at discrete aspect ratios for which the onset of oscillatory convection happens at unequal fluid heights. This behaviour corresponds to the typical 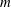$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}m$:$n$ resonance where the critical wavenumbers of convection onset in the layers are dissimilar. Based on all of these observations, an attempt has been made in the present work to identify the oscillatory excitation modes with a reduced number of non-dimensional parameters.

JFM classification

Convection: Buoyancy-driven instability Convection: Convection in cavities
Type
Papers
Information
Journal of Fluid Mechanics , Volume 754 , 10 September 2014 , pp. 415 - 455
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Busse, F. H. 1981 On the aspect ratios of two-layer mantle convection. Phys. Earth Planet. Inter. 24 (4), 320–324.CrossRefGoogle Scholar
Chorin, A. J. 1968 Numerical solution of the Navier–Stokes equations. Maths Comput. 22 (104), 745–762.CrossRefGoogle Scholar
Colinet, P. & Legros, J. C. 1994 On the Hopf bifurcation occurring in the two-layer Rayleigh–Bénard convective instability. Phys. Fluids 6, 2631–2639.CrossRefGoogle Scholar
Colinet, P., Legros, J. C. & Velarde, M. G. 2001 Nonlinear Dynamics of Surface-Tension-Driven Instabilities. Wiley-VCH.CrossRefGoogle Scholar
Degen, M. M., Colovas, P. W. & Andereck, C. D. 1998 Time-dependent patterns in the two-layer Rayleigh–Bénard system. Phys. Rev. E 57 (6), 6647–6659.CrossRefGoogle Scholar
Dennis, S. C. R. & Quartapelle, L. 1983 Direct solution of the vorticity-stream function ordinary differential equations by a Chebyshev approximation. J. Comput. Phys. 52 (3), 448–463.CrossRefGoogle Scholar
Diwakar, S. V., Das, S. K. & Sundararajan, T. 2014 Accurate solutions of Rayleigh Bénard convection in confined two layer systems using spectral domain decomposition method. Numer. Heat Transfer A; 10.1080/10407782.2014.901048.Google Scholar
Gottlieb, D. & Shu, C. W. 1997 On the Gibbs phenomenon and its resolution. SIAM Rev. 39 (4), 644–668.CrossRefGoogle Scholar
Hewitt, E. & Hewitt, R. E. 1979 The Gibbs–Wilbraham phenomenon: an episode in Fourier analysis. Arch. Hist. Exact Sci. 21 (2), 129–160.Google Scholar
Johnson, E. S. 1975 Liquid encapsulated floating zone melting of gaas. J. Cryst. Growth 30 (2), 249–256.Google Scholar
Johnson, D. & Narayanan, R. 1996 Experimental observation of dynamic mode switching in interfacial-tension-driven convection near a codimension-two point. Phys. Rev. E 54 (4), 3102–3104.Google Scholar
Johnson, D. & Narayanan, R. 1997 Geometric effects on convective coupling and interfacial structures in bilayer convection. Phys. Rev. E 56 (5), 5462–5472.Google Scholar
Nataf, H. C., Moreno, S. & Cardin, P. 1988 What is responsible for thermal coupling in layered convection? J. Phys. 49 (10), 1707–1714.Google Scholar
Nepomnyashchy, A. A. & Simanovskii, I. B. 2004 Influence of thermocapillary effect and interfacial heat release on convective oscillations in a two-layer system. Phys. Fluids 16, 1127–1139.CrossRefGoogle Scholar
Rasenat, S., Busse, F. H. & Rehberg, I. 1989 A theoretical and experimental study of double-layer convection. J. Fluid Mech. 199, 519–540.CrossRefGoogle Scholar
Renardy, Y. Y. 1996 Pattern formation for oscillatory bulk-mode competition in a two-layer Bénard problem. Z. Angew. Math. Phys. 47 (4), 567–590.CrossRefGoogle Scholar
Renardy, Y. Y., Renardy, M. & Fujimura, K. 1999 Takens–Bogdanov bifurcation on the hexagonal lattice for double-layer convection. Physica D 129 (3), 171–202.CrossRefGoogle Scholar
Richter, F. M. & Johnson, C. E. 1974 Stability of a chemically layered mantle. J. Geophys. Res. 79 (11), 1635–1639.CrossRefGoogle Scholar
Sabbah, C. & Pasquetti, R. 1998 A divergence-free multidomain spectral solver of the Navier–Stokes equations in geometries of high aspect ratio. J. Comput. Phys. 139 (2), 359–379.CrossRefGoogle Scholar
Shen, Y., Neitzel, G. P., Jankowski, D. F. & Mittelmann, H. D. 1990 Energy stability of thermocapillary convection in a model of the float-zone crystal-growth process. J. Fluid Mech. 217 (1), 639–660.CrossRefGoogle Scholar
Simanovskii, I. B. & Nepomnyashchy, A. A. 2006 Nonlinear development of oscillatory instability in a two-layer system under the combined action of buoyancy and thermocapillary effect. J. Fluid Mech. 555, 177–202.Google Scholar
Xie, Yi.-C. & Xia, Ke.-Q. 2013 Dynamics and flow coupling in two-layer turbulent thermal convection. J. Fluid Mech. 728 (R1), 1–14.Google Scholar
Zeren, R. W. & Reynolds, W. C. 1972 Thermal instabilities in two-fluid horizontal layers. J. Fluid Mech. 53 (2), 305–327.CrossRefGoogle Scholar

Diwakar et al. supplementary material

Onset of standing wave oscillations in a two layer system with a*=0.667, ρβα = 4.0 and AR = 2.35

Download Diwakar et al. supplementary material(Video)
Video 5.8 MB

Diwakar et al. supplementary material

Onset of standing wave oscillations in a two layer system with a*=0.667, ρβα = 4.0 and AR = 2.45

Download Diwakar et al. supplementary material(Video)
Video 8.3 MB

Diwakar et al. supplementary material

Onset of quasi-periodic modulated travelling waves in a two layer system with a*=0.667, ρβα = 4.0 and AR = 2.415

Download Diwakar et al. supplementary material(Video)
Video 25.9 MB