Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-23T15:31:49.394Z Has data issue: false hasContentIssue false
  • English
  • Français

Stabilisation and drag reduction of pipe flows by flattening the base profile

Published online by Cambridge University Press:  28 January 2019

Elena Marensi Open the ORCID record for Elena Marensi [Opens in a new window] ,
Ashley P. Willis Open the ORCID record for Ashley P. Willis [Opens in a new window]  and
Rich R. Kerswell
Elena Marensi*
Affiliation:
School of Mathematics and Statistics, University of Sheffield, Sheffield S3 7RH, UK
Ashley P. Willis
Affiliation:
School of Mathematics and Statistics, University of Sheffield, Sheffield S3 7RH, UK
Rich R. Kerswell
Affiliation:
Department of Applied Mathematics and Theoretical Physics, Centre for Mathematical Sciences, University of Cambridge, Cambridge CB3 0WA, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Recent experimental observations (Kühnen et al., Nat. Phys., vol. 14, 2018b, pp. 386–390) have shown that flattening a turbulent streamwise velocity profile in pipe flow destabilises the turbulence so that the flow relaminarises. We show that a similar phenomenon exists for laminar pipe flow profiles in the sense that the nonlinear stability of the laminar state is enhanced as the profile becomes more flattened. The flattening of the laminar base profile is produced by an artificial localised body force designed to mimic an obstacle used in the experiments of Kühnen et al. (Flow Turbul. Combust., vol. 100, 2018a, pp. 919–943) and the nonlinear stability measured by the size of the energy of the initial perturbations needed to trigger transition. Significant drag reduction is also observed for the turbulent flow when triggered by sufficiently large disturbances. In order to make the nonlinear stability computations more efficient, we examine how indicative the minimal seed – the disturbance of smallest energy for transition – is in measuring transition thresholds. We first show that the minimal seed is relatively robust to base profile changes and spectral filtering. We then compare the (unforced) transition behaviour of the minimal seed with several forms of randomised initial conditions in the range of Reynolds numbers 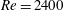$Re=2400$–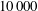$10\,000$ and find that the energy of the minimal seed after the Orr and oblique phases of its evolution is close to that of a critical localised random disturbance. In this sense, the minimal seed at the end of the oblique phase can be regarded as a good proxy for typical disturbances (here taken to be the localised random ones) and is thus used as initial condition in the simulations with the body force. The enhanced nonlinear stability and drag reduction predicted in the present study are an encouraging first step in modelling the experiments of Kühnen et al. and should motivate future developments to fully exploit the benefits of this promising direction for flow control.

JFM classification

Instability: Transition to turbulence
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 863 , 25 March 2019 , pp. 850 - 875
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Auteri, F., Baron, A., Belan, M., Campanardi, G. & Quadrio, M. 2010 Experimental assessment of drag reduction by traveling waves in a turbulent pipe flow. Phys. Fluids 22 (11), 115103.10.1063/1.3491203Google Scholar
Avila, K., Moxey, D., de Lozar, A., Avila, M., Barkley, D. & Hof, B. 2011 The onset of turbulence in pipe flow. Science 333, 192–196.10.1126/science.1203223Google Scholar
Bewley, T. R. 2001 Flow control: new challenges for a new renaissance. Prog. Aerosp. Sci. 37 (1), 21–58.10.1016/S0376-0421(00)00016-6Google Scholar
Blasius, H. 1913 Das ähnlichkeitsgesetz bei reibungsvorgängen in flüssigkeiten. In Mitteilungen über Forschungsarbeiten auf dem Gebiete des Ingenieurwesens, pp. 1–41. Springer.Google Scholar
Brandt, L. 2014 The lift-up effect: the linear mechanism behind transition and turbulence in shear flows. Eur. J. Mech. (B/Fluids) 47, 80–96.10.1016/j.euromechflu.2014.03.005Google Scholar
Cherubini, S., De Palma, P. & Robinet, J.-Ch. 2015 Nonlinear optimals in the asymptotic suction boundary layer: transition thresholds and symmetry breaking. Phys. Fluids 27 (3), 034108.10.1063/1.4916017Google Scholar
Cherubini, S., De Palma, P., Robinet, J.-Ch. & Bottaro, A. 2012 A purely nonlinear route to transition approaching the edge of chaos in a boundary layer. Fluid Dyn. Res. 44 (3), 031404.10.1088/0169-5983/44/3/031404Google Scholar
Cherubini, S. & Palma, P. D. 2014 Minimal perturbations approaching the edge of chaos in a couette flow. Fluid Dyn. Res. 46 (4), 041403.10.1088/0169-5983/46/4/041403Google Scholar
Choi, H., Moin, P. & Kim, J. 1994 Active turbulence control for drag reduction in wall-bounded flows. J. Fluid Mech. 262, 75–110.10.1017/S0022112094000431Google Scholar
Choi, J.-I., Xu, C.-X. & Sung, H. J. 2002 Drag reduction by spanwise wall oscillation in wall-bounded turbulent flows. AIAA 40 (5), 842–850.10.2514/2.1750Google Scholar
Choi, K.-S. & Graham, M. 1998 Drag reduction of turbulent pipe flows by circular-wall oscillation. Phys. Fluids 10 (1), 7–9.10.1063/1.869538Google Scholar
Darbyshire, A. G. & Mullin, T. 1995 Transition to turbulence in constant-mass-flux pipe flow. J. Fluid Mech. 289, 83–114.10.1017/S0022112095001248Google Scholar
Duggleby, A., Ball, K. S. & Paul, M. R. 2007 The effect of spanwise wall oscillation on turbulent pipe flow structures resulting in drag reduction. Phys. Fluids 19 (12), 125107.10.1063/1.2825428Google Scholar
Duguet, Y., Monokrousos, A., Brandt, L. & Henningson, D. S. 2013 Minimal transition thresholds in plane Couette flow. Phys. Fluids 25 (8), 084103.10.1063/1.4817328Google Scholar
Eckhardt, B., Schneider, T. M., Hof, B. & Westerweel, J. 2007 Turbulence transition in pipe flow. Annu. Rev. Fluid Mech. 29, 447–468.10.1146/annurev.fluid.39.050905.110308Google Scholar
Fadlun, E. A., Verzicco, R., Orlandi, P. & Mohd-Yusof, J. 2000 Combined immersed-boundary finite-difference methods for three-dimensional complex flow simulations. J. Comput. Phys. 161 (1), 35–60.10.1006/jcph.2000.6484Google Scholar
He, S., He, K. & Seddighi, M. 2016 Laminarisation of flow at low Reynolds number due to streamwise body force. J. Fluid Mech. 809, 31–71.10.1017/jfm.2016.653Google Scholar
Hof, B., De Lozar, A., Avila, M., Tu, X. & Schneider, T. M. 2010 Eliminating turbulence in spatially intermittent flows. Science 327 (5972), 1491–1494.10.1126/science.1186091Google Scholar
Hof, B., Juel, A. & Mullin, T. 2003 Scaling of the turbulence transition threshold in a pipe. Phys. Rev. Lett. 91, 244502.10.1103/PhysRevLett.91.244502Google Scholar
Högberg, M., Bewley, T. R. & Henningson, D. S. 2003 Linear feedback control and estimation of transition in plane channel flow. J. Fluid Mech. 481, 149–175.10.1017/S0022112003003823Google Scholar
Jovanović, M. R. 2008 Turbulence suppression in channel flows by small amplitude transverse wall oscillations. Phys. Fluids 20 (1), 014101.10.1063/1.2824401Google Scholar
Kasagi, N., Suzuki, Y. & Fukagata, K. 2009 Microelectromechanical systems-based feedback control of turbulence for skin friction reduction. Annu. Rev. Fluid Mech. 41, 231–251.10.1146/annurev.fluid.010908.165221Google Scholar
Kerswell, R. R. 2005 Recent progress in understanding the transition to turbulence in a pipe. Nonlinearity 18, R17–R44.10.1088/0951-7715/18/6/R01Google Scholar
Kerswell, R. R. 2018 Nonlinear nonmodal stability theory. Annu. Rev. Fluid Mech. 50 (1), 319–345.10.1146/annurev-fluid-122316-045042Google Scholar
Kerswell, R. R., Pringle, C. C. T. & Willis, A. P. 2014 An optimization approach for analysing nonlinear stability with transition to turbulence in fluids as an exemplar. Rep. Prog. Phys. 77 (8), 085901.10.1088/0034-4885/77/8/085901Google Scholar
Kim, J. & Bewley, T. R. 2007 A linear systems approach to flow control. Annu. Rev. Fluid Mech. 39, 383–417.10.1146/annurev.fluid.39.050905.110153Google Scholar
Kim, J., Moin, P. & Moser, R. 1987 Turbulence statistics in fully developed channel flow at low Reynolds number. J. Fluid Mech. 177, 133–166.10.1017/S0022112087000892Google Scholar
Kühnen, J., Scarselli, D., Schaner, M. & Hof, B. 2018a Relaminarization by steady modification of the streamwise velocity profile in a pipe. Flow Turbul. Combust. 100 (4), 919–943.10.1007/s10494-018-9896-4Google Scholar
Kühnen, J., Song, B., Scarselli, D., Budanur, N. B., Riedl, M., Willis, A., Avila, M. & Hof, B. 2018b Destabilizing turbulence in pipe flow. Nat. Phys. 14 (4), 386–390.10.1038/s41567-017-0018-3Google Scholar
Lee, C., Kim, J. & Choi, H. 1998 Suboptimal control of turbulent channel flow for drag reduction. J. Fluid Mech. 358, 245–258.10.1017/S002211209700815XGoogle Scholar
Lumley, J. & Blossey, P. 1998 Control of turbulence. Annu. Rev. Fluid Mech. 30 (1), 311–327.10.1146/annurev.fluid.30.1.311Google Scholar
Mellibovsky, F. & Meseguer, A. 2009 Critical threshold in pipe flow transition. Phil. Trans. R. Soc. Lond. A 367 (1888), 545–560.10.1098/rsta.2008.0165Google Scholar
Moarref, R. & Jovanović, M. R. 2010 Controlling the onset of turbulence by streamwise travelling waves. Part 1. Receptivity analysis. J. Fluid Mech. 663, 70–99.10.1017/S0022112010003393Google Scholar
Mullin, T. 2011 Experimental studies of transition to turbulence in a pipe. Annu. Rev. Fluid Mech. 43, 1–24.10.1146/annurev-fluid-122109-160652Google Scholar
Peixinho, J. & Mullin, T. 2007 Finite-amplitude thresholds for transition in pipe flow. J. Fluid Mech. 582, 169–178.10.1017/S0022112007006398Google Scholar
Pfenninger, W. 1961 Transition in the inlet length of tubes at high Reynolds numbers. In Boundary Layer and Flow Control (ed. Lachmann, G. V.), pp. 970–980. Pergamon.Google Scholar
Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.10.1017/CBO9780511840531Google Scholar
Pringle, C. C. T. & Kerswell, R. R. 2010 Using nonlinear transient growth to construct the minimal seed for shear flow turbulence. Phys. Rev. Lett. 105, 154502.10.1103/PhysRevLett.105.154502Google Scholar
Pringle, C. C. T., Willis, A. P. & Kerswell, R. R. 2012 Minimal seeds for shear flow turbulence: using nonlinear transient growth to touch the edge of chaos. J. Fluid Mech. 702, 415–443.10.1017/jfm.2012.192Google Scholar
Quadrio, M. 2011 Drag reduction in turbulent boundary layers by in-plane wall motion. Phil. Trans. R. Soc. Lond. A 369 (1940), 1428–1442.10.1098/rsta.2010.0366Google Scholar
Quadrio, M. & Sibilla, S. 2000 Numerical simulation of turbulent flow in a pipe oscillating around its axis. J. Fluid Mech. 424, 217–241.10.1017/S0022112000001889Google Scholar
Rabin, S. M. E., Caulfield, C. P. & Kerswell, R. R. 2014 Designing a more nonlinearly stable laminar flow via boundary manipulation. J. Fluid Mech. 738, 1–12.10.1017/jfm.2013.601Google Scholar
Reddy, S. C., Schmid, P. J., Baggett, J. S. & Henningson, D. S. 1998 On stability of streamwise streaks and transition thresholds in plane channel flows. J. Fluid Mech. 365, 269–303.10.1017/S0022112098001323Google Scholar
Reynolds, O. 1883 An experimental investigation of the circumstances which determine whether the motion of water shall be direct or sinuous, and the law of resistance in parallel channels. Proc. R. Soc. Lond. A 174, 935–982.Google Scholar
Schmid, P. J. & Henningson, D. S. 2012 Stability and Transition in Shear Flows, vol. 142. Springer Science & Business Media.Google Scholar
Schneider, T. M. & Eckhardt, B. 2008 Lifetime statistics in transitional pipe flow. Phys. Rev. E 78 (4), 046310.Google Scholar
Schoppa, W. & Hussain, F. 2002 Coherent structure generation in near-wall turbulence. J. Fluid Mech. 453, 57–108.10.1017/S002211200100667XGoogle Scholar
Trefethen, L. N., Chapman, S. J., Henningson, D. S., Meseguer, A., Mullin, T. & Nieuwstadt, F. T.2000 Threshold amplitudes for transition to turbulence in a pipe. Numer. Anal. Rep. 00/17. Oxford University Computer Laboratory.Google Scholar
Waleffe, F. 1997 On a Self-Sustaining Process in shear flows. Phys. Fluids 9, 883–900.10.1063/1.869185Google Scholar
Willis, A. P. 2017 The Openpipeflow Navier–Stokes solver. SoftwareX 6, 124–127.10.1016/j.softx.2017.05.003Google Scholar
Willis, A. P., Hwang, Y. & Cossu, C. 2010 Optimally amplified large-scale streaks and drag reduction in turbulent pipe flow. Phys. Rev. E 82, 036321.Google Scholar
Willis, A. P., Peixinho, J., Kerswell, R. R. & Mullin, T. 2008 Experimental and theoretical progress in pipe flow transition. Phil. Trans. R. Soc. Lond. A 366, 2671–2684.10.1098/rsta.2008.0063Google Scholar
Wygnanski, I. J. & Champagne, F. H. 1973 On transition in a pipe. Part 1. The origin of puffs and slugs and the flow in a turbulent slug. J. Fluid Mech. 59, 281–335.10.1017/S0022112073001576Google Scholar
Xu, C.-X., Choi, J.-I. & Sung, H. J. 2002 Suboptimal control for drag reduction in turbulent pipe flow. Fluid Dyn. Res. 30 (4), 217–231.10.1016/S0169-5983(02)00041-2Google Scholar
Yudhistira, I. & Skote, M. 2011 Direct numerical simulation of a turbulent boundary layer over an oscillating wall. J. Turbul. 12, N9.10.1080/14685248.2010.538397Google Scholar
Zhou, D. & Ball, K. S. 2008 Turbulent drag reduction by spanwise wall oscillations. Int. J. Eng. Trans. 21 (1), 85.Google Scholar