Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-26T16:29:54.777Z Has data issue: false hasContentIssue false
  • English
  • Français

Squirmer locomotion in a yield stress fluid

Published online by Cambridge University Press:  16 September 2022

Patrick S. Eastham Open the ORCID record for Patrick S. Eastham [Opens in a new window] ,
Hadi Mohammadigoushki Open the ORCID record for Hadi Mohammadigoushki [Opens in a new window]  and
Kourosh Shoele Open the ORCID record for Kourosh Shoele [Opens in a new window]
Patrick S. Eastham
Affiliation:
Department of Psychology, Florida State University, Tallahassee, FL 32311, USA
Hadi Mohammadigoushki
Affiliation:
Department of Chemical and Biomedical Engineering, FAMU-FSU College of Engineering, Tallahassee, FL 32310, USA
Kourosh Shoele*
Affiliation:
Department of Mechanical Engineering, FAMU-FSU College of Engineering, Tallahassee, FL32310, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

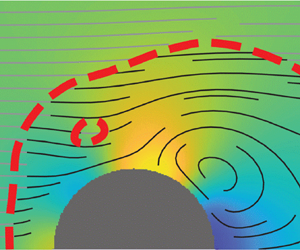
An axisymmetric squirmer in a Bingham viscoplastic fluid is studied numerically to determine the effect of a yield stress environment on locomotion. The nonlinearity of the governing equations necessitates numerical methods, which are accomplished by solving a variable-viscosity Stokes equation with a finite element approach. The effects of stroke modes, both pure and combined, are investigated, and it is found that for the treadmill or ‘neutral’ mode, the swimmer in a yield stress fluid has a lower swimming velocity and uses more power. However, the efficiency of swimming reaches its maximum at a finite yield limit. In addition, for higher yield limits, higher stroke modes can increase the swimming velocity and hydrodynamic efficiency of the treadmill swimmer. The higher-order odd-numbered squirming modes, particularly the third stroke mode, can generate propulsion by themselves that increases in strength as the viscoplastic nonlinearity increases to a specific limit. These results are closely correlated with the confinement effects induced by the viscoplastic rigid surface surrounding the swimming body, showing that swimmers in viscoplastic environments, both biological and artificial, could potentially employ other non-standard swimming strategies to optimize their locomotion.

JFM classification

Biological Fluid Dynamics: Micro-organism dynamics Non-Newtonian Flows: Plastic materials
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 948 , 10 October 2022 , A54
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Bansil, R., Celli, J., Hardcastle, J. & Turner, B. 2013 The influence of mucus microstructure and rheology in helicobacter pylori infection. Front. Immunol. 4, 310.CrossRefGoogle ScholarPubMed
Binagia, J.P., Phoa, A., Housiadas, K.D. & Shaqfeh, E.S.G. 2020 Swimming with swirl in a viscoelastic fluid. J. Fluid Mech. 900, A4.CrossRefGoogle Scholar
Blake, J.R. 1971 A spherical envelope approach to ciliary propulsion. J. Fluid Mech. 46 (1), 199–208.CrossRefGoogle Scholar
Bunea, A.-I. & Taboryski, R. 2020 Recent advances in microswimmers for biomedical applications. Micromachines 11 (12), 1048.CrossRefGoogle ScholarPubMed
Curt, J.R.N. & Pringle, R. 1969 Viscosity of gastric mucus in duodenal ulceration. Gut 10 (11), 931–934.CrossRefGoogle ScholarPubMed
Datt, C., Natale, G., Hatzikiriakos, S.G. & Elfring, G.J. 2017 An active particle in a complex fluid. J. Fluid Mech. 823, 675–688.CrossRefGoogle Scholar
Datt, C., Zhu, L., Elfring, G.J. & Pak, O.S. 2015 Squirming through shear-thinning fluids. J. Fluid Mech. 784, R1.CrossRefGoogle Scholar
Eastham, P.S. 2019 eFEMpart. https://github.com/pseastham/eFEMpart.Google Scholar
Eastham, P.S. & Shoele, K. 2020 Axisymmetric squirmers in Stokes fluid with nonuniform viscosity. Phys. Rev. Fluids 5 (6), 063102.CrossRefGoogle Scholar
Elfring, G.J. & Lauga, E. 2015 Theory of locomotion through complex fluids. In Complex Fluids in Biological Systems, pp. 283–317. Springer.CrossRefGoogle Scholar
van Gogh, B., Demir, E., Palaniappan, D. & Pak, O.S. 2022 The effect of particle geometry on squirming through a shear-thinning fluid. J. Fluid Mech. 938, A3.CrossRefGoogle Scholar
Hewitt, D.R. & Balmforth, N.J. 2017 Taylor's swimming sheet in a yield-stress fluid. J. Fluid Mech. 828, 33–56.CrossRefGoogle Scholar
Hewitt, D.R. & Balmforth, N.J. 2018 Viscoplastic slender-body theory. J. Fluid Mech. 856, 870–897.CrossRefGoogle Scholar
Hewitt, D.R. & Balmforth, N.J. 2022 Locomotion with a wavy cylindrical filament in a yield-stress fluid. J. Fluid Mech. 936, A17.CrossRefGoogle Scholar
Lauga, E. 2009 Life at high Deborah number. Europhys. Lett. 86 (6), 64001.CrossRefGoogle Scholar
Lauga, E. 2016 Bacterial hydrodynamics. Annu. Rev. Fluid Mech. 48, 105–130.CrossRefGoogle Scholar
Li, G., Lauga, E. & Ardekani, A.M. 2021 Microswimming in viscoelastic fluids. J. Non-Newtonian Fluid Mech. 297, 104655.CrossRefGoogle Scholar
Li, G.-J., Karimi, A. & Ardekani, A.M. 2014 Effect of solid boundaries on swimming dynamics of microorganisms in a viscoelastic fluid. Rheol. Acta 53 (12), 911–926.CrossRefGoogle Scholar
Lighthill, M.J. 1952 On the squirming motion of nearly spherical deformable bodies through liquids at very small Reynolds numbers. Commun. Pure Appl. Maths 5 (2), 109–118.CrossRefGoogle Scholar
Lighthill, S.J. 1975 Mathematical Biofluiddynamics. SIAM.CrossRefGoogle Scholar
Michelin, S. & Lauga, E. 2010 Efficiency optimization and symmetry-breaking in a model of ciliary locomotion. Phys. Fluids 22 (11), 111901.CrossRefGoogle Scholar
Michelin, S. & Lauga, E. 2011 Optimal feeding is optimal swimming for all Péclet numbers. Phys. Fluids 23 (10), 101901.CrossRefGoogle Scholar
Mirbagheri, S.A. & Fu, H.C. 2016 Helicobacter pylori couples motility and diffusion to actively create a heterogeneous complex medium in gastric mucus. Phys. Rev. Lett. 116 (19), 198101.CrossRefGoogle ScholarPubMed
Nganguia, H. & Pak, O.S. 2018 Squirming motion in a Brinkman medium. J. Fluid Mech. 855, 554–573.CrossRefGoogle Scholar
Nganguia, H., Pietrzyk, K. & Pak, O.S. 2017 Swimming efficiency in a shear-thinning fluid. Phys. Rev. E 96 (6), 062606.CrossRefGoogle Scholar
Nganguia, H., Zhu, L., Palaniappan, D. & Pak, O.S. 2020 Squirming in a viscous fluid enclosed by a Brinkman medium. Phys. Rev. E 101 (6), 063105.CrossRefGoogle Scholar
Pedley, T.J. 2016 Spherical squirmers: models for swimming micro-organisms. IMA J. Appl. Maths 81 (3), 488–521.CrossRefGoogle Scholar
Pietrzyk, K., Nganguia, H., Datt, C., Zhu, L., Elfring, G.J. & Pak, O.S. 2019 Flow around a squirmer in a shear-thinning fluid. J. Non-Newtonian Fluid Mech. 268, 101–110.CrossRefGoogle Scholar
Reigh, S.Y. & Lauga, E. 2017 Two-fluid model for locomotion under self-confinement. Phys. Rev. Fluids 2 (9), 093101.CrossRefGoogle Scholar
Saramito, P. 2016 Complex Fluids. Springer.CrossRefGoogle Scholar
Saramito, P. & Wachs, A. 2017 Progress in numerical simulation of yield stress fluid flows. Rheol. Acta 56 (3), 211–230.CrossRefGoogle Scholar
Stone, H.A. & Samuel, A.D.T. 1996 Propulsion of microorganisms by surface distortions. Phys. Rev. Lett. 77 (19), 4102.CrossRefGoogle ScholarPubMed
Supekar, R., Hewitt, D.R. & Balmforth, N.J. 2020 Translating and squirming cylinders in a viscoplastic fluid. J. Fluid Mech. 882, A11.CrossRefGoogle Scholar
Tam, D. & Hosoi, A.E. 2007 Optimal stroke patterns for Purcell's three-link swimmer. Phys. Rev. Lett. 98 (6), 068105.CrossRefGoogle ScholarPubMed
Tsang, A.C.H., Demir, E., Ding, Y. & Pak, O.S. 2020 Roads to smart artificial microswimmers. Adv. Intell. Syst. 2 (8), 1900137.CrossRefGoogle Scholar
Wu, S., Solano, T., Shoele, K. & Mohammadigoushki, H. 2022 Formation of a strong negative wake behind a helical swimmer in a viscoelastic fluid. J. Fluid Mech. 942, A10.CrossRefGoogle Scholar
Wu, Z., Chen, Y., Mukasa, D., Pak, O.S. & Gao, W. 2020 Medical micro/nanorobots in complex media. Chem. Soc. Rev. 49 (22), 8088–8112.CrossRefGoogle ScholarPubMed
Zhu, L., Lauga, E. & Brandt, L. 2012 Self-propulsion in viscoelastic fluids: pushers vs pullers. Phys. Fluids 24 (5), 051902.CrossRefGoogle Scholar