Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-27T00:36:37.377Z Has data issue: false hasContentIssue false
  • English
  • Français

Spray dispersion regimes following atomization in a turbulent co-axial gas jet

Published online by Cambridge University Press:  09 December 2021

P.D. Huck Open the ORCID record for P.D. Huck [Opens in a new window] ,
R. Osuna-Orozco ,
N. Machicoane Open the ORCID record for N. Machicoane [Opens in a new window]  and
A. Aliseda Open the ORCID record for A. Aliseda [Opens in a new window]
P.D. Huck
Affiliation:
Department of Mechanical Engineering, University of Washington, Seattle, WA, 98195, USA
R. Osuna-Orozco
Affiliation:
Department of Mechanical Engineering, University of Washington, Seattle, WA, 98195, USA
N. Machicoane
Affiliation:
Department of Mechanical Engineering, University of Washington, Seattle, WA, 98195, USA University of Grenoble Alpes, CNRS, Grenoble INP, LEGI, 38000 Grenoble, France
A. Aliseda*
Affiliation:
Department of Mechanical Engineering, University of Washington, Seattle, WA, 98195, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

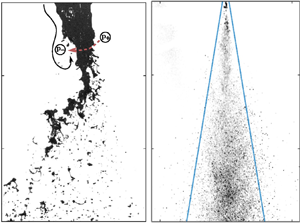
A canonical co-axial round-jet two-fluid atomizer where atomization occurs over a wide range of momentum ratios: $M=1.9 - 376.4$ is studied. The near field of the spray, where the droplet formation process takes place, is characterized and linked to droplet dispersion in the far field of the jet. Counterintuitively, our results indicate that in the low-momentum regime, increasing the momentum in the gas phase leads to less droplet dispersion. A critical momentum ratio of the order of $M_c=50$, that separates this regime from a high-momentum one with less dispersion, is found in both the near and far fields. A phenomenological model is proposed that determines the susceptibility of droplets to disperse beyond the nominal extent of the gas phase based on a critical Stokes number, $St=\tau _p/T_E=1.9$, formulated based on the local Eulerian large scale eddy turnover time, $T_E$, and the droplets’ response time, $\tau _p$. A two-dimensional phase space summarizes the extent of these different regimes in the context of spray characteristics found in the literature.

JFM classification

Multiphase and Particle-laden Flows: Multiphase flow Multiphase and Particle-laden Flows: Particle/fluid flow Drops and Bubbles: Aerosols/atomization
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 932 , 10 February 2022 , A36
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Abkarian, M., Mendez, S., Xue, N., Yang, F. & Stone, H.A. 2020 Speech can produce jet-like transport relevant to asymptomatic spreading of virus. Proc. Natl Acad. Sci. USA 117 (41), 25237–25245.CrossRefGoogle ScholarPubMed
Albrecht, H.E., Borys, M., Damaschke, E. & Tropea, C. 2003 Laser Doppler and Phase Doppler Measurement Techniques. Springer.CrossRefGoogle Scholar
Bachalo, W.D. 1994 Experimental methods in multiphase flows. Intl J. Multiphase Flow 20 (SUPPL. 1), 261–295.CrossRefGoogle Scholar
Balachandar, S., Zaleski, S., Soldati, A., Ahmadi, G. & Bourouiba, L. 2020 Host-to-host airborne transmission as a multiphase flow problem for science-based social distance guidelines. Intl J. Multiphase Flow 132, 103439.CrossRefGoogle Scholar
Brown, G.L. & Roshko, A. 1974 On density effects and large structure in turbulent mixing layers. J. Fluid Mech. 64 (4), 775–816.CrossRefGoogle Scholar
Chung, J.N. & Troutt, T.R. 1988 Simulation of particle dispersion in an axisymmetric jet. J. Fluid Mech. 186, 199–222.CrossRefGoogle Scholar
Delon, A., Cartellier, A. & Matas, J.-P. 2018 Flapping instability of a liquid jet. Phys. Rev. Fluids 3 (4), 043901.CrossRefGoogle Scholar
Dimotakis, P.E. 1986 Two-dimensional shear-layer entrainment. AIAA 24 (11), 1791–1796.CrossRefGoogle Scholar
Dimotakis, P.E., Miake-Lye, R.C. & Papantoniou, D.A. 1983 Structure and dynamics of round turbulent jets. Phys. Fluids 26 (11), 3185–3192.CrossRefGoogle Scholar
Dumouchel, C. 2008 On the experimental investigation on primary atomization of liquid streams. Exp. Fluids 45 (3), 371–422.CrossRefGoogle Scholar
Eaton, J.K. & Johnston, J.P. 1980 Review of research on subsonic turbulent-flow reattachment. AIAA Paper 19 (9), 1093–1100.Google Scholar
Eaton, J.K. & Johnston, J.P. 1982 Low frequency unsteadyness of a reattaching turbulent shear layer. Turbul. Shear Flows 3, 162–170.CrossRefGoogle Scholar
Engelbert, C., Hardalupas, Y. & Whitelaw, J.H. 1995 Breakup phenomena in coaxial airblast atomizers. Proc. R. Soc. Lond. A 451, 189–229.Google Scholar
Eroglu, H. & Chigier, N. 1991 Initial drop size and velocity distributions for airblast coaxial atomizers. Trans. ASME J. Fluids Engng 113 (3), 453–459.CrossRefGoogle Scholar
Favre-Marinet, M., Camano, E.B. & Sarboch, J. 1999 Near-field of coaxial jets with large density differences. Exp. Fluids 26 (1–2), 97–106.CrossRefGoogle Scholar
Hardalupas, Y, Taylor, A.M.K.P. & Whitelaw, J.H. 1989 Velocity and particle-flux characteristics of turbulent particle-laden jets. Proc. R. Soc. Lond. A 78 (1870), 185–195.Google Scholar
Hardalupas, Y, Taylor, A.M.K.P. & Whitelaw, J.H. 1990 Velocity and size characteristics of liquid-fuelled flames stabilized by a swirl burner. Proc. R. Soc. Lond. A 428 (1874), 129–155.Google Scholar
Hardalupas, Y & Whitelaw, J.H.W. 1993 Coaxial Airblast Atomizers. Tech. Rep. Imperial College of Science and Technology.Google Scholar
Hardalupas, Y.H. & Whitelaw, J.H.W. 1994 Characteristics of sprays produced by coaxial airblast atomizers. J. Propul. Power 10 (4), 453–460.CrossRefGoogle Scholar
Kumar, A. & Sahu, S. 2020 Liquid jet disintegration memory effect on downstream spray fluctuations in a coaxial twin-fluid injector. Phys. Fluids 32 (7), 073302.CrossRefGoogle Scholar
Lampa, A. & Fritsching, U. 2013 Large eddy simulation of the spray formation in confinements. Intl J. Heat Fluid Flow 43, 26–34.CrossRefGoogle Scholar
Lasheras, J.C. & Hopfinger, E.J. 2000 Liquid jet instability nd atomization in a coaxial gas strea. Annu. Rev. Fluid Mech. 1 (1873), 406–459.Google Scholar
Lasheras, J.C., Villermaux, E. & Hopfinger, E.J. 1998 Break-up and atomization of a round water jet by a high-speed annular air jet. J. Fluid Mech. 357, 351–379.CrossRefGoogle Scholar
Lau, T.C.W. & Nathan, G.J. 2014 Influence of Stokes number on the velocity and concentration distributions in particle-laden jets. J. Fluid Mech. 757 (6), 432–457.CrossRefGoogle Scholar
Lau, T.C.W. & Nathan, G.J. 2016 The effect of Stokes number on particle velocity and concentration distributions in a well-characterised, turbulent, co-flowing two-phase jet. J. Fluid Mech. 809, 72–110.CrossRefGoogle Scholar
Lazaro, B.J. & Lasheras, J.C. 1992 a Particle dispersion in the developing free shear layer. Part 1. Unforced flow. J. Fluid Mech. 235, 143–178.Google Scholar
Lazaro, B.J. & Lasheras, J.C. 1992 b Particle dispersion in the developing free shear layer. Part 2. Forced flow. J. Fluid Mech. 235, 179–221.Google Scholar
Ling, Y., Fuster, D., Tryggvason, G. & Zaleski, S. 2019 A two-phase mixing layer between parallel gas and liquid streams: multiphase turbulence statistics and influence of interfacial instability. J. Fluid Mech. 859, 268–307.CrossRefGoogle Scholar
Longmire, E.K. & Eaton, J.K. 1992 Structure of a particle-laden round jet. 236.CrossRefGoogle Scholar
Lozano, A. & Barreras, F. 2001 Experimental study of the gas flow in an air-blasted liquid sheet. Exp. Fluids 31 (4), 367–376.CrossRefGoogle Scholar
Machicoane, N., Bothell, J.K., Li, D., Morgan, T.B., Heindel, T.J., Kastengren, A.L. & Aliseda, A. 2019 Synchrotron radiography characterization of the liquid core dynamics in a canonical two-fluid coaxial atomizer. Intl J. Multiphase Flow 115, 1–8.CrossRefGoogle Scholar
Machicoane, N., Ricard, G., Osuna-Orozco, R., Huck, P.D. & Aliseda, A. 2020 Influence of steady and oscillating swirl on the near-field spray characteristics in a two-fluid coaxial atomizer. Intl J. Multiphase Flow 129, 103318.CrossRefGoogle Scholar
Marmottant, P.H. & Villermaux, E. 2004 On spray formation. J. Fluid Mech. 498 (498), 73–111.CrossRefGoogle Scholar
Matas, J.-P., Delon, A.A. & Cartellier, A. 2018 Shear instability of an axisymmetric air-water coaxial jet. J. Fluid Mech. 843, 575–600.CrossRefGoogle Scholar
Modarress, D., Wuerer, J. & Elghobashi, S. 1984 An experimental study of a turbulent round two-phase jet. Chem. Engng Commun. 28 (4–6), 341–354.CrossRefGoogle Scholar
Mungal, M.G. & Hollingsworth, D.K. 1989 Organized motion in a very high Reynolds number jet. Phys. Fluids A 1 (10), 1615–1624.CrossRefGoogle Scholar
Osuna-Orozco, R., Machicoane, N., Huck, P.D. & Aliseda, A. 2019 Feedback control of coaxial atomization based on the spray liquid distribution. At. Sprays 29 (6), 545–551.CrossRefGoogle Scholar
Osuna-Orozco, R., Machicoane, N., Huck, P.D. & Aliseda, A. 2020 Feedback control of the spray liquid distriubtion of electrostatically assisted coaxial atomization. At. Sprays 30 (1), 1–9.CrossRefGoogle Scholar
Panchapakesan, N.R. & Lumley, J.L. 1993 Turbulence measurements in axisymmetric jets of air and helium. Part 1. Air jet. J. Fluid Mech. 246, 225–247.CrossRefGoogle Scholar
Picano, F., Sardina, G., Gualtieri, P. & Casciola, C.M. 2010 Anomalous memory effects on transport of inertial particles in turbulent jets. Phys. Fluids 22 (5), 051705.CrossRefGoogle Scholar
Pope, S.B. 2010 Turbulent Flows. Cambridge University Press.Google Scholar
Prevost, F, Boree, J., Nuglisch, H.J. & Charnay, G. 1996 Measurements of fluid/particle correlated motion in the far field of an axisymmetric jet. Intl J. Multiphase Flow 22 (4), 685–701.CrossRefGoogle Scholar
Reeks, M.W. 1983 The transport of discrete particles in inhomogeneous turbulence. J. Aerosol Sci. 14 (6), 729–739.CrossRefGoogle Scholar
Rehab, H., Villermaux, E. & Hopfinger, E.J. 1997 Flow regimes of large-velocity-ratio coaxial jets. J. Fluid Mech. 345, 357–381.CrossRefGoogle Scholar
Saffman, P.G. 1965 The lift on a small sphere in a slow shear flow. J. Fluid Mech. 22, 385–400.CrossRefGoogle Scholar
Sbrizzai, F., Verzicco, R., Pidria, M.F. & Soldati, A. 2004 Mechanisms for selective radial dispersion of microparticles in the transitional region of a confined turbulent round jet. Intl J. Multiphase Flow 30 (11), 1389–1417.CrossRefGoogle Scholar
Tso, J. & Hussain, F. 1989 Organized motions in a fully developed turbulent axisymmetric jet. J. Fluid Mech. 203 (425), 425–448.CrossRefGoogle Scholar
Ünal, A. 1989 Understanding liquid-jet atomization cascades via vortex dynamics. Metall. Mater. Trans. B 20B, 61–69.CrossRefGoogle Scholar
Villermaux, E., Marmottant, P. & Duplat, J. 2004 Ligament-mediated spray formation. Phys. Rev. Lett. 92 (7), 074501.CrossRefGoogle ScholarPubMed
Wygnanski, I. & Fiedler, H. 1969 Some measurements in the self-preserving jet. J. Fluid Mech. 38 (3), 577–612.CrossRefGoogle Scholar
Yoda, M., Hesselink, L. & Mungal, M.G. 1992 The evolution and nature of large-scale structures in the turbulent jet. Phys. Fluids A 4 (4), 803–811.CrossRefGoogle Scholar
Yule, A.J. 1978 Large-scale structure in the mixing layer of a round jet. J. Fluid Mech. 89 (3), 413–432.CrossRefGoogle Scholar
Zaller, M.M. & Klem, M.D. 1991 Coaxial Injector Spray Characterization Using Water/Air as Simulants. NASA Tech. Rep. 105322.Google Scholar
Zaller, M.M. & Klem, M.D. 1995 Shear coaxial injector spray characterization. In Liquid Rocket Engine Combustion Instability (ed. V. Yang & W. Anderson), chap. 7, pp. 191–192. American Institute of Aeronautics and Astronautics, Inc.Google Scholar
Zandian, A., Sirignano, W.A. & Hussain, F. 2018 Understanding liquid-jet atomization cascades via vortex dynamics. J. Fluid Mech. 843, 293–354.CrossRefGoogle Scholar