Hostname: page-component-745bb68f8f-lrblm Total loading time: 0 Render date: 2025-01-08T10:21:37.771Z Has data issue: false hasContentIssue false
  • English
  • Français

Split energy–helicity cascades in three-dimensional homogeneous and isotropic turbulence

Published online by Cambridge University Press:  30 July 2013

L. Biferale ,
S. Musacchio  and
F. Toschi
L. Biferale*
Affiliation:
Department of Physics and INFN, University of Rome Tor Vergata, Via della Ricerca Scientifica 1, 00133 Rome, Italy
S. Musacchio
Affiliation:
CNRS, Laboratoire J. A. Dieudonné UMR 6621, Parc Valrose, 06108 Nice, France
F. Toschi
Affiliation:
Department of Physics and Department of Mathematics and Computer Science, Eindhoven University of Technology, 5600 MB Eindhoven, The Netherlands CNR-IAC, Via dei Taurini 19, 00185 Rome, Italy
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We investigate the transfer properties of energy and helicity fluctuations in fully developed homogeneous and isotropic turbulence by changing the nature of the nonlinear Navier–Stokes terms. We perform a surgery of all possible interactions, by keeping only those triads that have sign-definite helicity content. In order to do this, we apply an exact decomposition of the velocity field in a helical Fourier basis, as first proposed by Constantin & Majda (Commun. Math. Phys, vol. 115, 1988, p. 435) and exploited in great detail by Waleffe (Phys. Fluids A, vol. 4, 1992, p. 350), and we evolve the Navier–Stokes dynamics keeping only those velocity components carrying a well-defined (positive or negative) helicity. The resulting dynamics preserves translational and rotational symmetries but not mirror invariance. 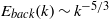We give clear evidence that this three-dimensional homogeneous and isotropic chiral turbulence is characterized by a stationary inverse energy cascade with a spectrum ${E}_{back} (k)\sim {k}^{- 5/ 3} $ and by a direct helicity cascade with a spectrum 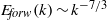${E}_{forw} (k)\sim {k}^{- 7/ 3} $. Our results are important to highlight the dynamics and statistics of those subsets of all possible Navier–Stokes interactions responsible for reversal events in the energy-flux properties, and demonstrate that the presence of an inverse energy cascade is not necessarily connected to a two-dimensionalization of the flow. We further comment on the possible relevance of such findings to flows of geophysical interest under rotations and in thin layers. Finally we propose other innovative numerical experiments that can be achieved by using a similar decimation of degrees of freedom.

JFM classification

Turbulent Flows: Isotropic turbulence Turbulent Flows: Turbulence theory
Type
Papers
Information
Journal of Fluid Mechanics , Volume 730 , 10 September 2013 , pp. 309 - 327
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

André, J. C. & Lesieur, M. 1977 Influence of helicity on the evolution of isotropic turbulence at high Reynolds number. J. Fluid Mech. 81, 187–207.CrossRefGoogle Scholar
Baggaley, A. W., Barenghi, C. F. & Sergeev, Y. A. 2012 Three-dimensional inverse energy cascade induced by vortex reconnections. arXiv:1208.5204.Google Scholar
Benzi, R., Biferale, L., Kerr, R. & Trovatore, E. 1996 Helical shell models for three-dimensional turbulence. Phys. Rev. E 53, 3541–3550.Google Scholar
Benzi, R., Biferale, L. & Sbragaglia, M. 2005 Dynamical scaling and intermittency in shell models of turbulence. Phys. Rev. E 71, 065302.CrossRefGoogle ScholarPubMed
Biferale, L. 2003 Shell models of energy cascade in turbulence. Annu. Rev. Fluid Mech. 35, 441–468.CrossRefGoogle Scholar
Biferale, L., Musacchio, S. & Toschi, F. 2012 Inverse energy cascade in three-dimensional isotropic turbulence. Phys. Rev. Lett. 108, 164501.CrossRefGoogle ScholarPubMed
Biferale, L., Pierotti, D. & Toschi, F. 1998 Helicity transfer in turbulent models. Phys. Rev. E 57, R2515–R2518.Google Scholar
Biferale, L. & Procaccia, I. 2005 Anisotropy in turbulent flows and in turbulent transport. Phys. Rep. 414, 43–164.Google Scholar
Biferale, L. & Titi, E. 2013 On the global regularity of a helical-decimated version of the 3D Navier–Stokes equations. J. Stat. Phys. 151, 1089–1098.CrossRefGoogle Scholar
Boffetta, G. & Ecke, R. E. 2012 Two-dimensional turbulence. Annu. Rev. Fluid Mech. 44, 427–451.Google Scholar
Boffetta, G. & Musacchio, S. 2010 Evidence for the double cascade scenario in two-dimensional turbulence. Phys. Rev. E 82, 016307.CrossRefGoogle ScholarPubMed
Brandenburg, A. 2008 The inverse cascade and nonlinear alpha-effect in simulations of isotropic helical hydromagnetic turbulence. Astrophys. J. 550, 824–840.Google Scholar
Brissaud, A., Frisch, U., Leorat, J., Lesieur, M. & Mazure, M. 1973 Helicity cascades in fully developed isotropic turbulence. Phys. Fluids 16, 1366–1367.Google Scholar
Celani, A., Musacchio, S. & Vincenzi, D. 2010 Turbulence in more than two and less than three dimensions. Phys. Rev. Lett. 104, 184506.Google Scholar
Cencini, M., Muratore-Ginanneschi, P. & Vulpiani, A. 2011 Nonlinear superposition of direct and inverse cascades in two-dimensional turbulence forced at large and small scales. Phys. Rev. Lett. 107, 174502.Google Scholar
Chen, Q., Chen, S. & Eyink, G. L. 2003a The joint cascade of energy and helicity in three-dimensional turbulence. Phys. Fluids 15, 361–374.Google Scholar
Chen, Q., Chen, S., Eyink, G. L & Holm, D. D. 2003b Intermittency in the joint cascade of energy and helicity. Phys. Rev. Lett. 90, 214503.Google Scholar
Chkhetiani, O. G. 1996 On the third moments in helical turbulence. J. Expl Theor. Phys. Lett. 63, 808–812.Google Scholar
Clercx, H. J. H. & van Heijst, G. J. F. 2009 Two-dimensional Navier–Stokes turbulence in bounded domains. Appl. Mech. Rev. 62, 020802.Google Scholar
Constantin, P. & Majda, A. 1988 The Beltrami spectrum for incompressible fluid flows. Commun. Math. Phys. 115, 435–456.Google Scholar
Ditlevsen, P. D. 1997 Cascades of energy and helicity in the GOY shell model of turbulence. Phys. Fluids 9, 1482–1484.CrossRefGoogle Scholar
Dubief, Y., Terrapon, V. E. & Soria, J. 2013 On the mechanism of elasto-inertial turbulence. arXiv:1301.3952v1.Google Scholar
Eyink, G. L. & Sreenivasan, K. R. 2006 Onsager and the theory of hydrodynamic turbulence. Rev. Mod. Phys. 78, 87–135.Google Scholar
Falkovich, G., Fouxon, I. & Oz, Y. 2010 New relations for correlation functions in Navier–Stokes turbulence. J. Fluid Mech. 644, 465–472.Google Scholar
Francois, N., Xia, H., Punzmann, H. & Shats, M. 2013 Inverse energy cascade and emergence of large-scale coherent vortices in turbulence driven by Faraday waves. arXiv:1302.2993.Google Scholar
Frisch, U. 1995 Turbulence: The Legacy of A. N. Kolmogorov. Cambridge University Press.Google Scholar
Frisch, U., Pomyalov, A., Procaccia, I. & Ray, S. S. 2012 Turbulence in non-integer dimensions by fractal Fourier decimation. Phys. Rev. Lett. 108, 074501.Google Scholar
Grossmann, S., Lohse, D & Reeh, A. 1996 Developed turbulence: from full simulations to full mode reductions. Phys. Rev. Lett. 77, 5369–5372.Google Scholar
Herbert, E., Daviaud, F., Dubrulle, B., Nazarenko, S. & Naso, A. 2012 Dual non-Kolmogorov cascades in a von Kármán flow. Europhys. Lett. 100, 44003.Google Scholar
Huang, N. E. & Shen, S. S. 2005 Hilbert–Huang Transform and its Applications. World Scientific.Google Scholar
Kraichnan, R. H. 1967 Inertial ranges in two-dimensional turbulence. Phys. Fluids 10, 1417–1423.Google Scholar
Kraichnan, R. H. 1973 Helical turbulence and absolute equilibrium. J. Fluid Mech. 59, 745–752.CrossRefGoogle Scholar
Lautenschlager, M., Eppel, D. P. & Thacker, W. C. 1998 Subgrid parametrization in helical flows. Beitr. Phys. Atmos. 61, 87–97.Google Scholar
Laval, J.-P., Dubrulle, B. & Nazarenko, S. 2001 Nonlocality and intermittency in three-dimensional turbulence. Phys. Fluids 13, 1995–2012.Google Scholar
Lessinnes, T., Plunian, F. & Carati, D. 2009 Helical shell models for MHD. Theor. Comput. Fluid Dyn. 23, 439–450.CrossRefGoogle Scholar
Mininni, P. D. 2011 Scale interactions in magnetohydrodynamic turbulence. Annu. Rev. Fluid Mech. 43, 377–397.Google Scholar
Mininni, P. D., Alexakis, A. & Pouquet, A. 2009 Scale interactions and scaling laws in rotating flows at moderate Rossby numbers and large Reynolds numbers. Phys. Fluids 21, 015108.Google Scholar
Mininni, P. D. & Pouquet, A. 2010 Rotating helical turbulence. Part 2. Intermittency, scale invariance, and structures. Phys. Fluids 22, 035105.Google Scholar
Mininni, P. D. & Pouquet, A. 2013 Inverse cascade behaviour in freely decaying two-dimensional fluid turbulence. arXiv:1302.2988.Google Scholar
Moffat, H. K. 1969 The degree of knottedness of tangled vortex lines. J. Fluid Mech. 35, 117–129.Google Scholar
Nastrom, S. G., Gage, K. S. & Jasperson, W. H. 1984 Kinetic energy spectrum of large- and mesoscale atmospheric processes. Nature 310, 36–38.Google Scholar
Paret, J. & Tabeling, P. 1998 Intermittency in the two-dimensional inverse cascade of energy: experimental observations. Phys. Fluids 10, 3126–3136.Google Scholar
Pelz, R. B., Shtilman, L. & Tsinober, A. 1986 The helical nature of unforced turbulent flows. Phys. Fluids 29, 3506–3508.Google Scholar
Pelz, R. B., Yakhot, V., Orszag, S. A., Shtilman, L. & Levich, E. 1985 Velocity–vorticity patterns in turbulent flow. Phys. Rev. Lett. 54, 2505–2508.CrossRefGoogle ScholarPubMed
Smith, L. M., Chasnov, J. R. & Waleffe, F. 1996 Crossover from two- to three-dimensional turbulence. Phys. Rev. Lett. 77, 2467–2470.Google Scholar
Smith, L. M. & Waleffe, F. 1999 Transfer of energy to two-dimensional large scales in forced, rotating three-dimensional turbulence. Phys. Fluids 11, 1608–1622.CrossRefGoogle Scholar
Sulem, P. L., She, Z. S., Scholl, H. & Frisch, U. 1989 Generation of large-scale structures in three-dimensional flow lacking parity-invariance. J. Fluid Mech. 205, 341–358.Google Scholar
Vorobieff, P., Rivera, M. & Ecke, R. E. 1999 Soap film flows: statistics of two-dimensional turbulence. Phys. Fluids 11, 2167–2177.Google Scholar
Waleffe, F. 1992 The nature of triad interactions in homogeneous turbulence. Phys. Fluids A 4, 350–363.Google Scholar
Xia, H., Byrne, D., Falkovich, G. & Shats, M. G. 2011 Upscale energy transfer in thick turbulent fluid layers. Nature Phys. 7, 321–324.CrossRefGoogle Scholar
Xia, H., Punzmann, H., Falkovich, G. & Shats, M. G. 2008 Turbulence–condensate interaction in two dimensions. Phys. Rev. Lett. 101, 194504.Google Scholar