Hostname: page-component-745bb68f8f-f46jp Total loading time: 0 Render date: 2025-01-09T21:58:24.051Z Has data issue: false hasContentIssue false
  • English
  • Français

Spin-down in rotating Hagen–Poiseuille flow: a simple criterion to detect the onset of absolute instabilities

Published online by Cambridge University Press:  16 March 2016

A. Miranda-Barea ,
C. Fabrellas-García ,
L. Parras  and
C. del Pino
A. Miranda-Barea
Affiliation:
Universidad de Málaga, E.T.S. Ingeniería Industrial, Campus de Teatinos, 29071, Málaga, Spain
C. Fabrellas-García
Affiliation:
Universidad de Málaga, E.T.S. Ingeniería Industrial, Campus de Teatinos, 29071, Málaga, Spain
L. Parras
Affiliation:
Universidad de Málaga, E.T.S. Ingeniería Industrial, Campus de Teatinos, 29071, Málaga, Spain
C. del Pino*
Affiliation:
Universidad de Málaga, E.T.S. Ingeniería Industrial, Campus de Teatinos, 29071, Málaga, Spain
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We conduct experiments in a circular pipe with rotating Hagen–Poiseuille flow (RHPF) to which we apply spin-down or impulsive spin-down to rest, in order to analyse the threshold between convective and absolute instabilities through flow visualisations in the inlet region of the pipe. For a constant value of the Reynolds number, 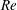$Re$, the finite-amplitude wave packets generated by the arbitrary perturbation that results by reducing the swirl parameter, propagate upstream or downstream depending on the initial value of the swirl parameter, 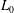$L_{0}$. In fact, the main characteristic of the flow is that the velocity front of these wave packets changes from negative to positive when absolutely unstable modes are present in the initial state. The experimental results show that spin-down becomes a precise, reliable procedure to detect the onset of absolute instabilities. In addition, we give evidence of a gradual transition for Reynolds numbers ranging from 300 to 500 where a mode shift from 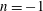$n=-1$ to 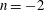$n=-2$ appears in the absolutely unstable region.

JFM classification

Instability: Absolute/convective instability Instability: Instability
Type
Papers
Information
Journal of Fluid Mechanics , Volume 793 , 25 April 2016 , pp. 316 - 334
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Barnes, D. R. & Kerswell, R. R. 2000 New results in rotating Hagen–Poiseuille flow. J. Fluid Mech. 417, 103–126.Google Scholar
Bers, A. 1975 Linear waves and instabilities. In Physique des Plasmas, pp. 117–215. Gordon and Breach Science Publishers.Google Scholar
Bien, F. & Penner, S. S. 1971 Spin-up and spin-down of rotating flows in finite cylindrical containers. Phys. Fluids 14, 1305–1308.CrossRefGoogle Scholar
Briggs, R. J. 1964 Electron–Steam Interaction with Plamas. MIT Press.Google Scholar
Chomaz, J.-M. 2003 Fully nonlinear dynamics of parallel wakes. J. Fluid Mech. 495, 57–75.Google Scholar
Clark, A., Clark, P. A., Thomas, J. H. & Nien-Hon, L. 1971 Spin-up of a strongly stratified fluid in a sphere. J. Fluid Mech. 45, 131–149.Google Scholar
Cui, X. 2003 A numerical study of the recirculation zones during spin-up and spin-down for confined rotating flows. J. Theor. Comput. Fluid Dyn. 17, 31–49.CrossRefGoogle Scholar
Delbende, I. & Chomaz, J.-M. 1998a Absolute/convective instabilities in the Batchelor vortex: a numerical study of the linear impulsive response. J. Fluid Mech. 355, 229–254.Google Scholar
Delbende, I. & Chomaz, J.-M. 1998b Nonlinear convective/absolute instabilities in parallel two-dimensional wakes. Phys. Fluids 10 (11), 2724–2736.CrossRefGoogle Scholar
Dolzhanskii, F. V., Krymov, V. A. & Manin, D. Yu. 1992 Self-similar spin-up and spin-down in a cylinder of small ratio of height to diameter. J. Fluid Mech. 234, 473–486.Google Scholar
Duck, P. W. & Foster, M. R. 2001 Spin-up of homogeneous and stratified fluids. Annu. Rev. Fluid Mech. 33, 231–236.Google Scholar
Fernandez-Feria, R. & del Pino, C. 2002 The onset of absolute instability of rotating Hagen–Poiseuille flow: a spatial stability analysis. Phys. Fluids 14 (9), 3087–3097.CrossRefGoogle Scholar
Greenspan, H. P. & Howard, N. 1963 On a time-dependent motion of a rotating fluid. J. Fluid Mech. 17, 385–404.Google Scholar
Heaton, C. J. 2008 On the inviscid neutral curve of rotating Poiseuille pipe flow. Phys. Fluids 20, 024105.Google Scholar
Hewitt, R. E., Hazel, A. L., Clarke, R. J. & Denier, J. P. 2011 Unsteady flow in a rotating torus after a sudden change in rotation rate. J. Fluid Mech. 688, 88–119.Google Scholar
Huerre, P. & Monkewitz, P. A. 1998 Local and global instabilities in spatially developing flows. Annu. Rev. Fluid Mech. 22, 473–537.CrossRefGoogle Scholar
Imao, S., Itoh, M., Yamada, Y. & Zhang, Q. 1992 The characteristics of spriral waves in an axially rotating pipe. Exp. Fluids 12, 277–285.Google Scholar
Imao, S., Zhang, Q. & Yamada, Y. 1989 The laminar flow in the developing region of a rotating pipe. JSME Intl J. 32 (3), 317–323.Google Scholar
Krymov, V. A. 1990 Spin-up in a shallow cylinder. Fluid Dyn. 25, 845–850.Google Scholar
Krymov, V. A. & Manin, D. Yu. 1986 Spin-down of a fluid in a low cylinder at large reynolds numbers. Fluid Dyn. 21, 369–376.Google Scholar
Kühnen, J., Holzner, M., Hof, B. & Kuhlmann, H. C. 2013 Experimental investigation of transitional flow in a toroidal pipe. J. Fluid Mech. 738, 463–491.Google Scholar
Lingwood, R. J. 1996 An experimental study of absolute instability of the rotating-disk boundary-layer flow. J. Fluid Mech. 314, 373–405.Google Scholar
Lingwood, R. J. 1997a Absolute instability of the ekman layer and related rotating flows. J. Fluid Mech. 331, 405–428.Google Scholar
Lingwood, R. J. 1997b On the effects of suction and injection on the absolute instability of the rotating-disk boundary layer. Eur. J. Mech. (B/Fluids) 9 (5), 1317–1328.Google Scholar
Lingwood, R. J. & Garrett, S. J. 2011 The effects of surface mass flux on the instability of the bek system of rotating boundary layer flows. Eur. J. Mech. (B/Fluids) 30, 299–310.CrossRefGoogle Scholar
Lopez, J. M. & Weidman, P. D. 1996 Stability of stationary endwall boundary layers during spin-down. J. Fluid Mech. 326, 373–398.Google Scholar
Madden, F. N. & Mullin, T. 1994 The spin-up from rest of a fluid-filled torus. J. Fluid Mech. 265, 217–244.CrossRefGoogle Scholar
Mathis, D. M. & Neitzel, G. P. 1985 Experiments on impulsive spindown to rest. Phys. Fluids 28, 449.CrossRefGoogle Scholar
Maxworthy, T. & Browand, F. K. 1975 Experiments in rotating and stratified flows: Oceanographic application. Annu. Rev. Fluid Mech. 7, 273–305.Google Scholar
Miranda-Barea, A., Martínez-Arias, B., Parras, L., Burgos, M. A. & del Pino, C. 2015 Experimental study of rotating Hagen–Poiseuille flow discharging into a 1:8 sudden expansion. Phys. Fluids 27 (3), 034104.Google Scholar
Neitzel, G. P. & Davis, S. H. 1981 Centrifugal instabilities during spin-down to rest in finite cylinders. Numerical experiments. J. Fluid Mech. 102, 329–352.Google Scholar
Ogawa, A. & Murakami, H. 2004 Spin-up and spin-down times of rotational air flow depended on mean air velocity and surface roughness on inner surface in cylindrical vortex chamber. J. Thermal Sci. 13, 46–55.Google Scholar
Park, J. S. & Hyun, J. M. 2008 Review on open-problems of spin-up flow of an incompressible fluid. J. Mech. Sci. Tech. 22 (4), 780–787.CrossRefGoogle Scholar
Pedley, T. J. 1969 On the instability of viscous flow in a rapidly rotating pipe. J. Fluid Mech. 35, 97–115.Google Scholar
del Pino, C., Hewitt, R. E., Clarke, R. J., Mullin, T. & Denier, J. P. 2008 Unsteady fronts in the spin-down of a fluid-filled torus. Phys. Fluids 20, 124104.Google Scholar
del Pino, C., Ortega-Casanova, J. & Fernandez-Feria, R. 2003 Nonparallel stability of the flow in an axially rotating pipe. Fluid Dyn. Res. 32, 261–281.Google Scholar
Sakurai, T. 1969 Spin down problem of rotating stratified fluid in thermally insulated circular cylinders. J. Fluid Mech. 37, 689–699.Google Scholar
Sanmiguel-Rojas, E. & Fernandez-Feria, R. 2005 Nonlinear waves in the pressure driven flow in a finite rotating pipe. Phys. Fluids 17, 014104.Google Scholar
Savas, Ö. 1985 On flow visualization using reflective flakes. J. Fluid Mech. 152, 235–248.Google Scholar
Shrestha, K., Parras, L., del Pino, C., Sanmiguel-Rojas, E. & Fernandez-Feria, R. 2013 Experimental evidence of convective and absolute instabilities in rotating Hagen–Poiseuille flow. J. Fluid Mech. 417, 103–126.Google Scholar
Suslov, S. A. 2006 Numerical aspects of searching convective/absolute instability transition. J. Comput. Phys. 212, 188–217.Google Scholar
Wedemeyer, H. 1964 The unsteady flow within a spinning cylinder. J. Fluid Mech. 20, 383–399.Google Scholar
Weidman, P. D. 1976 On the spin-up and spin-down of a rotating fluid. I – extending the Wedemeyer model. II – measurements and stability. J. Fluid Mech. 77, 685–735.Google Scholar

Miranda-Barea et al. supplementary movie

Spin-down in rotating Hagen-Poiseuille flow is applied to detect by means of direct observation the onset of absolute instabilities. In this video, and for a constant Reynolds number of 250, we reduce suddenly the angular velocity to 50 %. The flow is convectively and absolutely unstable in the first and second sequences, respectively, thus producing different flow patterns in the temporal evolution of the perturbation-produced wave packet fronts in the pipe inlet region.

Download Miranda-Barea et al. supplementary movie(Video)
Video 21 MB