Hostname: page-component-745bb68f8f-mzp66 Total loading time: 0 Render date: 2025-02-11T12:29:14.207Z Has data issue: false hasContentIssue false
  • English
  • Français

Spin-down in a rapidly rotating cylinder container with mixed rigid and stress-free boundary conditions

Published online by Cambridge University Press:  30 March 2017

L. Oruba ,
A. M. Soward Open the ORCID record for A. M. Soward [Opens in a new window]  and
E. Dormy
L. Oruba
Affiliation:
Département de Physique, École Normale Supérieure, 24 rue Lhomond, 75005 Paris, France
A. M. Soward*
Affiliation:
School of Mathematics and Statistics, Newcastle University, Newcastle upon Tyne NE1 7RU, UK
E. Dormy*
Affiliation:
Département de Mathématiques et Applications, UMR-8553, École Normale Supérieure, 45 rue d’Ulm, 75005 Paris, France
*
†Email addresses for correspondence: [email protected], [email protected], [email protected]
†Email addresses for correspondence: [email protected], [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A comprehensive study of the classical linear spin-down of a constant-density viscous fluid (kinematic viscosity $\unicode[STIX]{x1D708}$) rotating rapidly (angular velocity 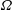$\unicode[STIX]{x1D6FA}$) inside an axisymmetric cylindrical container (radius 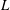$L$, height 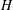$H$) with rigid boundaries, which follows the instantaneous small change in the boundary angular velocity at small Ekman number 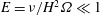$E=\unicode[STIX]{x1D708}/H^{2}\unicode[STIX]{x1D6FA}\ll 1$, was provided by Greenspan & Howard (J. Fluid Mech., vol. 17, 1963, pp. 385–404). For that problem 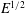$E^{1/2}$ Ekman layers form quickly, triggering inertial waves together with the dominant spin-down of the quasi-geostrophic (QG) interior flow on the 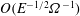$O(E^{-1/2}\unicode[STIX]{x1D6FA}^{-1})$ time scale. On the longer lateral viscous diffusion time scale 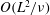$O(L^{2}/\unicode[STIX]{x1D708})$, the QG flow responds to the 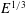$E^{1/3}$ sidewall shear layers. In our variant, the sidewall and top boundaries are stress-free, a set-up motivated by the study of isolated atmospheric structures such as tropical cyclones or tornadoes. Relative to the unbounded plane layer case, spin-down is reduced (enhanced) by the presence of a slippery (rigid) sidewall. This is evidenced by the QG angular velocity, 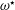$\unicode[STIX]{x1D714}^{\star }$, evolution on the 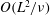$O(L^{2}/\unicode[STIX]{x1D708})$ time scale: spatially, 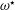$\unicode[STIX]{x1D714}^{\star }$ increases (decreases) outwards from the axis for a slippery (rigid) sidewall; temporally, the long-time 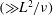$(\gg L^{2}/\unicode[STIX]{x1D708})$ behaviour is dominated by an eigensolution with a decay rate slightly slower (faster) than that for an unbounded layer. In our slippery sidewall case, the 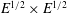$E^{1/2}\times E^{1/2}$ corner region that forms at the sidewall intersection with the rigid base is responsible for a 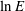$\ln E$ singularity within the 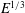$E^{1/3}$ layer, causing our asymptotics to apply only at values of 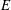$E$ far smaller than can be reached by our direct numerical simulation (DNS) of the linear equations governing the entire spin-down process. Instead, we solve the 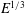$E^{1/3}$ boundary layer equations for given 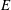$E$ numerically. Our hybrid asymptotic–numerical approach yields results in excellent agreement with our DNS.

JFM classification

Boundary Layers: Boundary Layers Geophysical and Geological Flows: Geophysical and Geological Flows Geophysical and Geological Flows: Rotating flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 818 , 10 May 2017 , pp. 205 - 240
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abramowitz, M. & Stegun, I. A. 2010 NIST Handbook of Mathematical Functions (ed. Olver, F. W. J., Lozier, D. W., Boisvert, R. F. & Clark, C. W.), Cambridge University Press; available online http://dlmf.nist.gov/.Google Scholar
Barcilon, V. 1968 Stewartson layers in transient rotating fluid flows. J. Fluid Mech. 33, 815–825.Google Scholar
Benton, E. R. & Clark, A. 1974 Spin-up. Annu. Rev. Fluid Mech. 6, 257–280.Google Scholar
Chelton, D. B., Schlax, M. G. & Samelson, R. M. 2011 Global observations of nonlinear mesoscale eddies. Prog. Oceanogr. 91, 167–216.Google Scholar
Dormy, E. & Soward, A. M. 2007 Mathematical aspects of natural dynamos. In The Fluid Mechanics of Astrophysics and Geophysics (ed. Soward, A. M. & Ghil, M.), vol. 13, pp. 120–136. Chapman & Hall.Google Scholar
Duck, P. W. & Foster, M. R. 2001 Spin-up of homogeneous and stratified fluids. Annu. Rev. Fluid Mech. 33, 231–263.Google Scholar
Erdélyi, A., Magnus, W., Oberhettinger, F. & Triconi, F. G. 1953 Higher Transcendetal Functions, Vol. II. Bateman Manuscript Project. McGraw-Hill.Google Scholar
Greenspan, H. P. 1968 The Theory of Rotating Fluids. Cambridge University Press.Google Scholar
Greenspan, H. P. & Howard, L. N. 1963 On a time-dependent motion of a rotating fluid. J. Fluid Mech. 17, 385–404.Google Scholar
Hinch, E. J. 1991 Perturbation Methods, Cambridge Texts in Applied Mathematics. Cambridge University Press.Google Scholar
Hyun, J. M., Leslie, F., Fowlis, W. W. & Warn-Varnas, A. 1983 Numerical solutions for spin-up from rest in a cylinder. J. Fluid Mech. 127, 263–281.Google Scholar
Kerswell, R. R. & Barenghi, C. F. 1995 On the viscous decay rates of inertial waves in a rotating circular cylinder. J. Fluid Mech. 285, 203–214.Google Scholar
Marcotte, F., Dormy, E. & Soward, A. M. 2016 On the equatorial Ekman layer. J. Fluid Mech. 803, 395–435.Google Scholar
Montgomery, M. T., Snell, H. D. & Yang, Z. 2001 Axisymmetric spindown dynamics of hurricane-like vortices. J. Atmos. Sci. 58, 421–435.Google Scholar
Moore, D. W. & Saffman, P. G. 1969 The structure of free vertical shear layers in a rotating fluid and the motion produced by a slowly rising body. Phil. Trans. R. Soc. Lond. A 264 (1156), 597–634.Google Scholar
Oruba, L., Davidson, P. & Dormy, E. 2017 Eye formation in rotating convection. J. Fluid Mech. 812, 890–904.Google Scholar
Park, J. S. & Hyun, J. M. 1997 Transient Stewartson layers of a rotating compressible fluid. Fluid Dyn. Res. 19, 303–325.Google Scholar
Persing, J., Montgomery, M. T., Smith, R. K. & McWilliams, J. C. 2015 On the realism of quasi steady-state hurricanes. Q. J. R. Meteorol. Soc. 141, 1–14.Google Scholar
Read, P. L. 1986a Super-rotation and diffusion of axial angular momentum. I. ‘Speed limits’ for axisymmetric flow in a rotating cylindrical fluid annulus. Q. J. R. Meteorol. Soc. 112, 231–251.Google Scholar
Read, P. L. 1986b Super-rotation and diffusion of axial angular momentum. II. A review of quasi-axisymmetric models of planetary atmospheres. Q. J. R. Meteorol. Soc. 112, 253–272.Google Scholar
Smith, R. K. & Montgomery, M. T. 2010 Hurricane boundary-layer theory. Q. J. R. Meteorol. Soc. 136, 1665–1670.Google Scholar
Stewartson, K. 1957 On almost rigid rotations. J. Fluid Mech. 3, 17–26.Google Scholar
Watson, G. N. 1966 A Treatise on the Theory of Bessel Functions. Cambridge University Press.Google Scholar
Wedemeyer, E. H. 1964 The unsteady flow within a spinning cylinder. J. Fluid Mech. 20, 383–399.Google Scholar
Williams, G. P. 1968 Thermal convection in a rotating fluid annulus: part 3. Suppression of the frictional constraint on lateral boundaries. J. Atmos. Sci. 25, 1034–1045.Google Scholar
Zhang, K. & Liao, X. 2008 On the initial-value problem in a rotating circular cylinder. J. Fluid Mech. 610, 425–443.Google Scholar