Published online by Cambridge University Press: 21 April 2015
One-dimensional energy spectra in flat plate zero pressure gradient boundary layers and pipe flows are examined over a wide range of Reynolds numbers (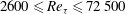 $2600\leqslant \mathit{Re}_{{\it\tau}}\leqslant 72\,500$). The spectra show excellent collapse with Kolmogorov scaling at high wavenumbers for both flows at all Reynolds numbers. The peaks associated with the large-scale motions (LSMs) and superstructures (SS) in boundary layers behave as they do in pipe flows, with some minor differences. The location of the outer spectral peak, associated with SS or very large-scale motions (VLSMs) in the turbulent wall region, displays only a weak dependence on Reynolds number, and it occurs at the same wall-normal distance where the variances establish a logarithmic behaviour and where the amplitude modulation coefficient has a zero value. The results suggest that with increasing Reynolds number the energy is largely confined to a thin wall layer that continues to diminish in physical extent. The outer-scaled wavelength of the outer spectral peak appears to decrease with increasing Reynolds number. However, there is still significant energy content in wavelengths associated with the SS and VLSMs. The location of the outer spectral peak appears to mark the start of a plateau that is consistent with a
$2600\leqslant \mathit{Re}_{{\it\tau}}\leqslant 72\,500$). The spectra show excellent collapse with Kolmogorov scaling at high wavenumbers for both flows at all Reynolds numbers. The peaks associated with the large-scale motions (LSMs) and superstructures (SS) in boundary layers behave as they do in pipe flows, with some minor differences. The location of the outer spectral peak, associated with SS or very large-scale motions (VLSMs) in the turbulent wall region, displays only a weak dependence on Reynolds number, and it occurs at the same wall-normal distance where the variances establish a logarithmic behaviour and where the amplitude modulation coefficient has a zero value. The results suggest that with increasing Reynolds number the energy is largely confined to a thin wall layer that continues to diminish in physical extent. The outer-scaled wavelength of the outer spectral peak appears to decrease with increasing Reynolds number. However, there is still significant energy content in wavelengths associated with the SS and VLSMs. The location of the outer spectral peak appears to mark the start of a plateau that is consistent with a 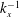 $k_{x}^{-1}$ slope in the spectrum and the logarithmic variation in the variances. This
$k_{x}^{-1}$ slope in the spectrum and the logarithmic variation in the variances. This 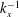 $k_{x}^{-1}$ region seems to occur when there is sufficient scale separation between the locations of the outer spectral peak and the outer edge of the log region. It does not require full similarity between outer and wall-normal scaling on the wavenumber. The extent of
$k_{x}^{-1}$ region seems to occur when there is sufficient scale separation between the locations of the outer spectral peak and the outer edge of the log region. It does not require full similarity between outer and wall-normal scaling on the wavenumber. The extent of 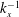 $k_{x}^{-1}$ region depends on the wavelength of the outer spectral peak (
$k_{x}^{-1}$ region depends on the wavelength of the outer spectral peak (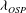 ${\it\lambda}_{OSP}$), which appears to emerge as a new length scale for the log region. Finally, based on the observations from the spectra together with the statistics presented in Vallikivi et al. (J. Fluid Mech., 2015 (submitted)), five distinct wall-normal layers are identified in turbulent wall flows.
${\it\lambda}_{OSP}$), which appears to emerge as a new length scale for the log region. Finally, based on the observations from the spectra together with the statistics presented in Vallikivi et al. (J. Fluid Mech., 2015 (submitted)), five distinct wall-normal layers are identified in turbulent wall flows.