Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-23T15:32:23.989Z Has data issue: false hasContentIssue false
  • English
  • Français

Spectral non-locality, absolute equilibria and Kraichnan–Leith–Batchelor phenomenology in two-dimensional turbulent energy cascades

Published online by Cambridge University Press:  14 May 2013

B. H. Burgess  and
T. G. Shepherd
B. H. Burgess*
Affiliation:
Department of Physics, University of Toronto, Toronto, ON, Canada M5S 1A7
T. G. Shepherd
Affiliation:
Department of Physics, University of Toronto, Toronto, ON, Canada M5S 1A7 Department of Meteorology, University of Reading, Reading, Berkshire RG6 6BB, UK
*
†Email address for correspondence: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study the degree to which Kraichnan–Leith–Batchelor (KLB) phenomenology describes two-dimensional energy cascades in $\alpha $ turbulence, governed by 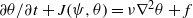$\partial \theta / \partial t+ J(\psi , \theta )= \nu {\nabla }^{2} \theta + f$, where 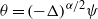$\theta = {(- \Delta )}^{\alpha / 2} \psi $ is generalized vorticity, and 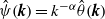$\hat {\psi } (\boldsymbol{k})= {k}^{- \alpha } \hat {\theta } (\boldsymbol{k})$ in Fourier space. These models differ in spectral non-locality, and include surface quasigeostrophic flow (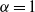$\alpha = 1$), regular two-dimensional flow (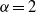$\alpha = 2$) and rotating shallow flow (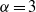$\alpha = 3$), which is the isotropic limit of a mantle convection model. We re-examine arguments for dual inverse energy and direct enstrophy cascades, including Fjørtoft analysis, which we extend to general $\alpha $, and point out their limitations. Using an $\alpha $-dependent eddy-damped quasinormal Markovian (EDQNM) closure, we seek self-similar inertial range solutions and study their characteristics. Our present focus is not on coherent structures, which the EDQNM filters out, but on any self-similar and approximately Gaussian turbulent component that may exist in the flow and be described by KLB phenomenology. For this, the EDQNM is an appropriate tool. Non-local triads contribute increasingly to the energy flux as $\alpha $ increases. More importantly, the energy cascade is downscale in the self-similar inertial range for 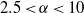$2. 5\lt \alpha \lt 10$. At 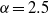$\alpha = 2. 5$ and 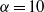$\alpha = 10$, the KLB spectra correspond, respectively, to enstrophy and energy equipartition, and the triad energy transfers and flux vanish identically. Eddy turnover time and strain rate arguments suggest the inverse energy cascade should obey KLB phenomenology and be self-similar for 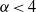$\alpha \lt 4$. However, downscale energy flux in the EDQNM self-similar inertial range for 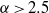$\alpha \gt 2. 5$ leads us to predict that any inverse cascade for $\alpha \geq 2. 5$ will not exhibit KLB phenomenology, and specifically the KLB energy spectrum. Numerical simulations confirm this: the inverse cascade energy spectrum for 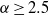$\alpha \geq 2. 5$ is significantly steeper than the KLB prediction, while for 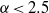$\alpha \lt 2. 5$ we obtain the KLB spectrum.

JFM classification

Turbulent Flows: Isotropic turbulence Turbulent Flows: Turbulent Flows Turbulent Flows: Turbulence theory
Type
Papers
Information
Journal of Fluid Mechanics , Volume 725 , 25 June 2013 , pp. 332 - 371
Creative Commons
Creative Common License - CCCreative Common License - BYCreative Common License - NCCreative Common License - SA
The online version of this article is published within an Open Access environment subject to the conditions of the Creative Commons Attribution-NonCommercial-ShareAlike licence . The written permission of Cambridge University Press must be obtained for commercial re-use.
Copyright
©2013 Cambridge University Press.

References

Batchelor, G. K. 1959 Small-scale variation of convected quantities like temperature in turbulent fluid. Part 1. General discussion and the case of small conductivity. J. Fluid Mech. 5, 113–133.Google Scholar
Batchelor, G. K. 1969 Computation of the energy spectrum in homogeneous two-dimensional turbulence. Phys. Fluids Suppl. II 12, 233–239.CrossRefGoogle Scholar
Benzi, R., Vitaletti, M. & Vulpiani, A. 1978 A variational principle for the statistical mechanics of fully developed turbulence. J. Phys. A: Math. Gen. 15, 883–895.Google Scholar
Blumen, W. 1978 Uniform potential vorticity flow. Part I. Theory of wave interactions and two-dimensional turbulence. J. Atmos. Sci. 35, 774–783.2.0.CO;2>CrossRefGoogle Scholar
Boffetta, G., De Lillo, F. & Musacchio, S. 2002 Inverse cascade in Charney–Hasegawa–Mima turbulence. Europhys. Lett. 59, 687–693.CrossRefGoogle Scholar
Boffetta, G. & Musacchio, S. 2010 Evidence for the double cascade scenario in two-dimensional turbulence. Phys. Rev. E 82, 016307.Google Scholar
Borue, V. 1994 Inverse energy cascade in stationary two-dimensional homogeneous turbulence. Phys. Rev. Lett. 72, 1475–1478.Google Scholar
Bowman, J. C., Krommes, J. A. & Ottaviani, M. 1993 The realizable Markovian closure. I. General theory, with application to three-wave dynamics. Phys. Fluids B 5, 3558–3589.Google Scholar
Carnevale, G. F., Frisch, U. & Salmon, R. 1981 H theorems in statistical fluid dynamics. J. Phys. A: Math. Gen. 14, 1701–1718.Google Scholar
Chen, S., Ecke, R. E., Eyink, G. L., Rivera, M., Wan, M. & Xiao, Z. 2006 Physical mechanism of the two-dimensional inverse energy cascade. Phys. Rev. Lett. 96, 084502.Google Scholar
Farazmand, M. M., Kevlahan, N. K.-R. & Protas, B. 2011 Controlling the dual cascade of two-dimensional turbulence. J. Fluid Mech. 668, 202–222.CrossRefGoogle Scholar
Fjørtoft, R. 1953 On the changes in the spectral distribution of kinetic energy for two-dimensional non-divergent flow. Tellus 5, 225–230.Google Scholar
Fox, D. G. & Orszag, S. A. 1973 Inviscid dynamics of two-dimensional turbulence. Phys. Fluids 16, 169–171.Google Scholar
Gkioulekas, E. & Tung, K. K. 2007 A new proof on net upscale energy cascade in two-dimensional and quasi-geostrophic turbulence. J. Fluid Mech. 576, 173–189.CrossRefGoogle Scholar
Held, I. M., Pierrehumbert, R. T., Garner, S. T. & Swanson, K. L. 1995 Surface quasi-geostrophic dynamics. J. Fluid Mech. 282, 1–20.Google Scholar
Herring, J. R. & McWilliams, J. C. 1985 Comparison of direct numerical simulation of two-dimensional turbulence with two-point closure: the effects of intermittency. J. Fluid Mech. 153, 229–242.Google Scholar
Iwayama, T., Shepherd, T. G. & Watanabe, T. 2002 An ‘ideal’ form of decaying two-dimensional turbulence. J. Fluid Mech. 456, 183–198.Google Scholar
Iwayama, T. & Watanabe, T. 2010 Green’s function for a generalized two-dimensional fluid. Phys. Rev. E 82, 036307.CrossRefGoogle ScholarPubMed
Kraichnan, R. H. 1958a Irreversible statistical mechanics of incompressible hydromagnetic turbulence. Phys. Rev. 109, 1407–1422.CrossRefGoogle Scholar
Kraichnan, R. H. 1958b Higher order interactions in homogeneous turbulence theory. Phys. Fluids Rev. 1, 358–359.Google Scholar
Kraichnan, R. H. 1959 The structure of isotropic turbulence at very high Reynolds numbers. J. Fluid Mech. 5, 497–543.CrossRefGoogle Scholar
Kraichnan, R. H. 1967 Inertial ranges in two-dimensional turbulence. Phys. Fluids 10, 1417–1423.Google Scholar
Kraichnan, R. H. 1971a An almost-Markovian Galilean-invariant turbulence model. J. Fluid Mech. 47, 513–524.CrossRefGoogle Scholar
Kraichnan, R. H. 1971b Inertial-range transfer in two- and three-dimensional turbulence. J. Fluid Mech. 47, 525–535.Google Scholar
Kraichnan, R. H. 1975 Statistical dynamics of two-dimensional flow. J. Fluid Mech. 67, 155–175.CrossRefGoogle Scholar
Kraichnan, R. H. 1976 Eddy viscosity in two and three dimensions. J. Atmos. Sci. 33, 1521–1536.2.0.CO;2>CrossRefGoogle Scholar
Kraichnan, R. H. & Montgomery, D. 1980 Two-dimensionsional turbulence. Rep. Prog. Phys. 43, 547–619.CrossRefGoogle Scholar
Larichev, V. D. & McWilliams, J. C. 1991 Weakly decaying turbulence in an equivalent-barotropic fluid. Phys. Fluids A 3, 938–950.Google Scholar
Leith, C. E. 1968 Diffusion approximation for two-dimensional turbulence. Phys. Fluids 11, 671–673.Google Scholar
Leith, C. E. 1971 Atmospheric predictability and two-dimensional turbulence. J. Atmos. Sci. 28, 145–161.Google Scholar
Lesieur, M. 1993 Turbulence in Fluids, 2nd edn. Kluwer.Google Scholar
Leslie, D. C. 1973 Developments in the Theory of Turbulence. Oxford University Press.Google Scholar
Martin, P. C., Siggia, E. D. & Rose, H. A. 1973 Statistical dynamics of classical systems. Phys. Rev. A 8, 423–437.CrossRefGoogle Scholar
McComb, W. D. 1991 The Physics of Fluid Turbulence. Oxford University Press.Google Scholar
Merilees, P. E. & Warn, H. 1975 On energy and enstrophy exchanges in two-dimensional non-divergent flow. J. Fluid Mech. 69, 625–630.CrossRefGoogle Scholar
Orszag, S. A. 1970 Analytical theories of turbulence. J. Fluid Mech. 41, 363–386.Google Scholar
Orszag, S. A. 1977 Statistical Theory of Turbulence in Fluid Dynamics 1973 Les Houches Summer School of Theoretical Physics (ed. Balian, R. & Peube, J. L.). Gordon and Breach.Google Scholar
Paret, J. & Tabeling, P. 1997 Experimental observation of the two-dimensional inverse energy cascade. Phys. Rev. Lett. 79, 4162.CrossRefGoogle Scholar
Paret, J. & Tabeling, P. 1998 Intermittency in the two-dimensional inverse cascade of energy. Phys. Fluids 10, 3126–3136.CrossRefGoogle Scholar
Pierrehumbert, R. T., Held, I. M. & Swanson, K. L. 1994 Spectra of local and non-local two-dimensional turbulence. Chaos Solitons Fractals 4, 1111–1116.Google Scholar
Rhines, P. 1975 Waves and turbulence on a beta-plane. J. Fluid Mech. 69, 417–443.Google Scholar
Rhines, P. 1979 Geostrophic turbulence. Annu. Rev. Fluid Mech. 11, 401–441.Google Scholar
Salmon, R., Holloway, G. & Hendershott, M. C. 1976 The equilibrium statistical mechanics of simple quasi-geostrophic models. J. Fluid Mech. 75, 691–703.CrossRefGoogle Scholar
Salmon, R. 1998 Lectures on Geophysical Fluid Dynamics. Oxford University Press.CrossRefGoogle Scholar
Schorghofer, N. 2000 Energy spectra of steady two-dimensional turbulent flows. Phys. Rev. E 61, 6572–6577.Google Scholar
Scott, R. K. 2007 Nonrobustness of the two-dimensional turbulent inverse cascade. Phys. Rev. E 75, 046301.CrossRefGoogle ScholarPubMed
Smith, K. S., Boccaletti, G., Henning, C. C., Marinov, I., Tam, C. Y., Held, I. M. & Vallis, G. K. 2002 Turbulent diffusion in the geostrophic inverse cascade. J. Fluid Mech. 469, 13–48.Google Scholar
Smith, L. M. & Yakhot, V. 1994 Finite-size effects in forced two-dimensional turbulence. J. Fluid Mech. 274, 115–138.Google Scholar
Tran, C. V. 2004 Nonlinear transfer and spectral distribution of energy in $\alpha $ turbulence. Physica D 191, 137–155.CrossRefGoogle Scholar
Tran, C. V., Dritschel, D. G. & Scott, R. K. 2010 Effective degrees of nonlinearity in a family of generalized models of two-dimensional turbulence. Phys. Rev. E 76, 046303.Google Scholar
Tung, K. & Welch, W. 2001 Remarks on Charney’s note on geostrophic turbulence. J. Atmos. Sci. 58, 2009–2012.2.0.CO;2>CrossRefGoogle Scholar
Vallgren, A. 2011 Infrared Reynolds number dependency of two-dimensional inverse energy cascade. J. Fluid Mech. 667, 463–473.CrossRefGoogle Scholar
Vallis, G. K. 1985 Remarks on the predictability properties of two- and three-dimensional flow. Q. J. R. Meteorol. Soc. 111, 1039–1047.Google Scholar
Vallis, G. K. 2006 Atmospheric and Oceanic Fluid Dynamics. Cambridge University Press.Google Scholar
Watanabe, T. & Iwayama, T. 2004 Unified scaling theory for local and non-local transfers in generalized two-dimensional turbulence. J. Phys. Soc. Japan 12, 3319–3330.Google Scholar
Watanabe, T. & Iwayama, T. 2007 Interacting scales and triad enstrophy transfers in generalized two-dimensional turbulence. Phys. Rev. E 81, 016301.Google Scholar
Weinstein, S. A., Olson, P. L. & Yuen, D. A. 1989 Time-dependent large aspect-ratio thermal convection in the Earth’s mantle. Geophys. Astrophys. Fluid Dyn. 47, 157–197.Google Scholar
Xiao, Z., Wan, M., Chen, S. & Eyink, G. L. 2009 Physical mechanism of the inverse energy cascade of two-dimensional turbulence: a numerical investigation. J. Fluid Mech. 619, 1–44.Google Scholar