Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-26T16:16:54.479Z Has data issue: false hasContentIssue false
  • English
  • Français

A spectral model for homogeneous shear-driven anisotropic turbulence in terms of spherically averaged descriptors

Published online by Cambridge University Press:  22 December 2015

Vincent Mons ,
Claude Cambon  and
Pierre Sagaut
Vincent Mons*
Affiliation:
Sorbonne Univ, UPMC Univ Paris 06, UMR 7190, Inst Jean Le Rond d’Alembert, F-75005, Paris, France CNRS, UMR 7190, Inst Jean Le Rond d’Alembert, F-75005, Paris, France
Claude Cambon
Affiliation:
Laboratoire de Mécanique des Fluides et d’Acoustique, Université de Lyon, École Centrale de Lyon and CNRS, UMR 5509, Écully, France
Pierre Sagaut
Affiliation:
Aix Marseille Universite, CNRS, Centrale Marseille, M2P2 UMR 7340, 13451 Marseille, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A nonlinear spectral model in terms of spherically averaged descriptors is derived for the prediction of homogeneous turbulence dynamics in the presence of arbitrary mean-velocity gradients. The governing equations for the tensor 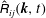$\hat{\unicode[STIX]{x1D619}}_{ij}(\boldsymbol{k},t)$, the Fourier transform of the two-point second-order correlation tensor, are first closed by an anisotropic eddy-damped quasinormal Markovian procedure. This closure is restricted to turbulent flows where linear effects induced by mean-flow gradients have no essential qualitative effects on the dynamics of triple correlations compared with the induced production effects in the equations for second-order correlations. Truncation at the first relevant order of spectral angular dependence allows us to derive from these equations in vector 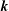$\boldsymbol{k}$ our final model equations in terms of the wavenumber modulus 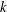$k$ only. Analytical spherical integration results in a significant decrease in computational cost. Besides, the model remains consistent with the decomposition in terms of directional anisotropy and polarization anisotropy, with a spherically averaged anisotropic spectral tensor for each contribution. Restriction of anisotropy to spherically averaged descriptors, however, entails a loss of information, and realizability conditions are considered to quantify the upper boundary of anisotropy that can be investigated with the proposed model. Several flow configurations are considered to assess the validity of the present model. Satisfactory agreement with experiments on grid-generated turbulence subjected to successive plane strains is observed, which confirms the capability of the model to account for production of anisotropy by mean-flow gradients. The nonlinear transfer terms of the model are further tested by considering the return to isotropy (RTI) of different turbulent flows. Different RTI rates for directional anisotropy and polarization anisotropy allow us to correctly predict the apparent delayed RTI shown after axisymmetric expansion. The last test case deals with homogeneous turbulence subjected to a constant pure plane shear. The interplay between linear and nonlinear effects is reproduced, yielding the eventual exponential growth of the turbulent kinetic energy.

JFM classification

Turbulent Flows: Homogeneous turbulence Turbulent Flows: Turbulence modelling Turbulent Flows: Turbulent Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 788 , 10 February 2016 , pp. 147 - 182
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

André, J. C. & Lesieur, M. 1977 Influence of helicity on the evolution of isotropic turbulence at high Reynolds number. J. Fluid Mech. 81, 187–207.Google Scholar
Bellet, F., Godeferd, F. S., Scott, J. F. & Cambon, C. 2006 Wave turbulence in rapidly rotating flows. J. Fluid Mech. 562, 83–121.Google Scholar
Brethouwer, G. 2005 The effect of rotation on rapidly sheared homogeneous turbulence and passive scalar transport. Linear theory and direct numerical simulation. J. Fluid Mech. 542, 305–342.Google Scholar
Cambon, C., Danaila, L., Godeferd, F. S. & Scott, J. F. 2013 Third-order statistics and the dynamics of strongly anisotropic turbulent flows. J. Turbul. 14 (3), 121–160.CrossRefGoogle Scholar
Cambon, C. & Jacquin, L. 1989 Spectral approach to non-isotropic turbulence subjected to rotation. J. Fluid Mech. 202, 295–317.Google Scholar
Cambon, C., Jeandel, D. & Mathieu, J. 1981 Spectral modelling of homogeneous non-isotropic turbulence. J. Fluid Mech. 104, 247–262.Google Scholar
Cambon, C., Mansour, N. N. & Godeferd, F. S. 1997 Energy transfer in rotating turbulence. J. Fluid Mech. 337, 303–332.CrossRefGoogle Scholar
Cambon, C. & Rubinstein, R. 2006 Anisotropic developments for homogeneous shear flows. Phys. Fluids 18, 085106.Google Scholar
Cambon, C. & Scott, J. F. 1999 Linear and nonlinear models of anisotropic turbulence. Annu. Rev. Fluid Mech. 31, 1–53.Google Scholar
Canuto, V. M. & Dubovikov, M. S. 1996a A dynamical model for turbulence. I. General formalism. Phys. Fluids 8 (2), 571–586.CrossRefGoogle Scholar
Canuto, V. M. & Dubovikov, M. S. 1996b A dynamical model for turbulence. II. Shear-driven flows. Phys. Fluids 8 (2), 587–598.CrossRefGoogle Scholar
Canuto, V. M. & Dubovikov, M. S. 1996c A dynamical model for turbulence. III. Numerical results. Phys. Fluids 8 (2), 599–613.Google Scholar
Chasnov, J. R. 1995 The decay of axisymmetric homogeneous turbulence. Phys. Fluids 7 (3), 600–605.CrossRefGoogle Scholar
Chen, J., Meneveau, C. & Katz, J. 2006 Scale interactions of turbulence subjected to a straining–relaxation–destraining cycle. J. Fluid Mech. 562, 123–150.CrossRefGoogle Scholar
Choi, K.-S. & Lumley, J. L. 2001 The return to isotropy of homogeneous turbulence. J. Fluid Mech. 436, 59–84.CrossRefGoogle Scholar
Clark, T. T. & Zemach, C. 1995 A spectral model applied to homogeneous turbulence. Phys. Fluids 7 (7), 1674–1694.Google Scholar
Corrsin, S.1958 On local isotropy in turbulent shear flow. NACA RM 58B11.Google Scholar
Craft, T. J., Ince, N. Z. & Launder, B. E. 1996 Recent developments in second-moment closure for buoyancy-affected flows. Dyn. Atmos. Oceans 23, 99–114.Google Scholar
Craft, T. J. & Launder, B. E. 2001 Principles and performance of TCL-based second-moment closures. Flow Turbul. Combust. 66, 355–372.Google Scholar
Davidson, P. A., Okamoto, N. & Kaneda, Y. 2012 On freely decaying, anisotropic, axisymmetric Saffman turbulence. J. Fluid Mech. 706, 150–172.Google Scholar
Favier, B. F. N., Godeferd, F. S., Cambon, C., Delache, A. & Bos, W. J. T. 2011 Quasi-static magnetohydrodynamic turbulence at high Reynolds number. J. Fluid Mech. 681, 434–461.Google Scholar
Gence, J. N. 1983 Homogeneous turbulence. Annu. Rev. Fluid Mech. 15, 201–222.CrossRefGoogle Scholar
Gence, J. N. & Mathieu, J. 1979 On the application of successive plane strains to grid-generated turbulence. J. Fluid Mech. 93, 501–513.Google Scholar
Gence, J. N. & Mathieu, J. 1980 The return to isotropy of an homogeneous turbulence having been submitted to two successive plane strains. J. Fluid Mech. 101, 555–566.Google Scholar
Godeferd, F. S. & Cambon, C. 1994 Detailed investigation of energy transfers in homogeneous stratified turbulence. Phys. Fluids 6, 2084–2100.Google Scholar
Herring, J. R. 1974 Approach of axisymmetric turbulence to isotropy. Phys. Fluids 17 (5), 859–872.CrossRefGoogle Scholar
Isaza, J. C. & Collins, L. R. 2009 On the asymptotic behaviour of large-scale turbulence in homogeneous shear flow. J. Fluid Mech. 637, 213–239.CrossRefGoogle Scholar
Ishihara, T., Yoshida, K. & Kaneda, Y. 2002 Anisotropic velocity correlation spectrum at small scales in a homogeneous turbulent shear flow. Phys. Rev. Lett. 88, 154501,1–4.Google Scholar
Kaneda, Y. 1981 Renormalized expansions in the theory of turbulence with the use of the Lagrangian position function. J. Fluid Mech. 107, 131–145.Google Scholar
Kassinos, S. C. & Akylas, E. 2012 Advances in particle representation modeling of homogeneous turbulence: from the linear PRM version to the interacting viscoelastic IPRM. In ERCOFTAC Series, vol. 18, pp. 81–101.Google Scholar
Kassinos, S. C. & Reynolds, W. C. 1997 Advances in structure-based turbulence modeling. In Annual Research Briefs – Center for Turbulence Research, pp. 179–193.Google Scholar
Kassinos, S. C., Reynolds, W. C. & Rogers, M. M. 2001 One-point turbulence structure tensors. J. Fluid Mech. 428, 231–248.Google Scholar
Kim, S.-W. & Chen, C.-P. 1989 A multiple-time-scale turbulence model based on variable partitioning of the turbulent kinetic energy spectrum. Numer. Heat Transfer B 16, 193–211.CrossRefGoogle Scholar
Kraichnan, R. H. 1959 The structure of isotropic turbulence at very high Reynolds numbers. J. Fluid Mech. 5, 497–543.CrossRefGoogle Scholar
Kraichnan, R. H. 1972 Test-field model for inhomogeneous turbulence. J. Fluid Mech. 56, 287–304.CrossRefGoogle Scholar
Kraichnan, R. H. & Herring, J. R. 1978 A strain-based Lagrangian-history turbulence theory. J. Fluid Mech. 88, 355–367.Google Scholar
Launder, B. E., Reece, G. J. & Rodi, W. 1975 Progress in the development of a Reynolds-stress turbulent closure. J. Fluid Mech. 68, 537–566.Google Scholar
Lesieur, M. 2008 Turbulence in Fluids, 4th edn. Springer.Google Scholar
Leslie, D. C. 1973 Developments in the Theory of Turbulence. Clarendon.Google Scholar
Lumley, J. L. 1967 Similarity and the turbulent energy spectrum. Phys. Fluids 10 (4), 855–858.Google Scholar
Lumley, J. L.1975 Lectures Series, 76. Von Karman Institute.Google Scholar
Meyers, J. & Meneveau, C. 2008 A functional form of the energy spectrum parametrizing bottleneck and intermittency effects. Phys. Fluids 20, 065109.Google Scholar
Millionschikov, M. D. 1941 Theory of homogeneous isotropic turbulence. Dokl. Akad. Nauk SSSR 33, 22–24.Google Scholar
Mons, V., Meldi, M. & Sagaut, P. 2014 Numerical investigation on the partial return to isotropy of freely decaying homogeneous axisymmetric turbulence. Phys. Fluids 26, 025110.Google Scholar
O’Brien, E. F. & Francis, G. C. 1963 A consequence of the zero fourth cumulant approximation. J. Fluid Mech. 13, 369–382.CrossRefGoogle Scholar
Ogura, Y. 1963 A consequence of the zero fourth cumulant approximation in the decay of isotropic turbulence. J. Fluid Mech. 16, 33–40.CrossRefGoogle Scholar
Orszag, S. A. 1970 Analytical theories of turbulence. J. Fluid Mech. 41, 363–386.Google Scholar
Piquet, J. 2001 Turbulent Flows – Models and Physics, 2nd edn. Springer.Google Scholar
Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.CrossRefGoogle Scholar
Pouquet, A., Lesieur, M., André, J. C. & Basdevant, C. 1975 Evolution of high Reynolds number two-dimensional turbulence. J. Fluid Mech. 72, 305–319.Google Scholar
Proudman, I. & Reid, W. H. 1954 On the decay of a normally distributed and homogeneous turbulent velocity field. Phil. Trans. R. Soc. Lond. A 297, 163–189.Google Scholar
Rogers, M. M., Moin, P. & Reynolds, W. C.1986 The structure and modelling of the hydrodynamic and passive scalar fields in homogeneous shear turbulence. Report No. TF-25. Department of Mechanical Engineering, Stanford University, Stanford, CA.Google Scholar
Rohr, J. J., Itsweire, E. C., Helland, K. N. & Van Atta, C. W. 1988 An investigation of the growth of turbulence in a uniform-mean-shear flow. J. Fluid Mech. 187, 1–33.Google Scholar
Rubinstein, R. 1996 A relaxation approximation for time-dependent second-order effects in shear turbulence. Theor. Comput. Fluid Dyn. 8, 377–386.Google Scholar
Rubinstein, R., Kurien, S. & Cambon, C. 2015 Scalar and tensor spherical harmonics expansion of the velocity correlation in homogeneous anisotropic turbulence. J. Turbul. 16 (11), 1058–1075.Google Scholar
Sagaut, P. & Cambon, C. 2008 Homogeneous Turbulence Dynamics. Cambridge University Press.CrossRefGoogle Scholar
Schiestel, R. 1987 Multiple-time-scale modeling of turbulent flows in one-point closures. Phys. Fluids 30 (3), 722–731.Google Scholar
Shen, X. & Warhaft, Z. 2000 The anisotropy of the small scale structure in high Reynolds number $(R_{{\it\lambda}}\sim 1000)$ turbulent shear flow. Phys. Fluids 12, 2976–2989.Google Scholar
Speziale, C. G., Sarkar, S. & Gatski, T. B. 1991 Modelling the pressure–strain correlation of turbulence: an invariant dynamical systems approach. J. Fluid Mech. 227, 245–272.Google Scholar
Tavoularis, S. 1985 Asymptotic laws for transversely homogeneous turbulent shear flows. Phys. Fluids 28, 999–1001.Google Scholar
Tavoularis, S. & Corrsin, S. 1981 Experiments in nearly homogenous turbulent shear flow with a uniform mean temperature gradient. Part 1. J. Fluid Mech. 104, 311–347.Google Scholar
Tavoularis, S. & Karnik, U. 1989 Further experiments on the evolution of turbulent stresses and scales in uniformly sheared turbulence. J. Fluid Mech. 204, 457–478.Google Scholar
Townsend, A. A. 1976 The Structure of Turbulent Shear Flow, 2nd edn. Cambridge University Press.Google Scholar
Waleffe, F. 1992 The nature of triad interactions in homogeneous turbulence. Phys. Fluids 4, 350–363.CrossRefGoogle Scholar
Weinstock, J. 2013 Analytical theory of homogeneous mean shear turbulence. J. Fluid Mech. 727, 256–281.Google Scholar
Yoshida, K., Ishihara, T. & Kaneda, Y. 2003 Anisotropic spectrum of homogeneous turbulent shear flow in a Lagrangian renormalized approximation. Phys. Fluids 15 (8), 2385–2397.Google Scholar
Zhou, Y. 2010 Renormalization group theory for fluid and plasma turbulence. Phys. Rep. 488, 1–49.Google Scholar
Zusi, C. J. & Perot, J. B. 2013 Simulation and modeling of turbulence subjected to a period of uniform plane strain. Phys. Fluids 25, 110819.Google Scholar
Zusi, C. J. & Perot, J. B. 2014 Simulation and modeling of turbulence subjected to a period of axisymmetric contraction or expansion. Phys. Fluids 26, 115103.Google Scholar