Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-27T13:46:43.242Z Has data issue: false hasContentIssue false
  • English
  • Français

Spectral energy cascade in thermoacoustic shock waves

Published online by Cambridge University Press:  13 October 2017

Prateek Gupta Open the ORCID record for Prateek Gupta [Opens in a new window] ,
Guido Lodato  and
Carlo Scalo
Prateek Gupta*
Affiliation:
School of Mechanical Engineering, Purdue University, West Lafayette, IN 47906, USA
Guido Lodato
Affiliation:
Normandie Université, CNRS, INSA et Université de Rouen, CORIA UMR6614, France
Carlo Scalo
Affiliation:
School of Mechanical Engineering, Purdue University, West Lafayette, IN 47906, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We have investigated thermoacoustically amplified quasi-planar nonlinear waves driven to the limit of shock-wave formation in a variable-area looped resonator geometrically optimized to maximize the growth rate of the quasi-travelling-wave second harmonic. Optimal conditions result in velocity leading pressure by approximately $40^{\circ }$ in the thermoacoustic core and not in pure travelling-wave phasing. High-order unstructured fully compressible Navier–Stokes simulations reveal three regimes: (i) modal growth, governed by linear thermoacoustics; (ii) hierarchical spectral broadening, resulting in a nonlinear inertial energy cascade, (iii) shock-wave-dominated limit cycle, where energy production is balanced by dissipation occurring at the captured shock-thickness scale. The acoustic energy budgets in regime (i) have been analytically derived, yielding an expression of the Rayleigh index in closed form and elucidating the effect of geometry and hot-to-cold temperature ratio on growth rates. A time-domain nonlinear dynamical model is formulated for regime (ii), highlighting the role of second-order interactions between pressure and heat-release fluctuations, causing asymmetry in the thermoacoustic energy production cycle and growth rate saturation. Moreover, energy cascade is inviscid due to steepening in regime (ii), with the 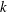$k$th harmonic growing at $k/2$-times the modal growth rate of the thermoacoustically sustained second harmonic. The frequency energy spectrum in regime (iii) is shown to scale with a 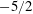$-5/2$ power law in the inertial range, rolling off at the captured shock-thickness scale in the dissipation range. We have thus shown the existence of equilibrium thermoacoustic energy cascade analogous to hydrodynamic turbulence.

JFM classification

Acoustics: Acoustics Nonlinear Dynamical Systems: Nonlinear Dynamical Systems Compressible Flows: Shock waves
Type
Papers
Information
Journal of Fluid Mechanics , Volume 831 , 25 November 2017 , pp. 358 - 393
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ananthkrishnan, N., Deo, S. & Culick, F. E. C. 2005 Reduced-order modeling and dynamics of nonlinear acoustic waves in a combustion chamber. Combust. Sci. Technol. 177 (2), 221–248.Google Scholar
Balasubramanian, K. & Sujith, R. I. 2008 Non-normality and nonlinearity in combustion–acoustic interaction in diffusion flames. J. Fluid Mech. 594, 29–57.Google Scholar
Biwa, T., Sobata, K., Otake, S. & Yazaki, T. 2014 Observation of thermoacoustic shock waves in a resonance tube. J. Acoust. Soc. Am. 136 (3), 965–968.CrossRefGoogle Scholar
Biwa, T., Takahashi, T. & Yazaki, T. 2011 Observation of traveling thermoacoustic shock waves (L). J. Acoust. Soc. Am. 130 (6), 3558–3561.Google Scholar
Chapelier, J.-B., Lodato, G. & Jameson, A. 2016 A study on the numerical dissipation of the spectral difference method for freely decaying and wall-bounded turbulence. Comput. Fluids 139, 261–280.CrossRefGoogle Scholar
Chester, W. 1964 Resonant oscillations in closed tubes. J. Fluid Mech. 18, 44–64.CrossRefGoogle Scholar
Chu, B. T. & Kovásznay, L. S. G. 1958 Non-linear interactions in a viscous heat-conducting compressible gas. J. Fluid Mech. 3 (05), 494.CrossRefGoogle Scholar
Culick, F. E. C. 1971 Non-linear growth and limiting amplitude of acoustic oscillations in combustion chambers. Combust. Sci. Technol. 3 (1), 1–16.Google Scholar
Culick, F. E. C.2006 Unsteady motions in combustion chambers for propulsion systems. Tech. Rep. RTO AGARDograph.Google Scholar
El-Rahman, A. I. A., Abdelfattah, W. A. & Fouad, M. A. 2017 A 3d investigation of thermoacoustic fields in a square stack. Intl J. Heat Mass Transfer 108, Part A, 292–300.Google Scholar
Gedeon, D. 1995 Sage: object-oriented software for cryocooler design. In Cryocoolers (ed. Ross, R. G. Jr.), vol. 8, pp. 281–292. Springer US.Google Scholar
Guedra, M. & Penelet, G. 2012 On the use of a complex frequency for the description of thermoacoustic engines. Acta Acust. United Ac. 98 (2), 232–241.Google Scholar
Gupta, P., Scalo, C. & Lodato, G. 2017 Numerical investigation and modeling of thermoacoustic shock waves. In 55th AIAA Aerospace Sciences Meeting. AIAA SciTech Forum, AIAA Paper 2017-0214.Google Scholar
Hamilton, M. F. & Blackstock, D. T.(Eds) 1998 Nonlinear Acoustics. Academic.Google Scholar
Hamilton, M. F., Ilinksii, Yu. A. & Zabolotskaya, E. A. 2002 Nonlinear two-dimensional model for thermoacoustic engines. J. Acoust. Soc. Am. 111 (5), 2076–2086.CrossRefGoogle ScholarPubMed
Harten, A. & Hyman, J. M. 1983 Self adjusting grid methods for one-dimensional hyperbolic conservation laws. J. Comput. Phys. 50 (2), 235–269.CrossRefGoogle Scholar
Hedberg, C. M. & Rudenko, O. V. 2011 Dissipative and hysteresis loops as images of irreversible processes in nonlinear acoustic fields. J. Appl. Phys. 110 (5), 053503.Google Scholar
Jameson, A. 2010 A proof of the stability of the spectral difference method for all orders of accuracy. J. Sci. Comput. 45 (1–3), 348–358.Google Scholar
Jameson, A. & Lodato, G. 2014 A note on the numerical dissipation from high-order discontinuous finite element schemes. Comput. Fluids 98, 186–195.Google Scholar
Karpov, S. & Prosperetti, A. 2000 Nonlinear saturation of the thermoacoustic instability. J. Acoust. Soc. Am. 107 (6), 3130–3147.Google Scholar
Kolmogorov, A. N. 1941 The local structure of turbulence in incompressible viscous fluid for very large Reynolds numbers. Dokl. Akad. Nauk SSSR 30 (4), 299–303.Google Scholar
Kopriva, D. A. 1996 A conservative staggered-grid Chebyshev multidomain method for compressible flows. II. A semi-structured method. J. Comput. Phys. 128 (2), 475–488.Google Scholar
Kopriva, D. A. & Kolias, J. H. 1996 A conservative staggered-grid Chebyshev multidomain method for compressible flows. J. Comput. Phys. 125 (1), 244–261.Google Scholar
Lin, J., Scalo, C. & Hesselink, L. 2016 High-fidelity simulation of a standing-wave thermoacoustic–piezoelectric engine. J. Fluid Mech. 808, 19–60.Google Scholar
Lodato, G., Castonguay, P. & Jameson, A. 2013 Discrete filter operators for Large–Eddy simulation using high-order spectral difference methods. Intl J. Numer. Meth. Fluids 72 (2), 231–258.Google Scholar
Lodato, G., Castonguay, P. & Jameson, A. 2014 Structural wall-modeled LES using a high-order spectral difference scheme for unstructured meshes. Flow Turbul. Combust. 92 (1–2), 579–606.Google Scholar
Lodato, G., Vervisch, L. & Clavin, P. 2016 Direct numerical simulation of shock wavy-wall interaction: analysis of cellular shock structures and flow patterns. J. Fluid Mech. 789, 221–258.Google Scholar
Lodato, G., Vervisch, L. & Clavin, P. 2017 Numerical study of smoothly perturbed shocks in the Newtonian limit. Flow Turbul. Combust. (in press).Google Scholar
Menguy, L. & Gilbert, J. 2000 Weakly nonlinear gas oscillations in air-filled tubes; solutions and experiments. Acta Acust. United Ac. 86 (5), 798–810.Google Scholar
Naugol’Nykh, K. A. & Rybak, S. A. 1975 Spectrum of acoustic turbulence. Zh. Eksp. Teor. Fiz. 68, 78–84.Google Scholar
Nazarenko, S. 2011 Wave Turbulence. Springer Science & Business Media.Google Scholar
Olivier, C., Penelet, G., Poignand, G., Gilbert, J. & Lotton, P. 2015 Weakly nonlinear propagation in thermoacoustic engines: a numerical study of higher harmonics generation up to the appearance of shock waves. Acta Acust. United Ac. 101 (5), 941–949.CrossRefGoogle Scholar
Penelet, G., Gusev, V., Lotton, P. & Bruneau, M. 2005 Experimental and theoretical study of processes leading to steady-state sound in annular thermoacoustic engines. Phys. Rev. E 72, 016625.Google Scholar
Persson, P. O. & Peraire, J.2006 Sub-cell shock capturing for discontinuous Galerkin methods. AIAA Paper 2006-112, 1–13.Google Scholar
Pierce, A. D. 1989 Acoustics: An Introduction to its Physical Principles and Applications. Acoustical Society of America.Google Scholar
Poinsot, T. & Veynante, D. 2011 Theoretical and Numerical Combustion, 3rd edn. R. T. Edwards, Inc.Google Scholar
Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.Google Scholar
Rayleigh, Lord 1878 The explanation of certain acoustical phenomena. Nature 18, 319–321.Google Scholar
Roe, P. L. 1981 Approximate riemann solvers, parameter vectors, and difference schemes. J. Comput. Phys. 43 (2), 357–372.Google Scholar
Rott, N. 1969 Damped and thermally driven acoustic oscillations in wide and narrow tubes. Z. Angew. Math. Phys. 20, 230–243.CrossRefGoogle Scholar
Rott, N. 1973 Thermally driven acoustic oscillations, part II: stability limit for helium. Z. Angew. Math. Phys. 24, 54–72.Google Scholar
Saenger, R. A. & Hudson, G. E. 1960 Periodic shock waves in resonating gas columns. J. Acoust. Soc. Am. 32 (8), 961–970.Google Scholar
Sugimoto, N. 2010 Thermoacoustic-wave equations for gas in a channel and a tube subject to temperature gradient. J. Fluid Mech. 658, 89–116.Google Scholar
Sugimoto, N. 2016 Nonlinear theory for thermoacoustic waves in a narrow channel and pore subject to a temperature gradient. J. Fluid Mech. 797, 765–801.Google Scholar
Sun, Y., Wang, Z. J. & Liu, Y. 2007 High-order multidomain spectral difference method for the Navier–Stokes equations on unstructured hexahedral grids. Commun. Comput. Phys. 2 (2), 310–333.Google Scholar
Swift, G. W. 1988 Thermoacoustic engines. J. Acoust. Soc. Am. 84 (4), 1145–1181.Google Scholar
Swift, G. W. 1992 Analysis and performance of a large thermoacoustic engine. J. Acoust. Soc. Am. 92 (3), 1551–1563.Google Scholar
Yazaki, T., Iwata, A., Maekawa, T. & Tominaga, A. 1998 Traveling wave thermoacoustic engine in a looped tube. Phys. Rev. Lett. 81 (15), 3128–3131.Google Scholar
Zakharov, V. E., L’vov, V. S. & Falkovich, G. 2012 Kolmogorov Spectra of Turbulence I: Wave Turbulence. Springer Science & Business Media.Google Scholar

Gupta et al. supplementary movie

Growth of spectral energy extracted from the pressure signal shown in figure 5. The corresponding acoustic energy density evolution is shown in figure 14.

Download Gupta et al. supplementary movie(Video)
Video 5.8 MB