Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-26T18:29:40.589Z Has data issue: false hasContentIssue false
  • English
  • Français

Spatially varying mixing of a passive scalar in a buoyancy-driven turbulent flow

Published online by Cambridge University Press:  24 February 2014

Daan D. J. A. van Sommeren ,
C. P. Caulfield  and
Andrew W. Woods
Daan D. J. A. van Sommeren
Affiliation:
BP Institute, University of Cambridge, Madingley Road, Cambridge CB3 0EZ, UK Department of Applied Mathematics and Theoretical Physics, Centre for Mathematical Sciences, University of Cambridge, Wilberforce Road, Cambridge CB3 0WA, UK
C. P. Caulfield*
Affiliation:
BP Institute, University of Cambridge, Madingley Road, Cambridge CB3 0EZ, UK Department of Applied Mathematics and Theoretical Physics, Centre for Mathematical Sciences, University of Cambridge, Wilberforce Road, Cambridge CB3 0WA, UK
Andrew W. Woods
Affiliation:
BP Institute, University of Cambridge, Madingley Road, Cambridge CB3 0EZ, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We perform experiments to study the mixing of passive scalar by a buoyancy-induced turbulent flow in a long narrow vertical tank. The turbulent flow is associated with the downward mixing of a small flux of dense aqueous saline solution into a relatively large upward flux of fresh water. In steady state, the mixing region is of finite extent, and the intensity of the buoyancy-driven mixing is described by a spatially varying turbulent diffusion coefficient 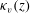$\kappa _v(z)$ which decreases linearly with distance $z$ from the top of the tank. We release a pulse of passive scalar into either the fresh water at the base of the tank, or the saline solution at the top of the tank, and we measure the subsequent mixing of the passive scalar by the flow using image analysis. In both cases, the mixing of the passive scalar (the dye) is well-described by an advection–diffusion equation, using the same turbulent diffusion coefficient 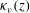$\kappa _v(z)$ associated with the buoyancy-driven mixing of the dynamic scalar. Using this advection–diffusion equation with spatially varying turbulent diffusion coefficient 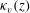$\kappa _v(z)$, we calculate the residence time distribution (RTD) of a unit mass of passive scalar released as a pulse at the bottom of the tank. The variance in this RTD is equivalent to that produced by a uniform eddy diffusion coefficient with value 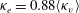$\kappa _e= 0.88 \langle \kappa _v \rangle $, where 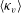$\langle \kappa _v \rangle $ is the vertically averaged eddy diffusivity. The structure of the RTD is also qualitatively different from that produced by a flow with uniform eddy diffusion coefficient. The RTD using 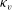$\kappa _v$ has a larger peak value and smaller values at early times, associated with the reduced diffusivity at the bottom of the tank, and manifested mathematically by a skewness 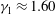$\gamma _1\approx 1.60$ and an excess kurtosis 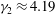$\gamma _2\approx 4.19 $ compared to the skewness and excess kurtosis of 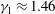$\gamma _1\approx 1.46$, 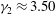$\gamma _2 \approx 3.50$ of the RTD produced by a constant eddy diffusion coefficient with the same variance.

JFM classification

Mixing: Turbulent mixing Turbulent Flows: Turbulent Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 742 , 10 March 2014 , pp. 701 - 719
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Baird, M. H. I., Aravamudan, K., Rao, N. V. R., Chadam, J. & Peirce, A. P. 1992 Unsteady axial mixing by natural convection in a vertical column. AIChE J. 38, 1825–1834.CrossRefGoogle Scholar
Boffetta, G., Lillo, F. D., Mazzino, A. & Musacchio, S. 2012 Bolgiano scale in confined Rayleigh–Taylor turbulence. J. Fluid Mech. 690, 426–440.CrossRefGoogle Scholar
Crimaldi, J. P. 2008 Planar laser induced fluorescence in aqueous flows. Exp. Fluids 44, 851–863.CrossRefGoogle Scholar
Dalziel, S. B., Patterson, M. D., Caulfield, C. P. & Coomaraswamy, I. A. 2008 Mixing efficiency in high-aspect-ratio Rayleigh–Taylor experiments. Phys. Fluids 20, 065106.CrossRefGoogle Scholar
Danckwerts, P. 1953 Continuous flow systems: Distribution of residence times. Chem. Engng Sci. 2, 1–13.CrossRefGoogle Scholar
Debacq, M., Fanguet, V., Hulin, J. P., Salin, D. & Perrin, B. 2001 Self-similar concentration profiles in buoyant mixing of miscible fluids in a vertical tube. Phys. Fluids 13, 3097–3100.CrossRefGoogle Scholar
Fragoso, A. T., Patterson, M. D. & Wettlaufer, J. S. 2013 Mixing in gravity currents. J. Fluid Mech. 734, R2, 10 pages.CrossRefGoogle Scholar
van der Laan, E. T. 1958 Notes on the diffusion-type model for the longitudinal mixing in flow. Chem. Engng Sci. 7, 187–191.Google Scholar
Levenspiel, O. 1999 Chemical Reaction Engineering. John Wiley and Sons.Google Scholar
MacMullin, R. & Weber, M. 1935 The theory of short-circuiting in continuous-flow mixing vessels in series and kinetics of chemical reactions in such systems. Trans. Am. Inst. Chem. Engng 31, 409–458.Google Scholar
Mashayek, A., Caulfield, C. P. & Peltier, W. R. 2013 Time-dependent, non-monotonic mixing in stratified turbulent shear flows: implications for oceanographic estimates of buoyancy flux. J. Fluid Mech. 736, 570–593.CrossRefGoogle Scholar
Nauman, E. B. 2004 Residence Time Distributions. Handbook of Industrial Mixing: Science and Practice. Wiley Interscience.Google Scholar
Prandtl, L. 1925 A report on testing for built-up turbulence. Z. Angew. Math. Mech. 5, 136–139.CrossRefGoogle Scholar
van Sommeren, D. D. J. A., Caulfield, C. P. & Woods, A. W. 2012 Turbulent buoyant convection from a maintained source of buoyancy in a narrow vertical tank. J. Fluid Mech. 701, 278–303 (Herein referred to as VS12.).CrossRefGoogle Scholar
van Sommeren, D. D. J. A., Caulfield, C. P. & Woods, A. W. 2013 Advection and buoyancy-induced turbulent diffusion in a narrow vertical tank. J. Fluid Mech. 724, 450–479 (Herein referred to as VS13.).CrossRefGoogle Scholar
Troy, C. D. & Koseff, J. R. 2008 The generation and quantitative visualization of breaking internal waves. Exp. Fluids 38, 549–562.CrossRefGoogle Scholar
Xu, D. & Chen, J. 2012 Experimental study of stratified jet by simultaneous measurements of velocity and density fields. Exp. Fluids 53, 145–162.CrossRefGoogle Scholar