Published online by Cambridge University Press: 21 May 2024
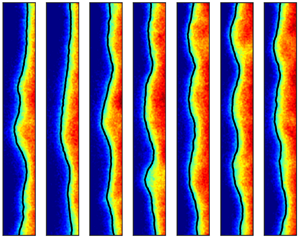
Three-dimensional effects of sidewalls on the low-frequency unsteadiness of the shock-wave/boundary-layer interaction (SBLI) are of academic and practical importance but not yet well understood. Considerable attention has been paid to the viscous effect of sidewalls, whereas the potential inviscid confinement effect of sidewalls has received little attention. The present work provides experimental evidence of multiscale spanwise travelling waves crossing the separation front under the confinement of sidewalls. Global pressure measurements were made for a sidewall-confined 24 $^\circ$ compression ramp interaction in Mach-2.83 flow using fast-responding pressure-sensitive paint. The unsteady pressure in a statistically two-dimensional intermittent region suggests that in addition to the canonical streamwise oscillation, the separation front exhibits significant low-frequency, multiscale spanwise distortion. Modal analysis further reveals that multiscale spanwise unsteadiness has higher intensity and frequency than the streamwise oscillation. Such strong spanwise unsteadiness calls attention to the low-frequency unsteadiness in previous sidewall-confined SBLI experiments and encourages further study on the mechanism of the confinement effect.
$^\circ$ compression ramp interaction in Mach-2.83 flow using fast-responding pressure-sensitive paint. The unsteady pressure in a statistically two-dimensional intermittent region suggests that in addition to the canonical streamwise oscillation, the separation front exhibits significant low-frequency, multiscale spanwise distortion. Modal analysis further reveals that multiscale spanwise unsteadiness has higher intensity and frequency than the streamwise oscillation. Such strong spanwise unsteadiness calls attention to the low-frequency unsteadiness in previous sidewall-confined SBLI experiments and encourages further study on the mechanism of the confinement effect.