Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-04T19:39:06.694Z Has data issue: false hasContentIssue false
  • English
  • Français

Space–time pressure–velocity correlations in a turbulent boundary layer

Published online by Cambridge University Press:  22 April 2015

Yoshitsugu Naka ,
Michel Stanislas ,
Jean-Marc Foucaut ,
Sebastien Coudert ,
Jean-Philippe Laval  and
Shinnosuke Obi
Yoshitsugu Naka
Affiliation:
Ecole Centrale de Lille, Université Lille Nord de France, Laboratoire de Mécanique de Lille, Boulevard Paul Langevin, 59655 Villeneuve d’Ascq, France
Michel Stanislas
Affiliation:
Ecole Centrale de Lille, Université Lille Nord de France, Laboratoire de Mécanique de Lille, Boulevard Paul Langevin, 59655 Villeneuve d’Ascq, France
Jean-Marc Foucaut
Affiliation:
Ecole Centrale de Lille, Université Lille Nord de France, Laboratoire de Mécanique de Lille, Boulevard Paul Langevin, 59655 Villeneuve d’Ascq, France
Sebastien Coudert
Affiliation:
CNRS, Université Lille Nord de France, Laboratoire de Mécanique de Lille, Boulevard Paul Langevin, 59655 Villeneuve d’Ascq, France
Jean-Philippe Laval
Affiliation:
CNRS, Université Lille Nord de France, Laboratoire de Mécanique de Lille, Boulevard Paul Langevin, 59655 Villeneuve d’Ascq, France
Shinnosuke Obi
Affiliation:
Department of Mechanical Engineering, Keio University, 3-14-1 Hiyoshi, Kohoku-ku, Yokohama 223-8522, Japan
Get access Rights & Permissions [Opens in a new window]

Abstract

The spatio-temporal pressure–velocity correlation in a turbulent boundary layer is investigated so as to understand the link between pressure fluctuations and turbulent coherent structures. A new experimental set-up is developed to measure the pressure fluctuations at the wall and in the field and, simultaneously, the velocity field by stereoscopic particle image velocimetry. The present measurement area covers the whole boundary layer thickness, and the spatial resolution of the measurement is good enough to assess the representative length scales of the flow. The Reynolds number effect is quantified from the data at 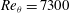$\mathit{Re}_{{\it\theta}}=7300$, 10 000, 18 000. The spatio-temporal three-dimensional structures of the pressure–velocity correlations, 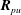$\boldsymbol{R}_{pu}$, 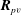$\boldsymbol{R}_{pv}$ and 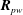$\boldsymbol{R}_{pw}$, are evaluated. The wall pressure fluctuations are closely coupled with coherent structures which occupy a large region of the boundary layer in the wall-normal and spanwise directions and up to 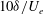$10{\it\delta}/U_{e}$ in time, where 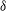${\it\delta}$ and 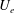$U_{e}$ denote the boundary layer thickness and the free stream velocity. Reynolds number effects are mainly observed on the size and intensity of the pressure–velocity correlations. Conditioning the correlations on the pressure signal sign shows different types of flow phenomena linked to the positive and negative pressure events. For the wall pressure, positive pressure fluctuations appear to be correlated with the leading edge of a large sweeping motion of splatting type followed by a large ejection. The negative pressure fluctuations are linked to a localized ejection upstream, followed by a large sweeping motion downstream. For the pressure fluctuations in the field, in addition to the structures observed with the wall pressure, the pressure–velocity correlations exhibit a significant correlation in a region very extended in time. Such long structures appear to be independent of the one observed at the wall and to grow significantly in time with the Reynolds number when scaling with external variables. When conditioned by the pressure sign, clear ejection and sweeping motions are observed with associated streamwise vortical structures at a scale of the order of 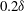$0.2{\it\delta}$. These structures can be linked to the large-scale motion and very-large-scale motion previously observed by different authors and seem to organize in a scheme analogous to the near-wall cycle, but at a much larger scale.

JFM classification

Boundary Layers: Boundary layer structure Turbulent Flows: Turbulent boundary layers
Type
Papers
Information
Journal of Fluid Mechanics , Volume 771 , 25 May 2015 , pp. 624 - 675
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adrian, R. J. 2007 Hairpin vortex organization in wall turbulence. Phys. Fluids 19 (4), 041301.CrossRefGoogle Scholar
Adrian, R. J., Meinhart, C. D. & Tomkins, C. D. 2000 Vortex organization in the outer region of the turbulent boundary layer. J. Fluid Mech. 422, 1–54.Google Scholar
Blackwelder, R. F. & Kaplan, R. E. 1976 On the wall structure of the turbulent boundary layer. J. Fluid Mech. 76 (01), 89–112.CrossRefGoogle Scholar
Blake, W. K. 1970 Turbulent boundary layer wall pressure fluctuations on smooth and rough wall. J. Fluid Mech. 44, 637–660.CrossRefGoogle Scholar
Bradshaw, P. 1967 Inactive motion and pressure fluctuations in turbulent boundary layers. J. Fluid Mech. 30, 241–258.CrossRefGoogle Scholar
Bull, M. K. 1967 Wall-pressure fluctuations associated with subsonic turbulent boundary layer flow. J. Fluid Mech. 28, 719–754.Google Scholar
Bull, M. K. 1996 Wall pressure fluctuations beneath turbulent boundary layers: some reflections on forty years of research. J. Sound Vib. 190, 299–315.Google Scholar
Carlier, J. & Stanislas, M. 2005 Experimental study of eddy structures in a turbulent boundary layer using particle image velocimetry. J. Fluid Mech. 535, 143–188.CrossRefGoogle Scholar
Chang, P. A., Piomelli, U. & Blake, W. K. 1999 Relationship between wall pressure and velocity-field sources. Phys. Fluids 11 (11), 3434–3448.CrossRefGoogle Scholar
Christensen, K. T. & Adrian, R. J. 2001 Statistical evidence of hairpin vortex packets in wall turbulence. J. Fluid Mech. 431, 433–443.Google Scholar
Corcos, G. M. 1963 The structure of the turbulent pressure field in boundary-layer flows. J. Fluid Mech. 18, 353–378.CrossRefGoogle Scholar
Coudert, S. & Schon, J. P. 2001 Back projection algorithm with misalignment corrections for 2D3C stereoscopic PIV. Meas. Sci. Technol. 12, 1371–1381.CrossRefGoogle Scholar
Del Álamo, J. C., Jiménez, J., Zandonade, P. & Moser, R. D. 2004 Scaling of the energy spectra of turbulent channels. J. Fluid Mech. 500, 135–144.Google Scholar
Eckelman, H. 1989 A review of knowledge on pressure fluctuations. In Near-Wall Turbulence, pp. 328–347.Google Scholar
Elliot, J. A. 1972 Microscale pressure fluctuations measured within the lower atmospheric boundary layer. J. Fluid Mech. 53, 351–383.CrossRefGoogle Scholar
Falco, R. E. 1991 A coherent structure model of the turbulent boundary layer and its ability to predict Reynolds number dependence. Phil. Trans. R. Soc. Lond. A 336 (1641), 103–129.Google Scholar
Farabee, T. M. & Casarella, M. J. 1991 Spectral features of wall pressure fluctuations beneath turbulent boundary layers. Phys. Fluids 3 (10), 2410–2420.Google Scholar
Foucaut, J.-M., Coudert, S., Stanislas, M. & Delville, J. 2011 Full 3D correlation tensor computed from double field stereoscopic PIV in a high Reynolds number turbulent boundary layer. Exp. Fluids 50, 839–846.Google Scholar
Foucaut, J.-M., Kostas, J. & Stanislas, M.2006 Wall shear stress measurement using stereoscopic PIV. In 12th International Symposium on Flow Visualization pp. 249–258.Google Scholar
Ganapathisubramani, B., Clemens, N. T. & Dolling, D. S. 2006 Large-scale motions in a supersonic turbulent boundary layer. J. Fluid Mech. 556, 271–282.Google Scholar
Ghaemi, S. & Scarano, F. 2013 Turbulent structure of high-amplitude pressure peaks within the turbulent boundary layer. J. Fluid Mech. 735, 381–426.Google Scholar
Gravante, S. P., Naguib, A. M., Wark, C. E. & Nagib, H. M. 1998 Characterization of the pressure fluctuations under a fully developed turbulent boundary layer. AIAA J. 36, 1808–1816.CrossRefGoogle Scholar
Herpin, S., Stanislas, M., Foucaut, J.-M. & Coudert, S. 2013 Influence of the Reynolds number on the vortical structures in the logarithmic region of turbulent boundary layers. J. Fluid Mech. 716, 5–50.Google Scholar
Heyes, M. H. 1996 Statistical Digital Signal Processing and Modeling. John Wiley & Sons.Google Scholar
Hultmark, M., Vallikivi, M., Bailey, S. C. C. & Smits, A. J. 2013 Logarithmic scaling of turbulence in smooth- and rough-wall pipe flow. J. Fluid Mech. 728, 376–395.Google Scholar
Hutchins, N. & Marusic, I. 2007 Evidence of very long meandering features in the logarithmic region of turbulent boundary layers. J. Fluid Mech. 579, 1–28.CrossRefGoogle Scholar
Jiménez, J. 2012 Cascades in wall-bounded turbulence. Annu. Rev. Fluid Mech. 44 (1), 27–45.Google Scholar
Jiménez, J. 2013 Near-wall turbulence. Phys. Fluids 25 (10), 101302.Google Scholar
Johansson, A. V., Her, J.-Y. & Haritonidis, J. H. 1987 On the generation of high-amplitude wall-pressure peaks in turbulent boundary layers and spots. J. Fluid Mech. 175, 119–142.Google Scholar
de Kat, R. & van Oudheusden, B. W. 2012 Instantaneous planar pressure determination from PIV in turbulent flow. Exp. Fluids 52 (5), 1089–1106.CrossRefGoogle Scholar
Kawata, T., Naka, Y. & Obi, S. 2014 Simultaneous measurement of fluctuating velocity and pressure in the near wake of a circular cylinder. Exp. Fluids 55 (5), 1–12.CrossRefGoogle Scholar
Kim, J. 1983 On the structure of wall bounded turbulent flows. Phys. Fluids 26, 2088–2097.Google Scholar
Kim, J. 1989 On the structure of pressure fluctuations in simulated turbulent channel flow. J. Fluid Mech. 205, 421–451.CrossRefGoogle Scholar
Klewicki, J. C., Priyadarshana, P. J. A. & Metzger, M. M. 2008 Statistical structure of the fluctuating wall pressure and its in-plane gradients at high Reynolds number. J. Fluid Mech. 609, 195–220.CrossRefGoogle Scholar
Kobashi, Y. & Ichijo, M. 1986 Wall pressure and its relation to turbulent structure of a boundary layer. Exp. Fluids 4 (1), 49–55.CrossRefGoogle Scholar
Kobashi, Y., Komoda, H. & Ichijo, M. 1984 Wall pressure fluctuation and the turbulence structure of a boundary layer. In Turbulence and Chaotic Phenomena in Fluids, pp. 461–466.Google Scholar
Kovasznay, L. S. G., Kibens, V. & Blackwelder, R. F. 1970 Large-scale motion in the intermittent region of a turbulent boundary layer. J. Fluid Mech. 41, 283–325.Google Scholar
Lin, J., Foucaut, J.-M., Laval, J.-P., Pérenne, N. & Stanislas, M. 2008 Assessment of different SPIV processing methods for an application to near-wall turbulence. In Particle Image Velocimetry, Topics in Applied Physics, vol. 112, pp. 191–221. Springer.Google Scholar
Liu, X. & Katz, J. 2006 Instantaneous pressure and material acceleration measurements using a four-exposure PIV system. Exp. Fluids 41 (2), 227–240.Google Scholar
Marusic, I. & Kunkel, G. J. 2003 Streamwise turbulence intensity formulation for flat-plate boundary layers. Phys. Fluids 15 (8), 2461–2464.Google Scholar
Marusic, I., Mathis, R. & Hutchins, N. 2010 Predictive model for wall-bounded turbulent flow. Science 329, 193–196.Google Scholar
Mathis, R., Hutchins, N. & Marusic, I. 2009 Large-scale amplitude modulation of the small-scale structures in turbulent boundary layers. J. Fluid Mech. 628, 311–337.CrossRefGoogle Scholar
Mathis, R., Hutchins, N. & Marusic, I. 2011 A predictive inner–outer model for streamwise turbulence statistics in wall-bounded flows. J. Fluid Mech. 681, 537–566.Google Scholar
Morrison, J. F. 2007 The interaction between inner and outer regions of turbulent wall-bounded flow. Phil. Trans. R. Soc. Lond. A 365, 683–698.Google Scholar
Naguib, A. M., Wark, C. E. & Juckenhöfel, O. 2001 Stochastic estimation and flow sources associated with surface pressure events in a turbulent boundary layer. Phys. Fluids 13 (9), 2611–2626.CrossRefGoogle Scholar
Naka, Y.2009 Simultaneous measurement of fluctuating velocity and pressure in turbulent free shear flows. PhD thesis, Keio University.Google Scholar
Naka, Y., Omori, T., Obi, S. & Masuda, S. 2006 Simultaneous measurement of fluctuating velocity and pressure in a turbulent mixing layer. Intl J. Heat Fluid Flow 737–746, 27.Google Scholar
Panton, R. L. 2001 Overview of the self-sustaining mechanisms of wall turbulence. Prog. Aerosp. Sci. 37 (4), 341–383.Google Scholar
Schewe, G. 1983 On the structure and resolution of wall-pressure fluctuations associated with turbulent boundary-layer flow. J. Fluid Mech. 134, 311–328.CrossRefGoogle Scholar
Schlatter, P. & Örlü, R. 2010 Assessment of direct numerical simulation data of turbulent boundary layers. J. Fluid Mech. 659, 116–126.Google Scholar
Schoppa, W. & Hussain, F. 2002 Coherent structure generation in near-wall turbulence. J. Fluid Mech. 453, 57–108.Google Scholar
Smits, A. J., Mckeon, B. J. & Marusic, I. 2011 High-Reynolds number wall turbulence. Annu. Rev. Fluid Mech. 43, 353–375.Google Scholar
Soloff, S., Adrian, R. J. & Liu, Z.-C. 1997 Distortion compensation for generalized stereoscopic particle image velocimetry. Meas. Sci. Technol. 8, 1441–1454.Google Scholar
Stanislas, M., Perret, L. & Foucaut, J.-M. 2008 Vortical structures in the turbulent boundary layer: a possible route to a universal representation. J. Fluid Mech. 602, 327–382.Google Scholar
Tanahashi, M., Kang, S.-J., Miyamoto, T., Shiokawa, S. & Miyauchi, T. 2004 Scaling law of fine scale eddies in turbulent channel flows up to $\mathit{Re}_{{\it\tau}}=800$ . Intl J. Heat Fluid Flow 25, 331–340.Google Scholar
Thomas, A. S. W. & Bull, M. K. 1983 On the role of wall-pressure fluctuations in deterministic motions in the turbulent boundary layer. J. Fluid Mech. 128, 283–322.CrossRefGoogle Scholar
Tomkins, C. D. & Adrian, R. J. 2003 Spanwise structure and scale growth in turbulent boundary layers. J. Fluid Mech. 490, 37–74.Google Scholar
Toyoda, K., Okamoto, T. & Shirahama, Y. 1994 Eduction of vortical structures by pressure measurements in noncircular jets. Appl. Sci. Res. 53, 237–248.Google Scholar
Tritton, D. J. 1967 Some new correlation measurements in a turbulent boundary layer. J. Fluid Mech. 28, 439–462.Google Scholar
Tsuji, Y., Fransson, J. H. M., Alfredsson, P. H. & Johansson, A. V. 2007 Pressure statistics and their scaling in high-Reynolds-number turbulent boundary layers. J. Fluid Mech. 585, 1–40.Google Scholar
Tsuji, Y., Imayama, S., Schlatter, P., Alfredsson, P. H., Johansson, A. V., Marusic, I., Hutchins, N. & Monty, J. 2012 Pressure fluctuation in high-Reynolds-number turbulent boundary layer: results from experiments and DNS. J. Turbul. 13 (N50).CrossRefGoogle Scholar
Tsuji, Y. & Ishihara, T. 2003 Similarity scaling of pressure fluctuation in turbulence. Phys. Rev. E 68, 026309.Google Scholar
Tutkun, M., George, W. K., Delville, J., Stanislas, M., Johansson, P. B. V., Foucaut, J.-M. & Coudert, S. 2009 Two-point correlations in high Reynolds number flat plate turbulent boundary layers. J. Turbul. 10 (N21).Google Scholar
van Oudheusden, B. W., Scarano, F., Roosenboom, E. W. M., Casimiri, E. W. F. & Souverein, L. J. 2007 Evaluation of integral forces and pressure fields from planar velocimetry data for incompressible and compressible flows. Exp. Fluids 43 (2–3), 153–162.CrossRefGoogle Scholar
Willert, C. 1997 Stereoscopic digital image velocimetry for applications in wind tunnel flows. Meas. Sci. Technol. 8, 1465–1479.CrossRefGoogle Scholar
Willmarth, W. W. 1975 Pressure fluctuations beneath turbulent boundary layers. Annu. Rev. Fluid Mech. 7, 13–36.Google Scholar
Willmarth, W. W. & Wooldridge, C. E. 1963 Measurements of the correlation between the fluctuating velocities and fluctuating wall pressure in a thick turbulent boundary layer. AGARD Rep. (456).Google Scholar

Naka et al. supplementary movie

3D view of conditional wall pressure-streamwise velocity correlation Rpu for p>0 at Re_Į=10 000. The movie shows the 3D structure of the correlation as follows: 1. oblique view of positive and negative isosurfaces; 2. cut in Ģt-y plane scanning through spanwise locations; 3. cut in y-z plane at Ģt=0; 4. changing the values of isosurfaces; 5. showing the isosurfaces in different angles.

Download Naka et al. supplementary movie(Video)
Video 5.4 MB

Naka et al. supplementary movie

3D view of conditional wall pressure-streamwise velocity correlation Rpu for p>0 at Re_Į=10 000. The movie shows the 3D structure of the correlation as follows: 1. oblique view of positive and negative isosurfaces; 2. cut in Ģt-y plane scanning through spanwise locations; 3. cut in y-z plane at Ģt=0; 4. changing the values of isosurfaces; 5. showing the isosurfaces in different angles.

Download Naka et al. supplementary movie(Video)
Video 12.9 MB

Naka et al. supplementary movie

3D view of conditional wall pressure-streamwise velocity correlation Rpu for p<0 at Re_Į=10 000. The representation is the same as movie 1.

Download Naka et al. supplementary movie(Video)
Video 5.1 MB

Naka et al. supplementary movie

3D view of conditional wall pressure-streamwise velocity correlation Rpu for p<0 at Re_Į=10 000. The representation is the same as movie 1.

Download Naka et al. supplementary movie(Video)
Video 12 MB

Naka et al. supplementary movie

3D view of conditional wall pressure-wall normal velocity correlation Rpv for p>0 at Re_Į=10 000. The representation is the same as movie 1.

Download Naka et al. supplementary movie(Video)
Video 5.1 MB

Naka et al. supplementary movie

3D view of conditional wall pressure-wall normal velocity correlation Rpv for p>0 at Re_Į=10 000. The representation is the same as movie 1.

Download Naka et al. supplementary movie(Video)
Video 12.1 MB

Naka et al. supplementary movie

3D view of conditional wall pressure-wall normal velocity correlation Rpv for p<0 at Re_Į=10 000. The representation is the same as movie 1.

Download Naka et al. supplementary movie(Video)
Video 5 MB

Naka et al. supplementary movie

3D view of conditional wall pressure-wall normal velocity correlation Rpv for p<0 at Re_Į=10 000. The representation is the same as movie 1.

Download Naka et al. supplementary movie(Video)
Video 12 MB

Naka et al. supplementary movie

3D view of conditional wall pressure-spanwise velocity correlation Rpw for p>0 at Re_Į=10 000. The representation is the same as movie 1.

Download Naka et al. supplementary movie(Video)
Video 5.2 MB

Naka et al. supplementary movie

3D view of conditional wall pressure-spanwise velocity correlation Rpw for p>0 at Re_Į=10 000. The representation is the same as movie 1.

Download Naka et al. supplementary movie(Video)
Video 12.6 MB

Naka et al. supplementary movie

3D view of conditional wall pressure-spanwise velocity correlation Rpw for p<0 at Re_Į=10 000. The representation is the same as movie 1.

Download Naka et al. supplementary movie(Video)
Video 5.4 MB

Naka et al. supplementary movie

3D view of conditional wall pressure-spanwise velocity correlation Rpw for p<0 at Re_Į=10 000. The representation is the same as movie 1.

Download Naka et al. supplementary movie(Video)
Video 13.1 MB

Naka et al. supplementary movie

Three components of conditional wall pressure-velocity correlations represented by color (Rpu) and vectors (Rpv and Rpw) for p>0 at Re_ƒÆ=10 000. Distribution in $y-z$ plane is scanned within -1.5 < ƒ¢tUe/ƒÂ < 1.

Download Naka et al. supplementary movie(Video)
Video 10.3 MB

Naka et al. supplementary movie

Three components of conditional wall pressure-velocity correlations represented by color (Rpu) and vectors (Rpv and Rpw) for p>0 at Re_ƒÆ=10 000. Distribution in $y-z$ plane is scanned within -1.5 < ƒ¢tUe/ƒÂ < 1.

Download Naka et al. supplementary movie(Video)
Video 30.5 MB

Naka et al. supplementary movie

Three components of conditional wall pressure-velocity correlations represented by color (Rpu) and vectors (Rpv and Rpw) for p<0 at Re_ƒÆ=10 000. Distribution in y-z plane is scanned within -1 < ƒ¢tUe/ƒÂ < 1.5.

Download Naka et al. supplementary movie(Video)
Video 10.2 MB

Naka et al. supplementary movie

Three components of conditional wall pressure-velocity correlations represented by color (Rpu) and vectors (Rpv and Rpw) for p<0 at Re_ƒÆ=10 000. Distribution in y-z plane is scanned within -1 < ƒ¢tUe/ƒÂ < 1.5.

Download Naka et al. supplementary movie(Video)
Video 34 MB

Naka et al. supplementary movie

3D view of field pressure-streamwise velocity correlation Rpu at probe position (b: yp+=48) at Re_ƒÆ=10 000. The correlation is Gaussian filtered with a width of ƒÐ+=18.9. The representation is the same as movie 1.

Download Naka et al. supplementary movie(Video)
Video 3.9 MB

Naka et al. supplementary movie

3D view of field pressure-streamwise velocity correlation Rpu at probe position (b: yp+=48) at Re_ƒÆ=10 000. The correlation is Gaussian filtered with a width of ƒÐ+=18.9. The representation is the same as movie 1.

Download Naka et al. supplementary movie(Video)
Video 9 MB

Naka et al. supplementary movie

3D view of field pressure--spanwise velocity correlation Rpw at probe position (b: yp+=48) at Re_ƒÆ=10 000. The correlation is Gaussian filtered with a width of ƒÐ+=18.9. The representation is the same as movie 1.

Download Naka et al. supplementary movie(Video)
Video 4.9 MB

Naka et al. supplementary movie

3D view of field pressure--spanwise velocity correlation Rpw at probe position (b: yp+=48) at Re_ƒÆ=10 000. The correlation is Gaussian filtered with a width of ƒÐ+=18.9. The representation is the same as movie 1.

Download Naka et al. supplementary movie(Video)
Video 11.7 MB

Naka et al. supplementary movie

3D view of field pressure--spanwise velocity correlation Rpw at probe position (h: yp/ƒÂ=0.55) at Re_ƒÆ=10 000. The correlation is Gaussian filtered with a width of ƒÐ+=18.9. The representation is the same as movie 1.

Download Naka et al. supplementary movie(Video)
Video 4.4 MB

Naka et al. supplementary movie

3D view of field pressure--spanwise velocity correlation Rpw at probe position (h: yp/ƒÂ=0.55) at Re_ƒÆ=10 000. The correlation is Gaussian filtered with a width of ƒÐ+=18.9. The representation is the same as movie 1.

Download Naka et al. supplementary movie(Video)
Video 10.3 MB

Naka et al. supplementary movie

Three components of conditional field pressure-velocity correlations at the probe position (c) represented by color (Rpu) and vectors (Rpv and Rpw) for p>0 at Re_ƒÆ=10 000. Distribution in $y-z$ plane is scanned within -2 < ƒ¢tUe/ƒÂ < 9.

Download Naka et al. supplementary movie(Video)
Video 10.5 MB

Naka et al. supplementary movie

Three components of conditional field pressure-velocity correlations at the probe position (c) represented by color (Rpu) and vectors (Rpv and Rpw) for p>0 at Re_ƒÆ=10 000. Distribution in $y-z$ plane is scanned within -2 < ƒ¢tUe/ƒÂ < 9.

Download Naka et al. supplementary movie(Video)
Video 40.7 MB

Naka et al. supplementary movie

Three components of conditional field pressure-velocity correlations at the probe position (c) represented by color (Rpu) and vectors (Rpv and Rpw) for p<0 at Re_ƒÆ=10 000. Distribution in $y-z$ plane is scanned within -0.6 < ƒ¢tUe/ƒÂ < 5.5.

Download Naka et al. supplementary movie(Video)
Video 8.6 MB

Naka et al. supplementary movie

Three components of conditional field pressure-velocity correlations at the probe position (c) represented by color (Rpu) and vectors (Rpv and Rpw) for p<0 at Re_ƒÆ=10 000. Distribution in $y-z$ plane is scanned within -0.6 < ƒ¢tUe/ƒÂ < 5.5.

Download Naka et al. supplementary movie(Video)
Video 32.2 MB