Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-05T09:15:20.908Z Has data issue: false hasContentIssue false
  • English
  • Français

Solute dispersion in bifurcating networks

Published online by Cambridge University Press:  27 August 2020

Robert A. Zimmerman  and
Daniel M. Tartakovsky Open the ORCID record for Daniel M. Tartakovsky [Opens in a new window]
Robert A. Zimmerman
Affiliation:
Los Alamos National Laboratory, Los Alamos, NM87545, USA
Daniel M. Tartakovsky*
Affiliation:
Department of Energy Resources Engineering, Stanford University, 367 Panama Street, Stanford, CA94305, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

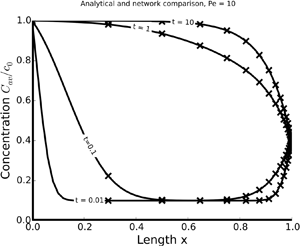
Advective–diffusive transport of passive scalars in confined environments (e.g. vessels and channels) within a network is of fundamental importance in a plethora of biological and geophysical phenomena. We conduct a leading-order analysis, consistent with the theory of hydrodynamic dispersion, which averages out the radial variability within a vessel. One-dimensional solutions for individual vessels (edges of a network), obtained for arbitrary (undefined) transient Dirichlet boundary conditions, serve as a building block for a network model. A network transport solution is developed by iteratively linking single-vessel solutions to each other in a bifurcating fractal tree model, i.e. at nodes of the network. We find transport behaviour to be strongly affected by the network geometry and daughter vessels to significantly impact the rate of transport in the upstream parent vessels.

JFM classification

Biological Fluid Dynamics: Biomedical flows Low-Reynolds-number flows: Porous media
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 901 , 25 October 2020 , A24
Check for updates
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Adam, J. A. 2011 Blood vessel branching: beyond the standard calculus problem. Math. Mag. 84 (3), 196–207.CrossRefGoogle Scholar
Aris, R. 1956 On the dispersion of a solute in a fluid flowing through a tube. Proc. R. Soc. Lond. A 235 (1200), 67–77.Google Scholar
Beard, D. A. & Bassingthwaighte, J. B. 2000 Advection and diffusion of substances in biological tissues with complex vascular networks. Ann. Biomed. Engng 28 (3), 253–268.CrossRefGoogle ScholarPubMed
Beard, D. A. & Bassingthwaighte, J. B. 2001 Modeling advection and diffusion of oxygen in complex vascular networks. Ann. Biomed. Engng 29 (4), 298–310.CrossRefGoogle ScholarPubMed
Berg, M., Davit, Y., Quintard, M. & Lorthois, S. 2020 Modelling solute transport in the brain microcirculation: is it really well mixed inside the blood vessels? J. Fluid Mech. 884, A39.CrossRefGoogle Scholar
Bruderer, C. & Bernabé, Y. 2001 Network modeling of dispersion: transition from Taylor dispersion in homogeneous networks to mechanical dispersion in very heterogeneous ones. Water Resour. Res. 37 (4), 897–908.CrossRefGoogle Scholar
Cabrales, P., Tsai, A. G., Winslow, R. M. & Intaglietta, M. 2005 Extreme hemodilution with PEG-hemoglobin vs. PEG-albumin. Am. J. Physiol. Heart. Circ. Physiol. 289, H2392–H2400.CrossRefGoogle ScholarPubMed
Cairney, J. W. G. 1992 Translocation of solutes in ectomycorrhizal and saprotrophic rhizomorphs. Mycological Res. 96 (2), 135–141.CrossRefGoogle Scholar
Cousins, W. & Gremaud, P. A. 2012 Boundary conditions for hemodynamics: the structured tree revisited. J. Comput. Phys. 231 (18), 6086–6096.CrossRefGoogle Scholar
Cousins, W., Gremaud, P. A. & Tartakovsky, D. M. 2013 A new physiological boundary condition for hemodynamics. SIAM J. Appl. Maths 73 (3), 1203–1223.CrossRefGoogle Scholar
Dailey, S. E., Dysart, C. B., Langan, D. R., Slye, M. J., Nuttal, G. A., Schrader, L. M., Williams, B. A. & Oliver, W. C. 2005 An in vitro study comparing the effects of Hextend, Hespan, normal saline, and lactated Ringer's solution on thrombelastography and the activated partial thromboplastin time. Cardiothorac. Vasc. Anesth. 19 (3), 358–361.CrossRefGoogle Scholar
Datta, B. N. 2010 Numerical Linear Algebra and Applications, vol. 116. SIAM.CrossRefGoogle Scholar
Fung, Y. C. & Tang, H. T. 1975 Longitudinal dispersion of tracer particles in the blood flowing in a pulmonary alveolar sheet. J. Appl. Mech. 42 (3), 536–540.CrossRefGoogle Scholar
Gentile, F., Ferrari, M. & Decuzzi, P. 2008 The transport of nanoparticles in blood vessels: the effect of vessel permeability and blood rheology. Ann. Biomed. Engng 36 (2), 254–261.CrossRefGoogle ScholarPubMed
Gisladottir, V. R., Roubinet, D. & Tartakovsky, D. M. 2016 Particle methods for heat transfer in fractured media. Transp. Porous Med. 115 (2), 311–326.CrossRefGoogle Scholar
Goldman, D. 2008 Theoretical models of microvascular oxygen transport to tissue. Microcirculation 15 (8), 795–811.CrossRefGoogle ScholarPubMed
Goldman, D. & Popel, A. S. 2000 A computational study of the effect of capillary network anastomoses and tortuosity on oxygen transport. J. Theor. Biol. 206 (2), 181–194.CrossRefGoogle ScholarPubMed
Green, H. D. 1944 Circulation: physical principles. In Medical Physics (ed. Glasser, O.). The Year Book Publishers, Inc.Google Scholar
Hansen, E. R. 1975 A Table of Series and Products. Prentice-Hall.Google Scholar
Heaton, L. L. M., López, E, Maini, P. K., Fricker, M. D. & Jones, N. S. 2012 a Advection, diffusion, and delivery over a network. Phys. Rev. E 86, 021905.CrossRefGoogle ScholarPubMed
Heaton, L., Obara, B., Grau, V., Jones, N. S., Nakagaki, T., Boddy, L. & Fricker, M. D. 2012 b Analysis of fungal networks. Fungal Biol. Rev. 26 (1), 12–29.CrossRefGoogle Scholar
Hellums, J. D., Nair, P. K., Huang, N. S. & Ohshima, N. 1995 Simulation of intraluminal gas transport processes in the microcirculation. Ann. Biomed. Engng 24 (1), 1–24.CrossRefGoogle Scholar
Hollenbeck, K. J. 1998 INVLAP.M: a Matlab function for numerical inversion of Laplace transforms by the de Hoog algorithm. http://www.isva.dtu.dk/staff/karl/invlap.htm.Google Scholar
Jennings, D. H. 1987 Translocation of solutes in fungi. Biol. Rev. 62 (3), 215–243.CrossRefGoogle Scholar
Koffie, R. M., Farrar, C. T., Saidi, L.-J., William, C. M., Hyman, B. T. & Spires-Jones, T. L. 2011 Nanoparticles enhance brain delivery of blood–brain barrier-impermeable probes for in vivo optical and magnetic resonance imaging. Proc. Natl Acad. Sci. USA 108 (46), 18837–18842.CrossRefGoogle ScholarPubMed
Lee, J.-S. & Fung, Y.-C. 1971 Flow in nonuniform small blood vessels. Microvasc. Res. 3 (3), 272–287.CrossRefGoogle ScholarPubMed
Mäkelä, A. 2002 Derivation of stem taper from the pipe theory in a carbon balance framework. Tree Physiol. 22 (13), 891–905.CrossRefGoogle Scholar
McCulloh, K. A., Sperry, J. S. & Adler, F. R. 2003 Water transport in plants obeys Murray's law. Nature 421 (6926), 939–942.CrossRefGoogle ScholarPubMed
Minamino, R. & Tateno, M. 2014 Tree branching: Leonardo da Vinci's rule versus biomechanical models. PloS One 9 (4), e93535.CrossRefGoogle Scholar
Olufsen, M. S. 1999 Structured tree outflow condition for blood flow in larger systemic arteries. Am. J. Physiol. Heart Circ. Physiol. 276 (1), H257–H268.CrossRefGoogle ScholarPubMed
Olufsen, M. S., Peskin, C. S., Kim, W. Y., Pedersen, E. M., Nadim, A. & Larsen, J. 2000 Numerical simulation and experimental validation of blood flow in arteries with structured-tree outflow conditions. Ann. Biomed. Engng 28 (11), 1281–1299.CrossRefGoogle ScholarPubMed
Popel, A. S. & Gross, J. F. 1979 Analysis of oxygen diffusion from arteriolar networks. Am. J. Physiol. Heart Circ. Physiol. 237 (6), H681–H689.CrossRefGoogle ScholarPubMed
Pries, A. R., Secomb, T. W., Gaehtgens, P. & Gross, J. F. 1990 Blood flow in microvascular networks. Experiments and simulation. Circ. Res. 67 (4), 826–834.CrossRefGoogle ScholarPubMed
Roubinet, D., de Dreuzy, J.-R. & Tartakovsky, D. M. 2013 Particle-tracking simulations of anomalous transport in hierarchically fractured rocks. Comput. Geosci. 50, 52–58.CrossRefGoogle Scholar
Sack, L. & Holbrook, N. M. 2006 Leaf hydraulics. Annu. Rev. Plant Biol. 57, 361–381.CrossRefGoogle ScholarPubMed
Sarpkaya, T. 1966 Experimental determination of the critical Reynolds number for pulsating Poiseuille flow. J. Basic Engng 88 (3), 589–598.CrossRefGoogle Scholar
Shaw, S. & Murthy, P. V. S. N. 2010 Magnetic targeting in the impermeable microvessel with two-phase fluid model–Non-Newtonian characteristics of blood. Microvasc. Res. 80, 209–220.CrossRefGoogle ScholarPubMed
Shipley, R. J. & Chapman, S. J. 2010 Multiscale modelling of fluid and drug transport in vascular tumours. Bull. Math. Biol. 72 (6), 1464–1491.CrossRefGoogle ScholarPubMed
Sriram, K., Intaglietta, M. & Tartakovsky, D. M. 2014 a Hematocrit dispersion in asymmetrically bifurcating vascular networks. Am. J. Physiol. Heart Circ. Physiol. 307 (11), H1576–H1586.CrossRefGoogle ScholarPubMed
Sriram, K., Intaglietta, M. & Tartakovsky, D. M. 2014 b Non-Newtonian flow of blood in arterioles: consequences for wall shear stress measurements. Microcirculation 21 (7), 628–639.CrossRefGoogle ScholarPubMed
Sriram, K., Vazquez, B. Y. S., Tsai, A. G., Cabrales, P., Intaglietta, M. & Tartakovsky, D. M. 2012 Autoregulation and mechanotransduction control the arteriolar response to small changes in hematocrit. Am. J. Physiol. Heart Circ. Physiol. 303 (9), H1096–H1106.CrossRefGoogle ScholarPubMed
Uylings, H. B. M. 1977 Optimization of diameters and bifurcation angles in lung and vascular tree structures. Bull. Math. Biol. 39 (5), 509–520.CrossRefGoogle ScholarPubMed
Womersley, J. R. 1955 Method for the calculation of velocity, rate of flow and viscous drag in arteries when the pressure gradient is known. J. Physiol. 127 (3), 553.CrossRefGoogle ScholarPubMed
Young, J. H., Evert, R. F. & Eschrich, W. 1973 On the volume-flow mechanism of phloem transport. Planta 113 (4), 355–366.CrossRefGoogle ScholarPubMed
Zamir, M. 1988 The branching structure of arterial trees. Comments Theor. Biol. 1, 15–37.Google Scholar
Zimmerman, R. A., Jankowski, T. A. & Tartakovsky, D. M. 2016 Analytical models of axisymmetric reaction-diffusion phenomena in composite media. Intl J. Heat Mass Transfer 99, 425–431.CrossRefGoogle Scholar
Zimmerman, R. A., Severino, G. & Tartakovsky, D. M. 2018 Hydrodynamic dispersion in a tube with diffusive losses through its walls. J. Fluid Mech. 837, 546–561.CrossRefGoogle Scholar
Zimmerman, R. A., Tsai, A. G., Intaglietta, M. & Tartakovsky, D. M. 2019 A mechanistic analysis of possible blood transfusion failure to increase circulatory oxygen delivery in anemic patients. Ann. Biomed. Engng 47 (4), 1094–1105.CrossRefGoogle ScholarPubMed