Article contents
Solidification of binary aqueous solutions under periodic cooling. Part 2. Distribution of solid fraction
Published online by Cambridge University Press: 07 May 2019
Abstract
We report an experimental study of the distributions of temperature and solid fraction of growing 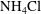 $\text{NH}_{4}\text{Cl}$–
$\text{NH}_{4}\text{Cl}$–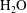 $\text{H}_{2}\text{O}$ mushy layers that are subjected to periodical cooling from below, focusing on late-time dynamics where the mushy layer oscillates about an approximate steady state. Temporal evolution of the local temperature
$\text{H}_{2}\text{O}$ mushy layers that are subjected to periodical cooling from below, focusing on late-time dynamics where the mushy layer oscillates about an approximate steady state. Temporal evolution of the local temperature 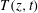 $T(z,t)$ at various heights in the mush demonstrates that the temperature oscillations of the bottom cooling boundary propagate through the mushy layer with phase delays and substantial decay in the amplitude. As the initial concentration
$T(z,t)$ at various heights in the mush demonstrates that the temperature oscillations of the bottom cooling boundary propagate through the mushy layer with phase delays and substantial decay in the amplitude. As the initial concentration 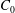 $C_{0}$ increases, we show that the decay rate of the thermal oscillation with height also decreases, and the propagation speed of the oscillation phase increases. We interpret this as a result of the solid fraction increasing with
$C_{0}$ increases, we show that the decay rate of the thermal oscillation with height also decreases, and the propagation speed of the oscillation phase increases. We interpret this as a result of the solid fraction increasing with 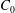 $C_{0}$, which enhances the thermal conductivity but reduces the specific heat of the mushy layer. We present a new methodology to determine the distribution of solid fraction
$C_{0}$, which enhances the thermal conductivity but reduces the specific heat of the mushy layer. We present a new methodology to determine the distribution of solid fraction 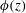 $\unicode[STIX]{x1D719}(z)$ in mushy layers for various
$\unicode[STIX]{x1D719}(z)$ in mushy layers for various 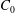 $C_{0}$, using only measurements of the temperature
$C_{0}$, using only measurements of the temperature 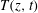 $T(z,t)$. The method is based on the phase behaviour during thermal modulation, and opens up a new approach for inferring mushy-layer properties in geophysical and engineering settings, where direct measurements are challenging. In our experiments, profiles of the solid fraction
$T(z,t)$. The method is based on the phase behaviour during thermal modulation, and opens up a new approach for inferring mushy-layer properties in geophysical and engineering settings, where direct measurements are challenging. In our experiments, profiles of the solid fraction 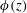 $\unicode[STIX]{x1D719}(z)$ exhibit a cliff–ramp–cliff structure with large vertical gradients of
$\unicode[STIX]{x1D719}(z)$ exhibit a cliff–ramp–cliff structure with large vertical gradients of 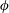 $\unicode[STIX]{x1D719}$ near the mush–liquid interface and also near the bottom boundary, but much more gradual variation in the interior of the mushy layer. Such a profile structure is more pronounced for higher initial concentration
$\unicode[STIX]{x1D719}$ near the mush–liquid interface and also near the bottom boundary, but much more gradual variation in the interior of the mushy layer. Such a profile structure is more pronounced for higher initial concentration 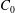 $C_{0}$. For very low concentration, the solid fraction appears to be linearly dependent on the height within the mush. The volume-average of the solid fraction, and the local fluctuations in
$C_{0}$. For very low concentration, the solid fraction appears to be linearly dependent on the height within the mush. The volume-average of the solid fraction, and the local fluctuations in 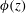 $\unicode[STIX]{x1D719}(z)$ both increase as
$\unicode[STIX]{x1D719}(z)$ both increase as 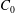 $C_{0}$ increases. We suggest that the fast increase of
$C_{0}$ increases. We suggest that the fast increase of 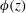 $\unicode[STIX]{x1D719}(z)$ near the bottom boundary is possibly due to diffusive transport of solute away from the bottom boundary and the depletion of solute content near the basal region.
$\unicode[STIX]{x1D719}(z)$ near the bottom boundary is possibly due to diffusive transport of solute away from the bottom boundary and the depletion of solute content near the basal region.
- Type
- JFM Papers
- Information
- Copyright
- © 2019 Cambridge University Press
References
- 3
- Cited by


