Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-23T09:02:43.079Z Has data issue: false hasContentIssue false
  • English
  • Français

Small-scale structure and energy transfer in homogeneous turbulence

Published online by Cambridge University Press:  12 September 2018

Douglas W. Carter Open the ORCID record for Douglas W. Carter [Opens in a new window]  and
Filippo Coletti
Douglas W. Carter
Affiliation:
Department of Aerospace Engineering, University of Minnesota, Minneapolis, MN 55414, USA Saint Anthony Falls Laboratory, Minneapolis, MN 55414, USA
Filippo Coletti*
Affiliation:
Department of Aerospace Engineering, University of Minnesota, Minneapolis, MN 55414, USA Saint Anthony Falls Laboratory, Minneapolis, MN 55414, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We use high-resolution velocity measurements in a jet-stirred zero-mean-flow facility to investigate the topology and energy transfer properties of homogeneous turbulence over the Reynolds number range 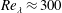$Re_{\unicode[STIX]{x1D706}}\approx 300$–500. The probability distributions of the enstrophy and strain-rate fields show long tails associated with the most intense events, while the weaker events behave as random variables. The high-enstrophy and high-strain structures are shaped as tube-like and sheet-like objects, respectively, the latter often wrapped around the former. Both types of structures have thickness that scales in Kolmogorov units, and display self-similar topology over a wide range of scales. The small-scale turbulence activity is found to be strongly correlated with the large-scale activity, suggesting that the phenomenon of amplitude modulation (previously observed in advection-dominated shear flows) is not limited to specific production mechanisms. Observing the significant variations in spatially averaged enstrophy, we heuristically define hyperactive and sleeping states of the flow: these also correspond to, respectively, high and low levels of large-scale velocity gradients. Moreover, the hyperactive and sleeping states contribute very differently to the inter-scale energy flux, characterized via the nonlinear transfer term in the Kármán–Howarth–Monin equation. While the energy cascades to smaller scales along the jet-axis direction, a weaker but sizable inverse transfer is observed along the transverse direction; a behaviour so far only observed in spatially developing flows. The hyperactive states are characterized by very intense energy transfers, while the sleeping states account for weaker fluxes, largely directed from small to large scales. This implies that the form of energy cascade depends on the presence (or absence) of intense turbulent structures. These results are at odds with the classic concept of the energy cascade between adjacent scales, but are compatible with the view of a cascade in physical space.

JFM classification

Turbulent Flows: Homogeneous turbulence Turbulent Flows: Intermittency Turbulent Flows: Turbulent Flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 854 , 10 November 2018 , pp. 505 - 543
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alexakis, A. 2017 Helically decomposed turbulence. J. Fluid Mech. 812, 752–770.Google Scholar
Alves Portela, F., Papadakis, G. & Vassilicos, J. C. 2017 The turbulence cascade in the near wake of a square prism. J. Fluid Mech. 825, 315–352.Google Scholar
Antonia, R. A., Zhou, T. & Romano, G. P. 2002 Small-scale turbulence characteristics of two-dimensional bluff body wakes. J. Fluid Mech. 459, 67–92.Google Scholar
Aoyama, T., Ishihara, T., Kaneda, Y., Yokokawa, M., Itakura, K. & Uno, A. 2005 Statistics of energy transfer in high-resolution direct numerical simulation of turbulence in a periodic box. J. Phys. Soc. Japan 74 (12), 3202–3212.Google Scholar
Baker, L., Frankel, A., Mani, A. & Coletti, F. 2017 Coherent clusters of inertial particles in homogeneous turbulence. J. Fluid Mech. 833, 364–398.Google Scholar
Bandyopadhyay, P. R. & Hussain, A. K. M. F. 1984 The coupling between scales in shear flows. Phys. Fluids 27 (9), 2221–2228.Google Scholar
Batchelor, G. K. & Stewart, R. W. 1950 Anisotropy of the spectrum of turbulence at small wave-numbers. Q. J. Mech. Appl. Maths 3 (1), 1–8.Google Scholar
Batchelor, G. K. & Townsend, A. A. 1949 The nature of turbulent motion at large wave-numbers. Proc. R. Soc. Lond. A 199 (1057), 238–255.Google Scholar
Bellani, G. & Variano, E. A. 2014 Homogeneity and isotropy in a laboratory turbulent flow. Exp. Fluids 55 (1), 1646.Google Scholar
Benedict, L. H. & Gould, R. D. 1996 Towards better uncertainty estimates for turbulence statistics. Exp. Fluids 22 (2), 129–136.Google Scholar
Bermejo-Moreno, I., Pullin, D. I. & Horiuti, K. 2009 Geometry of enstrophy and dissipation, grid resolution effects and proximity issues in turbulence. J. Fluid Mech. 620, 121–166.Google Scholar
Bewley, G. P., Chang, K., Bodenschatz, E.& International Collaboration for Turbulence Research 2012 On integral length scales in anisotropic turbulence. Phys. Fluids 24 (6), 061702.Google Scholar
Biferale, L. 2003 Shell models of energy cascade in turbulence. Annu. Rev. Fluid Mech. 35 (1), 441–468.Google Scholar
Biferale, L., Musacchio, S. & Toschi, F. 2012 Inverse energy cascade in three-dimensional isotropic turbulence. Phys. Rev. Lett. 108 (16), 164501.Google Scholar
Biferale, L. & Toschi, F. 2001 Anisotropic homogeneous turbulence: hierarchy and intermittency of scaling exponents in the anisotropic sectors. Phys. Rev. Lett. 86 (21), 4831.Google Scholar
Blum, D. B., Bewley, G. P., Bodenschatz, E., Gibert, M., Gylfason, A., Mydlarski, L., Voth, G. A., Xu, H. & Yeung, P. K. 2011 Signatures of non-universal large scales in conditional structure functions from various turbulent flows. New J. Phys. 13 (11), 113020.Google Scholar
Buxton, O. R. H. & Ganapathisubramani, B. 2010 Amplification of enstrophy in the far field of an axisymmetric turbulent jet. J. Fluid Mech. 651, 483–502.Google Scholar
Buxton, O. R. H. & Ganapathisubramani, B. 2014 Concurrent scale interactions in the far-field of a turbulent mixing layer. Phys. Fluids 26 (12), 125106.Google Scholar
Buxton, O. R. H., Breda, M. & Chen, X. 2017 Invariants of the velocity-gradient tensor in a spatially developing inhomogeneous turbulent flow. J. Fluid Mech. 817, 1–20.Google Scholar
Buzzicotti, M., Bhatnagar, A., Biferale, L., Lanotte, A. S. & Ray, S. S. 2016 Lagrangian statistics for Navier–Stokes turbulence under Fourier-mode reduction: fractal and homogeneous decimations. New J. Phys. 18 (11), 113047.Google Scholar
Cadot, O., Douady, S. & Couder, Y. 1995 Characterization of the low-pressure filaments in a three-dimensional turbulent shear flow. Phys. Fluids 7 (3), 630–646.Google Scholar
Cardesa, J. I., Mistry, D., Gan, L. & Dawson, J. R. 2013 Invariants of the reduced velocity gradient tensor in turbulent flows. J. Fluid Mech. 716, 597–615.Google Scholar
Cardesa, J., Vela-Martín, A., Dong, S. & Jiménez, J. 2015 The temporal evolution of the energy flux across scales in homogeneous turbulence. Phys. Fluids 27 (11), 111702.Google Scholar
Cardesa, J. I., Vela-Martín, A. & Jiménez, J. 2017 The turbulent cascade in five dimensions. Science 357 (6353), 782–784.Google Scholar
Carter, D., Petersen, A., Amili, O. & Coletti, F. 2016 Generating and controlling homogeneous air turbulence using random jet arrays. Exp. Fluids 57 (12), 189.Google Scholar
Carter, D. W. & Coletti, F. 2017 Scale-to-scale anisotropy in homogeneous turbulence. J. Fluid Mech. 827, 250–284.Google Scholar
Catrakis, H. J. & Dimotakis, P. E. 1996 Scale distributions and fractal dimensions in turbulence. Phys. Rev. Lett. 77 (18), 3795.Google Scholar
Chen, S., Sreenivasan, K. R. & Nelkin, M. 1997 Inertial range scalings of dissipation and enstrophy in isotropic turbulence. Phys. Rev. Lett. 79 (7), 1253.Google Scholar
Chevillard, L. & Meneveau, C. 2007 Intermittency and universality in a Lagrangian model of velocity gradients in three-dimensional turbulence. C. R. Méc 335 (4), 187–193.Google Scholar
Chien, C.-C., Blum, D. B. & Voth, G. A. 2013 Effects of fluctuating energy input on the small scales in turbulence. J. Fluid Mech. 737, 527–551.Google Scholar
Chung, D. & McKeon, B. J. 2010 Large-eddy simulation of large-scale structures in long channel flow. J. Fluid Mech. 661, 341–364.Google Scholar
Danaila, L., Antonia, R. A. & Burattini, P. 2012 Comparison between kinetic energy and passive scalar energy transfer in locally homogeneous isotropic turbulence. Physica D 241 (3), 224–231.Google Scholar
Davidson, P. A. 2004 Turbulence. An Introduction for Scientists and Engineers. Oxford University Press.Google Scholar
De Silva, C. M., Gnanamanickam, E. P., Atkinson, C., Buchmann, N. A., Hutchins, N., Soria, J. & Marusic, I. 2014 High spatial range velocity measurements in a high Reynolds number turbulent boundary layer. Phys. Fluids 26 (2), 025117.Google Scholar
Del Álamo, J. C. & Jiménez, J. 2009 Estimation of turbulent convection velocities and corrections to Taylor’s approximation. J. Fluid Mech. 640, 5–26.Google Scholar
Discetti, S. & Coletti, F. 2018 Volumetric velocimetry for fluid flows. Meas. Sci. Technol. 29 (4), 042001.Google Scholar
Domaradzki, J. A. & Carati, D. 2007 An analysis of the energy transfer and the locality of nonlinear interactions in turbulence. Phys. Fluids 19 (8), 085112.Google Scholar
Dong, S., Lozano-Durán, A., Sekimoto, A. & Jiménez, J. 2017 Coherent structures in statistically stationary homogeneous shear turbulence. J. Fluid Mech. 816, 167–208.Google Scholar
Douady, S., Couder, Y. & Brachet, M. E. 1991 Direct observation of the intermittency of intense vorticity filaments in turbulence. Phys. Rev. Lett. 67 (8), 983.Google Scholar
Elsinga, G. E., Ishihara, T., Goudar, M. V., da Silva, C. B. & Hunt, J. C. R. 2017 The scaling of straining motions in homogeneous isotropic turbulence. J. Fluid Mech. 829, 31–64.Google Scholar
Elsinga, G. E. & Marusic, I. 2010 Universal aspects of small-scale motions in turbulence. J. Fluid Mech. 662, 514–539.Google Scholar
Fiscaletti, D., Attili, A., Bisetti, F. & Elsinga, G. E. 2016 Scale interactions in a mixing layer: the role of the large-scale gradients. J. Fluid Mech. 791, 154–173.Google Scholar
Fiscaletti, D., Ganapathisubramani, B. & Elsinga, G. E. 2015 Amplitude and frequency modulation of the small scales in a jet. J. Fluid Mech. 772, 756–783.Google Scholar
Fiscaletti, D., Westerweel, J. & Elsinga, G. E. 2014 Long-range μPIV to resolve the small scales in a jet at high Reynolds number. Exp. Fluids 55 (9), 1812.Google Scholar
Frisch, U. 1995 Turbulence: The Legacy of AN Kolmogorov. Cambridge University Press.Google Scholar
Frisch, U., Pomyalov, A., Procaccia, I. & Ray, S. S. 2012 Turbulence in noninteger dimensions by fractal Fourier decimation. Phys. Rev. Lett. 108 (7), 074501.Google Scholar
Ganapathisubramani, B., Hutchins, N., Monty, J. P., Chung, D. & Marusic, I. 2012 Amplitude and frequency modulation in wall turbulence. J. Fluid Mech. 712, 61–91.Google Scholar
Ganapathisubramani, B., Lakshminarasimhan, K. & Clemens, N. T. 2008 Investigation of three-dimensional structure of fine scales in a turbulent jet by using cinematographic stereoscopic particle image velocimetry. J. Fluid Mech. 598, 141–175.Google Scholar
George, W. K. 1992 The decay of homogeneous isotropic turbulence. Phys. Fluids A 4 (7), 1492–1509.Google Scholar
George, W. K. & Hussein, H. J. 1991 Locally axisymmetric turbulence. J. Fluid Mech. 233, 1–23.Google Scholar
Gomes-Fernandes, R., Ganapathisubramani, B. & Vassilicos, J. C. 2015 The energy cascade in near-field non-homogeneous non-isotropic turbulence. J. Fluid Mech. 771, 676–705.Google Scholar
Goto, S. 2008 A physical mechanism of the energy cascade in homogeneous isotropic turbulence. J. Fluid Mech. 605, 355–366.Google Scholar
Graham, M. D. 2014 Drag reduction and the dynamics of turbulence in simple and complex fluids. Phys. Fluids 26 (10), 625–656.Google Scholar
Guala, M., Metzger, M. & McKeon, B. J. 2010 Intermittency in the atmospheric surface layer: Unresolved or slowly varying? Physica D 239 (14), 1251–1257.Google Scholar
Hearst, R. J., Buxton, O. R. H., Ganapathisubramani, B. & Lavoie, P. 2012 Experimental estimation of fluctuating velocity and scalar gradients in turbulence. Exp. Fluids 53 (4), 925–942.Google Scholar
Herbert, E., Daviaud, F., Dubrulle, B., Nazarenko, S. & Naso, A. 2012 Dual non-Kolmogorov cascades in a von Kármán flow. Europhys. Lett. 100 (4), 44003.Google Scholar
Herpin, S., Stanislas, M., Foucaut, J. M. & Coudert, S. 2013 Influence of the Reynolds number on the vortical structures in the logarithmic region of turbulent boundary layers. J. Fluid Mech. 716, 5–50.Google Scholar
Hill, R. J. 1997 Applicability of Kolmogorov’s and Monin’s equations of turbulence. J. Fluid Mech. 353, 67–81.Google Scholar
Hill, R. J. 2002 Exact second-order structure-function relationships. J. Fluid Mech. 468, 317–326.Google Scholar
Hunt, J. C. R., Ishihara, T., Worth, N. A. & Kaneda, Y. 2014 Thin shear layer structures in high Reynolds number turbulence. Flow Turbul. Combust. 92 (3), 607–649.Google Scholar
Hutchins, N. & Marusic, I. 2007 Large-scale influences in near-wall turbulence. Phil. Trans. R. Soc. Lond. A 365 (1852), 647–664.Google Scholar
Iqbal, M. O. & Thomas, F. O. 2007 Coherent structure in a turbulent jet via a vector implementation of the proper orthogonal decomposition. J. Fluid Mech. 571, 281–326.Google Scholar
Ishihara, T., Gotoh, T. & Kaneda, Y. 2009 Study of high-Reynolds number isotropic turbulence by direct numerical simulation. Annu. Rev. Fluid Mech. 41, 165–180.Google Scholar
Ishihara, T., Kaneda, Y. & Hunt, J. C. 2013 Thin shear layers in high Reynolds number turbulence DNS results. Flow Turbul. Combust. 91 (4), 895–929.Google Scholar
Jiménez, J. 2012 Cascades in wall-bounded turbulence. Annu. Rev. Fluid Mech. 44, 27–45.Google Scholar
Jiménez, J. & Moin, P. 1991 The minimal flow unit in near-wall turbulence. J. Fluid Mech. 225, 213–240.Google Scholar
Jiménez, J. & Wray, A. A. 1998 On the characteristics of vortex filaments in isotropic turbulence. J. Fluid Mech. 373, 255–285.Google Scholar
Jiménez, J., Wray, A. A., Saffman, P. G. & Rogallo, R. S. 1993 The structure of intense vorticity in isotropic turbulence. J. Fluid Mech. 255, 65–90.Google Scholar
Kerr, R. M. 1985 Higher-order derivative correlations and the alignment of small-scale structures in isotropic numerical turbulence. J. Fluid Mech. 153, 31–58.Google Scholar
Kolmogorov, A. N. 1941 The local structure of turbulence in incompressible viscous fluid for very large Reynolds numbers. Dokl. Akad. Nauk SSSR 30, 299–303.Google Scholar
Kolmogorov, A. N. 1962 A refinement of previous hypotheses concerning the local structure of turbulence in a viscous incompressible fluid at high Reynolds number. J. Fluid Mech. 13 (1), 82–85.Google Scholar
Kuo, A. Y.-S. & Corrsin, S. 1971 Experiments on internal intermittency and fine-structure distribution functions in fully turbulent fluid. J. Fluid Mech. 50 (2), 285–319.Google Scholar
Lamriben, C., Cortet, P.-P. & Moisy, F. 2011 Direct measurements of anisotropic energy transfers in a rotating turbulence experiment. Phys. Rev. Lett. 107 (2), 024503.Google Scholar
Landau, L. D. & Lifshitz, E. M. 1959 Course of Theoretical Physics, vol. 6: Fluid Mechanics, Pergamon Press.Google Scholar
Lanotte, A. S., Benzi, R., Malapaka, S. K., Toschi, F. & Biferale, L. 2015 Turbulence on a fractal Fourier set. Phys. Rev. Lett. 115 (26), 264502.Google Scholar
Lawson, J. M. & Dawson, J. R. 2015 On velocity gradient dynamics and turbulent structure. J. Fluid Mech. 780, 60–98.Google Scholar
Leung, T., Swaminathan, N. & Davidson, P. A. 2012 Geometry and interaction of structures in homogeneous isotropic turbulence. J. Fluid Mech. 710, 453–481.Google Scholar
Lozano-Durán, A., Flores, O. & Jiménez, J. 2012 The three-dimensional structure of momentum transfer in turbulent channels. J. Fluid Mech. 694, 100–130.Google Scholar
Lozano-Durán, A. & Jiménez, J. 2014 Time-resolved evolution of coherent structures in turbulent channels: characterization of eddies and cascades. J. Fluid Mech. 759, 432–471.Google Scholar
Lüthi, B., Tsinober, A. & Kinzelbach, W. 2005 Lagrangian measurement of vorticity dynamics in turbulent flow. J. Fluid Mech. 528, 87–118.Google Scholar
Mandelbrot, B. B. 1974 Intermittent turbulence in self-similar cascades: divergence of high moments and dimension of the carrier. J. Fluid Mech. 62 (2), 331–358.Google Scholar
Mandelbrot, B. B. 1982 The Fractal Geometry of Nature. Freeman.Google Scholar
Meneveau, C. & Sreenivasan, K. R. 1991 The multifractal nature of turbulent energy dissipation. J. Fluid Mech. 224, 429–484.Google Scholar
Meneveau, C. & Katz, J. 2000 Scale-invariance and turbulence models for large-eddy simulation. Annu. Rev. Fluid Mech. 32 (1), 1–32.Google Scholar
Meneveau, C. & Lund, T. S. 1994 On the Lagrangian nature of the turbulence energy cascade. Phys. Fluids 6 (8), 2820–2825.Google Scholar
Meneveau, C. & Sreenivasan, K. R. 1991 The multifractal nature of turbulent energy dissipation. J. Fluid Mech. 224, 429–484.Google Scholar
Mi, J. & Antonia, R. A. 2010 Approach to local axisymmetry in a turbulent cylinder wake. Exp. Fluids 48 (6), 933–947.Google Scholar
Moisy, F. & Jiménez, J. 2004 Geometry and clustering of intense structures in isotropic turbulence. J. Fluid Mech. 513, 111–133.Google Scholar
Monin, A. S. & Yaglom, A. M. 1975 Statistical Fluid Mechanics (ed. Lumley, J.). MIT Press.Google Scholar
Mouri, H., Takaoka, M., Hori, A. & Kawashima, Y. 2006 On Landau’s prediction for large-scale fluctuation of turbulence energy dissipation. Phys. Fluids 18 (1), 015103.Google Scholar
Mydlarski, L. & Warhaft, Z. 1996 On the onset of high-Reynolds-number grid-generated wind tunnel turbulence. J. Fluid Mech. 320, 331–368.Google Scholar
Nelkin, M. 1999 Enstrophy and dissipation must have the same scaling exponent in the high Reynolds number limit of fluid turbulence. Phys. Fluids 11 (8), 2202–2204.Google Scholar
Obukhov, A. M. 1941 On the distribution of energy in the spectrum of turbulent flow. Bull. Acad. Sci. USSR Ser. Geophys. 5, 453–466.Google Scholar
Ouellette, N. T., Xu, H., Bourgoin, M. & Bodenschatz, E. 2006 Small-scale anisotropy in Lagrangian turbulence. New J. Phys. 8 (6), 102.Google Scholar
Paris, G. & Frisch, U.1985 In Turbulence and Predictability in Geophysical Fluid Dynamics and Climate Dynamics (ed. M. Ghil, R. Benzi & G. Parisi). Elsevier Science.Google Scholar
Perry, A. E. & Chong, M. S. 1994 Topology of flow patterns in vortex motions and turbulence. Appl. Sci. Res. 53 (3–4), 357–374.Google Scholar
Piomelli, U., Cabot, W. H., Moin, P. & Sangsan, L. 1991 Subgrid-scale backscatter in turbulent and transitional flows. Phys. Fluids A 3 (7), 1766–1771.Google Scholar
Qian, J. 1997 Inertial range and the finite Reynolds number effect of turbulence. Phys. Rev. E 55 (1), 337.Google Scholar
Rabey, P. K., Wynn, A. & Buxton, O. R. H. 2015 The kinematics of the reduced velocity gradient tensor in a fully developed turbulent free shear flow. J. Fluid Mech. 767, 627–658.Google Scholar
Ray, S. S. 2015 Thermalized solutions, statistical mechanics and turbulence: an overview of some recent results. Pramana 84 (3), 395–407.Google Scholar
Richardson, L. F. 1920 The supply of energy from and to atmospheric eddies. Proc. R. Soc. Lond. A 97 (686), 354–373.Google Scholar
Rogers, M. M. & Moin, P. 1987 The structure of the vorticity field in homogeneous turbulent flows. J. Fluid Mech. 176, 33–66.Google Scholar
Saddoughi, S. G. & Veeravalli, S. V. 1994 Local isotropy in turbulent boundary layers at high Reynolds number. J. Fluid Mech. 268, 333–372.Google Scholar
Saw, E.-W., Debue, P., Kuzzay, D., Daviaud, F. & Dubrulle, B. 2018 On the universality of anomalous scaling exponents of structure functions in turbulent flows. J. Fluid Mech. 837, 657–669.Google Scholar
Saw, E.-W., Kuzzay, D., Faranda, D., Guittonneau, A., Daviaud, F., Wiertel-Gasquet, C., Padilla, V. & Dubrulle, B. 2016 Experimental characterization of extreme events of inertial dissipation in a turbulent swirling flow. Nat. Commun. 7, 12466.Google Scholar
Schanz, D., Gesemann, S. & Schröder, A. 2016 Shake-the-box: Lagrangian particle tracking at high particle image densities. Exp. Fluids 57 (5), 70.Google Scholar
Schmitt, C. G. & Heymsfield, A. J. 2010 The dimensional characteristics of ice crystal aggregates from fractal geometry. J. Atmos. Sci. 67 (5), 1605–1616.Google Scholar
Schumacher, J., Scheel, J. D., Krasnov, D., Donzis, D. A., Yakhot, V. & Sreenivasan, K. R. 2014 Small-scale universality in fluid turbulence. Proc. Natl Acad. Sci. 111 (30), 10961–10965.Google Scholar
She, Z.-S., Jackson, E. & Orszag, S. A. 1990 Intermittent vortex structures in homogeneous isotropic turbulence. Nature 344 (6263), 226.Google Scholar
She, Z.-S., Jackson, E. & Orszag, S. A. 1991 Structure and dynamics of homogeneous turbulence: models and simulations. Proc. R. Soc. Lond. A 434 (1890), 101–124.Google Scholar
She, Z.-S. & Leveque, E. 1994 Universal scaling laws in fully developed turbulence. Phys. Rev. Lett. 72 (3), 336.Google Scholar
Shen, X. & Warhaft, Z. 2000 The anisotropy of the small scale structure in high Reynolds number (r𝜆1000) turbulent shear flow. Phys. Fluids 12 (11), 2976–2989.Google Scholar
Siggia, E. D. 1981 Numerical study of small-scale intermittency in three-dimensional turbulence. J. Fluid Mech. 107, 375–406.Google Scholar
de Silva, C. M., Philip, J., Chauhan, K., Meneveau, C. & Marusic, I. 2013 Multiscale geometry and scaling of the turbulent–nonturbulent interface in high Reynolds number boundary layers. Phys. Rev. Lett. 111 (4), 044501.Google Scholar
Soria, J., Sondergaard, R., Cantwell, B. J., Chong, M. S. & Perry, A. E. 1994 A study of the fine-scale motions of incompressible time-developing mixing layers. Phys. Fluids 6 (2), 871–884.Google Scholar
Sreenivasan, K. R. 1991 Fractals and multifractals in fluid turbulence. Annu. Rev. Fluid Mech. 23 (1), 539–604.Google Scholar
Sreenivasan, K. R. & Meneveau, C. 1986 The fractal facets of turbulence. J. Fluid Mech. 173, 357–386.Google Scholar
Sreenivasan, K. R. & Antonia, R. A. 1997 The phenomenology of small-scale turbulence. Annu. Rev. Fluid Mech. 29 (1), 435–472.Google Scholar
Tang, D. & Marangoni, A. G. 2006 Microstructure and fractal analysis of fat crystal networks. J. Am. Oil Chem. Soc. 83 (5), 377–388.Google Scholar
Tsinober, A. 2001 An Informal Introduction to Turbulence. Springer.Google Scholar
Tsinober, A., Ortenberg, M. & Shtilman, L. 1999 On depression of nonlinearity in turbulence. Phys. Fluids 11 (8), 2291–2297.Google Scholar
Valente, P. C. & Vassilicos, J. C. 2015 The energy cascade in grid-generated non-equilibrium decaying turbulence. Phys. Fluids 27 (4), 045103.Google Scholar
Variano, E. A. & Cowen, E. A. 2008 A random-jet-stirred turbulence tank. J. Fluid Mech. 604, 1–32.Google Scholar
Vassilicos, J. C. 2015 Dissipation in turbulent flows. Annu. Rev. Fluid Mech. 47, 95–114.Google Scholar
Vincent, A. & Meneguzzi, M. 1994 The dynamics of vorticity tubes in homogeneous turbulence. J. Fluid Mech. 258, 245–254.Google Scholar
von Kármán, T. & Howarth, L. 1938 On the statistical theory of isotropic turbulence. Proc. R. Soc. Lond. A 164 (917), 192–215.Google Scholar
Voth, G. A., la Porta, A., Crawford, A. M., Alexander, J. & Bodenschatz, E. 2002 Measurement of particle accelerations in fully developed turbulence. J. Fluid Mech. 469, 121–160.Google Scholar
Waleffe, F. 1992 The nature of triad interactions in homogeneous turbulence. Phys. Fluids A 4 (2), 350–363.Google Scholar
Westerweel, J., Elsinga, G. E. & Adrian, R. J. 2013 Particle image velocimetry for complex and turbulent flows. Annu. Rev. Fluid Mech. 45, 409–436.Google Scholar
Worth, N. A. & Nickels, T. B. 2011 Time-resolved volumetric measurement of fine-scale coherent structures in turbulence. Phys. Rev. E 84 (2), 025301.Google Scholar
Xu, H., Pumir, A., Falkovich, G., Bodenschatz, E., Shats, M., Xia, H., Francois, N. & Boffetta, G. 2014 Flight-crash events in turbulence. Proc. Natl Acad. Sci. USA 111 (21), 7558–7563.Google Scholar
Yang, Y., Pullin, D. I. & Bermejo-Moreno, I. 2010 Multi-scale geometric analysis of Lagrangian structures in isotropic turbulence. J. Fluid Mech. 654, 233–270.Google Scholar
Yeung, P. K. & Brasseur, J. G. 1991 The response of isotropic turbulence to isotropic and anisotropic forcing at the large scales. Phy. Fluids A 3 (5), 884–897.Google Scholar
Yeung, P. K., Donzis, D. A. & Sreenivasan, K. R. 2012 Dissipation, enstrophy and pressure statistics in turbulence simulations at high Reynolds numbers. J. Fluid Mech. 700, 5–15.Google Scholar
Yeung, P. K., Zhai, X. M. & Sreenivasan, K. R. 2015 Extreme events in computational turbulence. Proc. Natl Acad. Sci. 112 (41), 12633–12638.Google Scholar
Zaman, K. B. M. Q. & Hussain, A. K. M. F. 1981 Taylor hypothesis and large-scale coherent structures. J. Fluid Mech. 112, 379–396.Google Scholar
Zhou, J., Adrian, R. J., Balachandar, S. & Kendall, T. M. 1999 Mechanisms for generating coherent packets of hairpin vortices in channel flow. J. Fluid Mech. 387, 353–396.Google Scholar