Hostname: page-component-745bb68f8f-s22k5 Total loading time: 0 Render date: 2025-01-22T13:06:28.982Z Has data issue: false hasContentIssue false
  • English
  • Français

Small-scale interface dynamic modelling based on the geometric method of moments for a two-scale two-phase flow model with a disperse small scale

Published online by Cambridge University Press:  20 January 2025

Arthur Loison Open the ORCID record for Arthur Loison [Opens in a new window] ,
Teddy Pichard Open the ORCID record for Teddy Pichard [Opens in a new window] ,
Samuel Kokh Open the ORCID record for Samuel Kokh [Opens in a new window]  and
Marc Massot Open the ORCID record for Marc Massot [Opens in a new window]
Arthur Loison*
Affiliation:
Institut Polytechnique de Paris, CMAP, CNRS, École polytechnique, Palaiseau 91120, France
Teddy Pichard
Affiliation:
Institut Polytechnique de Paris, CMAP, CNRS, École polytechnique, Palaiseau 91120, France
Samuel Kokh
Affiliation:
Service de Génie Logiciel pour la Simulation, Université Paris-Saclay, CEA, 91191 Gif-sur-Yvette, France
Marc Massot
Affiliation:
Institut Polytechnique de Paris, CMAP, CNRS, École polytechnique, Palaiseau 91120, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

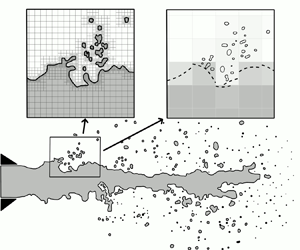
In this contribution, we develop a versatile formalism to derive unified two-phase models describing both the separated and disperse regimes as introduced by Loison et al. (Intl J. Multiphase Flow, vol. 177, 2024, 104857). It relies on the stationary action principle and interface geometric variables. This contribution provides a novel method to derive small-scale models for the dynamics of the interface geometry. They are introduced here on a simplified case where all the scales and phases have the same velocity and that does not take into account large-scale capillary forces. The derivation tools yield a proper mathematical framework through hyperbolicity and signed entropy evolution. The formalism encompasses a hierarchy of small-scale reduced-order models based on a statistical description at a mesoscopic kinetic level and is naturally able to include the description of a disperse phase with polydispersity in size. This hierarchy includes both a cloud of spherical droplets and non-spherical droplets experiencing a dynamical behaviour through incompressible oscillations. The associated small-scale variables are moments of a number density function resulting from the geometric method of moments (GeoMOM). This method selects moments as small-scale geometric variables compatible with the structure and dynamics of the interface; they are defined independently of the flow topology and, therefore, this model allows the coupling of the two-scale flow with an inter-scale transfer. It is shown, in particular, that the resulting dynamics provides partial closures for the interface area density equation obtained from the averaging approach.

JFM classification

Mathematical Foundations: Hamiltonian theory Multiphase and Particle-laden Flows: Gas/liquid flow
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 1003 , 25 January 2025 , A27
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Amsden, A.A., O'Rourke, P.J. & Butler, T.D. 1989 KIVA-II: a computer program for chemically reactive flows with sprays. Tech. Rep. LA-11560-MS, 6228444. Los Alamos National Laboratory.CrossRefGoogle Scholar
Anez, J., Ahmed, A., Hecht, N., Duret, B., Reveillon, J. & Demoulin, F.-X. 2019 Eulerian–Lagrangian spray atomization model coupled with interface capturing method for diesel injectors. Intl J. Multiphase Flow 113, 325–342.CrossRefGoogle Scholar
Baer, M.R. & Nunziato, J.W. 1986 A two-phase mixture theory for the deflagration-to-detonation transition (DDT) in reactive granular materials. Intl J. Multiphase Flow 12 (6), 861–889.CrossRefGoogle Scholar
Bedford, A. 1985 Hamilton's Principle in Continuum Mechanics. Pitman Publishing.Google Scholar
Berdichevsky, V. 2009 Variational Principles of Continuum Mechanics: I. Fundamentals, Interaction of Mechanics and Mathematics, vol. 5. Springer.Google Scholar
Capovilla, R., Guven, J. & Santiago, J.A. 2003 Deformations of the geometry of lipid vesicles. J. Phys. A 36 (23), 6281–6295.CrossRefGoogle Scholar
Caro, F., Coquel, F., Jamet, D. & Kokh, S. 2005 DINMOD: a diffuse interface model for two-phase flows modelling. In IRMA Lectures in Mathematics and Theoretical Physics, pp. 209–237. EMS Press.CrossRefGoogle Scholar
Chanteperdrix, G., Villedieu, P. & Vila, J.-P. 2002 A compressible model for separated two-phase flows computations. In FEDSM2002, vol. 1, pp. 809–816. ASME.CrossRefGoogle Scholar
Cordesse, P. 2020 Contribution to the study of combustion instabilities in cryotechnic rocket engines: coupling diffuse interface models with kinetic-based moment methods for primary atomization simulations. PhD thesis, Université Paris-Saclay.Google Scholar
Cordesse, P., Di Battista, R., Chevalier, Q., Matuszewski, L., Ménard, T., Kokh, S. & Massot, M. 2020 a A diffuse interface approach for disperse two-phase flows involving dual-scale kinematics of droplet deformation based on geometrical variables. ESAIM: Proc. Surv. 69, 24–46.CrossRefGoogle Scholar
Cordesse, P., Remigi, A., Duret, B., Murrone, A., Ménard, T., Demoulin, F.-X. & Massot, M. 2020 b Validation strategy of reduced-order two-fluid flow models based on a hierarchy of direct numerical simulations. Flow Turbul. Combust. 105 (4), 1381–1411.CrossRefGoogle Scholar
Deserno, M. 2015 Fluid lipid membranes: from differential geometry to curvature stresses. Chem. Phys. Lipids 185, 11–45.CrossRefGoogle ScholarPubMed
Devassy, B.M., Habchi, C. & Daniel, E. 2015 Atomization modelling of liquid jets using a two-surface density approach. Atomiz. Sprays 25 (1), 47–80.CrossRefGoogle Scholar
Drew, D.A. 1983 Mathematical modeling of two-phase flow. Annu. Rev. Fluid Mech. 15, 261–291.CrossRefGoogle Scholar
Drew, D.A. 1990 Evolution of geometric statistics. SIAM J. Appl. Math. 50 (3), 649–666.CrossRefGoogle Scholar
Drew, D.A. & Passman, S.L. 1999 Theory of Multicomponent Fluids, Applied Mathematical Sciences, vol. 135. Springer.CrossRefGoogle Scholar
Drui, F., Larat, A., Kokh, S. & Massot, M. 2019 Small-scale kinematics of two-phase flows: identifying relaxation processes in separated- and disperse-phase flow models. J. Fluid Mech. 876, 326–355.CrossRefGoogle Scholar
Dumouchel, C., Blaisot, J.-B., Bouche, E., Ménard, T. & Vu, T.-T. 2015 Multi-scale analysis of atomizing liquid ligaments. Intl J. Multiphase Flow 73, 251–263.CrossRefGoogle Scholar
Essadki, M., de Chaisemartin, S., Laurent, F. & Massot, M. 2018 High order moment model for polydisperse evaporating sprays towards interfacial geometry description. SIAM J. Appl. Maths 78 (4), 2003–2027.CrossRefGoogle Scholar
Essadki, M., de Chaisemartin, S., Massot, M., Laurent, F., Larat, A. & Jay, S. 2016 Adaptive mesh refinement and high order geometrical moment method for the simulation of polydisperse evaporating sprays. Oil Gas Sci. Technol. 71 (5), 01395317.CrossRefGoogle Scholar
Essadki, M., Drui, F., de Chaisemartin, S., Larat, A., Ménard, T. & Massot, M. 2019 Statistical modeling of the gas–liquid interface using geometrical variables: toward a unified description of the disperse and separated phase flows. Intl J. Multiphase Flow 120, 103084.Google Scholar
Estivalezes, J.-L., et al. 2022 A phase inversion benchmark for multiscale multiphase flows. J. Comput. Phys. 450, 110810.CrossRefGoogle Scholar
Fiorina, B., et al. 2016 Modeling challenges in computing aeronautical combustion chambers. Aerosp. Lab J. 5 (11), 1–19.Google Scholar
Fox, R.O. & Marchisio, D.L. (Eds) 2007 Multiphase Reacting Flows: Modelling and Simulation, Courses and Lectures, no. 492. Springer.Google Scholar
Gaillard, P. 2015 Interfaces diffuses et flammes transcritiques LOX/H2. PhD thesis, Universite Pierre et Marie Curie.Google Scholar
Gavrilyuk, S. 2020 ‘Uncertainty’ principle in two fluid-mechanics. ESAIM: Proc. Surv. 69, 47–55.CrossRefGoogle Scholar
Gavrilyuk, S. & Gouin, H. 1999 A new form of governing equations of fluids arising from Hamilton's principle. Intl J. Engng Sci. 37 (12), 1495–1520.CrossRefGoogle Scholar
Gavrilyuk, S., Gouin, H. & Perepechko, Y.V. 1998 Hyperbolic models of homogeneous two-fluid mixtures. Meccanica 33 (2), 161–175.CrossRefGoogle Scholar
Gavrilyuk, S. & Saurel, R. 2002 Mathematical and numerical modeling of two-phase compressible flows with micro-inertia. J. Comput. Phys. 175 (1), 326–360.CrossRefGoogle Scholar
Godlewski, E. & Raviart, P.-A. 1991 Hyperbolic Systems Of Conservation Laws. Springer.Google Scholar
Goldman, R. 2005 Curvature formulas for implicit curves and surfaces. Comput. Aided Geom. Des. 22 (7), 632–658.CrossRefGoogle Scholar
Gouin, H. 2020 Introduction to Mathematical Methods of Analytical Mechanics. ISTE Press/Elsevier.Google Scholar
Gouin, H. & Gavrilyuk, S. 1999 Hamilton's principle and Rankine–Hugoniot conditions for general motions of mixtures. Meccanica 34 (1), 39–47.CrossRefGoogle Scholar
Herivel, J.W. 1955 The derivation of the equations of motion of an ideal fluid by Hamilton's principle. Math. Proc. Camb. Phil. Soc. 51 (2), 344–349.CrossRefGoogle Scholar
Ishii, M. & Hibiki, T. 1975 Thermo-fluid Dynamic Theory of Two-phase Flow. Eyrolles.Google Scholar
Jabin, P.-E. 2002 Various levels of models for aerosols. Math. Models Meth. Appl. Sci. 12 (07), 903–919.CrossRefGoogle Scholar
Jamet, D., Lebaigue, O., Morel, C. & Arcen, B. 2010 Towards a multi-scale approach of two-phase flow modeling in the context of DNB modeling. Nucl. Engng Des. 240 (9), 2131–2138.CrossRefGoogle Scholar
Kah, D., Emre, O., Tran, Q.H., de Chaisemartin, S., Jay, S., Laurent, F. & Massot, M. 2015 High order moment method for polydisperse evaporating sprays with mesh movement: application to internal combustion engines. Intl J. Multiphase Flow 71, 38–65.CrossRefGoogle Scholar
Kreyszig, E. 1991 Differential Geometry. Dover.Google Scholar
Laurent, F. & Massot, M. 2001 Multi-fluid modelling of laminar polydisperse spray flames: origin, assumptions and comparison of sectional and sampling methods. Combust. Theory Model. 5 (4), 537–572.CrossRefGoogle Scholar
Le Touze, C., Dorey, L.-H., Rutard, N. & Murrone, A. 2020 A compressible two-phase flow framework for large eddy simulations of liquid-propellant rocket engines. Appl. Math. Model. 84, 265–286.CrossRefGoogle Scholar
Lebas, R., Menard, T., Beau, P.-A., Berlemont, A. & Demoulin, F.-X. 2009 Numerical simulation of primary break-up and atomization: DNS and modelling study. Intl J. Multiphase Flow 35 (3), 247–260.CrossRefGoogle Scholar
Levermore, C.D. 1996 Moment closure hierarchies for kinetic theories. J. Stat. Phys. 83 (5–6), 1021–1065.CrossRefGoogle Scholar
Lhuillier, D. 2004 Evolution of the volumetric interfacial area in two-phase mixtures. C. R. Méc 332 (2), 103–108.CrossRefGoogle Scholar
Loison, A., Kokh, S., Pichard, T. & Massot, M. 2024 A unified two-scale gas–liquid multi-fluid model with capillarity and interface regularization through a mass transfer between scales. Intl J. Multiphase Flow 177, 104857.CrossRefGoogle Scholar
Marchisio, D.L. & Fox, R.O. 2013 Computational Models for Polydisperse Particulate and Multiphase Systems. Cambridge University Press.CrossRefGoogle Scholar
Massot, M. 2007 Eulerian multi-fluid models for polydisperse evaporating sprays. In Multiphase Reacting Flows: Modelling and Simulation (ed. D.L. Marchisio & R.O. Fox), pp. 79–123. Springer.CrossRefGoogle Scholar
Massot, M., Kumar, M., Gomez, A. & Smooke, M. 1998 Counterflow spray diffusion flames of heptane: computations and experiments. In Proceedings of the 27th Symposium International on Combustion, pp. 1975–1983. The Combustion Institute.CrossRefGoogle Scholar
Mead, L.R. & Papanicolaou, N. 1984 Maximum entropy in the problem of moments. J. Math. Phys. 25 (8), 2404–2417.CrossRefGoogle Scholar
Morel, C. 2015 Mathematical Modeling of Disperse Two-Phase Flows, Fluid Mechanics and its Applications, vol. 114. Springer.CrossRefGoogle Scholar
Ménard, T., Tanguy, S. & Berlemont, A. 2007 Coupling level set/VOF/ghost fluid methods: validation and application to 3D simulation of the primary break-up of a liquid jet. Intl J. Multiphase Flow 33 (5), 510–524.CrossRefGoogle Scholar
O'Rourke, P.J. & Amsden, A.A. 1987 The tab method for numerical calculation of spray droplet breakup. In SAE Tech. Paper 872089.CrossRefGoogle Scholar
Pelanti, M. 2022 Arbitrary-rate relaxation techniques for the numerical modeling of compressible two-phase flows with heat and mass transfer. Intl J. Multiphase Flow 153, 104097.CrossRefGoogle Scholar
Perigaud, G. & Saurel, R. 2005 A compressible flow model with capillary effects. J. Comput. Phys. 209 (1), 139–178.CrossRefGoogle Scholar
Perrier, V. & Gutiérrez, E. 2021 Derivation and closure of Baer and Nunziato type multiphase models by averaging a simple stochastic model. Multiscale Model. Simul. 19 (1), 401–439.CrossRefGoogle Scholar
Pilch, M. & Erdman, C.A. 1987 Use of breakup time data and velocity history data to predict the maximum size of stable fragments for acceleration-induced breakup of a liquid drop. Intl J. Multiphase Flow 13 (6), 741–757.CrossRefGoogle Scholar
Plümacher, D., Oberlack, M., Wang, Y. & Smuda, M. 2020 On a non-linear droplet oscillation theory via the unified method. Phys. Fluids 32 (6), 067104.CrossRefGoogle Scholar
Pope, S.B. 1988 The evolution of surface in turbulence. Intl J. Engng Sci. 26 (5), 445–469.CrossRefGoogle Scholar
Prosperetti, A. 1977 Viscous effects on perturbed spherical flows. Q. Appl. Maths 34 (4), 339–352.CrossRefGoogle Scholar
Providakis, T., Zimmer, L., Scouflaire, P., Ducruix, S. 2012 Characterization of the acoustic interactions in a two-stage multi-injection combustor fed with liquid fuel. Trans. ASME: J. Engng Gas Turbine. Power 134 (11), 111503.Google Scholar
Raviart, P.-A. & Sainsaulieu, L. 1995 A non-conservative hyperbolic system modeling spray dynamics. Part I. Solution of the Riemann problem. Math. Models Meth. Appl. Sci. 5 (3), 297–333.CrossRefGoogle Scholar
Rayleigh, Lord 1879 VI. On the capillary phenomena of jets. Proc. R. Soc. 29 (196-199), 71–97.Google Scholar
Sakano, Y., Nambu, T., Mizobuchi, Y. & Sato, T. 2022 Evaluation of three-dimensional droplet shape for analysis of the crossflow-type atomization. Mech. Engng J. 9 (1), 21-00378.Google Scholar
Salmon, R. 1983 Practical use of Hamilton's principle. J. Fluid Mech. 132, 431–444.CrossRefGoogle Scholar
Saurel, R., Chinnayya, A. & Carmouze, Q. 2017 Modelling compressible dense and dilute two-phase flows. Phys. Fluids 29 (6), 063301.CrossRefGoogle Scholar
Saurel, R., Gavrilyuk, S. & Renaud, F. 2003 A multiphase model with internal degrees of freedom: application to shock–bubble interaction. J. Fluid Mech. 495, 283–321.CrossRefGoogle Scholar
Scardovelli, R. & Zaleski, S. 1999 Direct numerical simulation of free-surface an interfacial flow. Annu. Rev. Fluid Mech. 31 (1), 567–603.CrossRefGoogle Scholar
Schmidmayer, K., Petitpas, F., Daniel, E., Favrie, N. & Gavrilyuk, S. 2017 A model and numerical method for compressible flows with capillary effects. J. Comput. Phys. 334, 468–496.CrossRefGoogle Scholar
Schmüdgen, K. 2017 The Moment Problem, Graduate Texts in Mathematics, vol. 277. Springer.CrossRefGoogle Scholar
Serre, D. 2010 The structure of dissipative viscous system of conservation laws. Physica D: Nonlinear Phenom. 239 (15), 1381–1386.CrossRefGoogle Scholar
Serrin, J. 1959 Mathematical principles of classical fluid mechanics. In Fluid Dynamics I/Strömungsmechanik I (ed. C. Truesdell), pp. 125–263. Springer.CrossRefGoogle Scholar
Shinjo, J. & Umemura, A. 2010 Simulation of liquid jet primary breakup: dynamics of ligament and droplet formation. Intl J. Multiphase Flow 36 (7), 513–532.CrossRefGoogle Scholar
Tomar, G., Fuster, D., Zaleski, S. & Popinet, S. 2010 Multiscale simulations of primary atomization. Comput. Fluids 39 (10), 1864–1874.CrossRefGoogle Scholar
Truskinovsky, L. 1991 Kinks versus shocks. In Shock Induced Transitions and Phase Structures in General Media (ed. R. Fosdick, J.E. Dunn & M. Slemrod), The IMA Volumes in Mathematics and its Applications, vol. 52. Springer.Google Scholar
Vallet, A. & Borghi, R. 1999 Modélisation eulerienne de l'atomisation d'un jet liquide. C. R. Acad. Sci. IIB 327 (10), 1015–1020.Google Scholar
Vié, A., Laurent, F. & Massot, M. 2013 Size-velocity correlations in high order moment methods for polydisperse evaporating sprays: modeling and numerical issues. J. Comput. Phys. 237, 177–210.CrossRefGoogle Scholar
Williams, F.A. 1958 Spray combustion and atomization. Phys. Fluids 1 (6), 6.CrossRefGoogle Scholar
Wolfram Research, Inc. 2023 Mathematica, Version 13.3.Google Scholar