Article contents
Small-scale dynamo action in rotating compressible convection
Published online by Cambridge University Press: 21 November 2011
Abstract
We study dynamo action in a convective layer of electrically conducting, compressible fluid, rotating about the vertical axis. At the upper and lower bounding surfaces, perfectly conducting boundary conditions are adopted for the magnetic field. Two different levels of thermal stratification are considered. If the magnetic diffusivity is sufficiently small, the convection acts as a small-scale dynamo. Using a definition for the magnetic Reynolds number 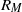 that is based upon the horizontal integral scale and the horizontally averaged velocity at the mid-layer of the domain, we find that rotation tends to reduce the critical value of
that is based upon the horizontal integral scale and the horizontally averaged velocity at the mid-layer of the domain, we find that rotation tends to reduce the critical value of 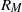 above which dynamo action is observed. Increasing the level of thermal stratification within the layer does not significantly alter the critical value of
above which dynamo action is observed. Increasing the level of thermal stratification within the layer does not significantly alter the critical value of 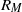 in the rotating calculations, but it does lead to a reduction in this critical value in the non-rotating cases. At the highest computationally accessible values of the magnetic Reynolds number, the saturation levels of the dynamo are similar in all cases, with the mean magnetic energy density somewhere between 4 and 9 % of the mean kinetic energy density. To gain further insights into the differences between rotating and non-rotating convection, we quantify the stretching properties of each flow by measuring Lyapunov exponents. Away from the boundaries, the rate of stretching due to the flow is much less dependent upon depth in the rotating cases than it is in the corresponding non-rotating calculations. It is also shown that the effects of rotation significantly reduce the magnetic energy dissipation in the lower part of the layer. We also investigate certain aspects of the saturation mechanism of the dynamo.
in the rotating calculations, but it does lead to a reduction in this critical value in the non-rotating cases. At the highest computationally accessible values of the magnetic Reynolds number, the saturation levels of the dynamo are similar in all cases, with the mean magnetic energy density somewhere between 4 and 9 % of the mean kinetic energy density. To gain further insights into the differences between rotating and non-rotating convection, we quantify the stretching properties of each flow by measuring Lyapunov exponents. Away from the boundaries, the rate of stretching due to the flow is much less dependent upon depth in the rotating cases than it is in the corresponding non-rotating calculations. It is also shown that the effects of rotation significantly reduce the magnetic energy dissipation in the lower part of the layer. We also investigate certain aspects of the saturation mechanism of the dynamo.
- Type
- Papers
- Information
- Copyright
- Copyright © Cambridge University Press 2011
References
- 19
- Cited by


