Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Deshpande, Rahul
Monty, Jason P.
and
Marusic, Ivan
2019.
Streamwise inclination angle of large wall-attached structures in turbulent boundary layers.
Journal of Fluid Mechanics,
Vol. 877,
Issue. ,
2020.
Characteristics of wall-attached motions in open channel flows.
Physics of Fluids,
Vol. 32,
Issue. 5,
p.
055110.
Ligęza, Paweł
2020.
Static and dynamic parameters of hot-wire sensors in a wide range of filament diameters as a criterion for optimal sensor selection in measurement process.
Measurement,
Vol. 151,
Issue. ,
p.
107177.
Cheng, Cheng
Li, Weipeng
Lozano-Durán, Adrián
Fan, Yitong
and
Liu, Hong
2020.
On the structure of streamwise wall-shear stress fluctuations in turbulent channel flows.
Journal of Physics: Conference Series,
Vol. 1522,
Issue. 1,
p.
012010.
Cheng, Cheng
Li, Weipeng
Lozano-Durán, Adrián
and
Liu, Hong
2020.
On the structure of streamwise wall-shear stress fluctuations in turbulent channel flows.
Journal of Fluid Mechanics,
Vol. 903,
Issue. ,
Chandran, Dileep
Monty, Jason P.
and
Marusic, Ivan
2020.
Spectral-scaling-based extension to the attached eddy model of wall turbulence.
Physical Review Fluids,
Vol. 5,
Issue. 10,
Samie, Milad
Lavoie, Philippe
and
Pollard, Andrew
2021.
Quantifying eddy structures and very-large-scale motions in turbulent round jets.
Journal of Fluid Mechanics,
Vol. 916,
Issue. ,
Birnir, Björn
Angheluta, Luiza
Kaminsky, John
and
Chen, Xi
2021.
Spectral link of the generalized Townsend-Perry constants in turbulent boundary layers.
Physical Review Research,
Vol. 3,
Issue. 4,
Li, Xuebo
Wang, Guohua
and
Zheng, Xiaojing
2021.
Logarithmic energy profile of the streamwise velocity for wall-attached eddies along the spanwise direction in turbulent boundary layer.
Physics of Fluids,
Vol. 33,
Issue. 10,
Deshpande, Rahul
de Silva, Charitha M.
Lee, Myoungkyu
Monty, Jason P.
and
Marusic, Ivan
2021.
Data-driven enhancement of coherent structure-based models for predicting instantaneous wall turbulence.
International Journal of Heat and Fluid Flow,
Vol. 92,
Issue. ,
p.
108879.
Hearst, R. Jason
de Silva, Charitha M.
Dogan, Eda
and
Ganapathisubramani, Bharathram
2021.
Uniform-momentum zones in a turbulent boundary layer subjected to freestream turbulence.
Journal of Fluid Mechanics,
Vol. 915,
Issue. ,
Zimmerman, Spencer
Klewicki, Joseph
and
Oberlack, Martin
2021.
Progress in Turbulence IX.
Vol. 267,
Issue. ,
p.
167.
Cheng, Cheng
Shyy, Wei
and
Fu, Lin
2022.
Streamwise inclination angle of wall-attached eddies in turbulent channel flows.
Journal of Fluid Mechanics,
Vol. 946,
Issue. ,
Chun, Sejong
2022.
Time-series analysis of differential pressure and flow velocity signals by means of weighted statistics.
Measurement,
Vol. 190,
Issue. ,
p.
110682.
Li, Xuebo
Wang, Guohua
and
Zheng, Xiaojing
2022.
Turbulent/Synoptic Separation and Coherent Structures in the Atmospheric Surface Layer for a Range of Surface Roughness.
Boundary-Layer Meteorology,
Vol. 182,
Issue. 1,
p.
75.
Li, Xuebo
Hutchins, Nicholas
Zheng, Xiaojing
Marusic, Ivan
and
Baars, Woutijn J.
2022.
Scale-dependent inclination angle of turbulent structures in stratified atmospheric surface layers.
Journal of Fluid Mechanics,
Vol. 942,
Issue. ,
Zheng, Xiaobo
Bellani, Gabriele
Mascotelli, Lucia
Örlü, Ramis
Ianiro, Andrea
Vila, Carlos Sanmiguel
Discetti, Stefano
Serpieri, Jacopo
Raiola, Marco
Talamelli, Alessandro
Li, Ye
and
Jiang, Nan
2022.
Inter-scale interaction in pipe flows at high Reynolds numbers.
Experimental Thermal and Fluid Science,
Vol. 131,
Issue. ,
p.
110529.
Wang, Longwei
Pan, Chong
Wang, Jinjun
and
Gao, Qi
2022.
Statistical signatures of component wall-attached eddies in proper orthogonal decomposition modes of a turbulent boundary layer.
Journal of Fluid Mechanics,
Vol. 944,
Issue. ,
Liu, Yixun
Liu, Chun-Ho
Brasseur, Guy P.
and
Chao, Christopher Y. H.
2023.
Amplitude modulation of velocity fluctuations in the atmospheric flows over real urban morphology.
Physics of Fluids,
Vol. 35,
Issue. 2,
Foroozan, F
Güemes, A
Raiola, M
Castellanos, R
Discetti, S
and
Ianiro, A
2023.
Synchronized measurement of instantaneous convective heat flux and velocity fields in wall-bounded flows.
Measurement Science and Technology,
Vol. 34,
Issue. 12,
p.
125301.
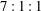 $7:1:1$ in the streamwise, spanwise and wall-normal directions, respectively.
$7:1:1$ in the streamwise, spanwise and wall-normal directions, respectively.

