Article contents
Simulations of rib-roughened rough-to-smooth turbulent channel flows
Published online by Cambridge University Press: 21 March 2018
Abstract
High-fidelity simulations of turbulent flow through a channel with a rough wall, followed by a smooth wall, demonstrate a high degree of non-equilibrium within the recovery region. In fact, the recovery of all the flow statistics studied is incomplete by the streamwise exit of the computational domain. Above a thin wall layer, turbulence intensities significantly higher than fully developed, smooth-wall levels persist in the developing region. Within the thin wall layer, the profile shapes for turbulence stresses recover very quickly and wall-normal locations of characteristic peaks are established. However, even in this thin layer, complete recovery of magnitudes of turbulence stresses is exceptionally slow. A similar initially swift but eventually incomplete and slow relaxation behaviour is also shown by the skin friction. Between the turbulence shear and streamwise stresses, the turbulence shear stress shows a comparatively quick rate of recovery above a thin wall layer. Over the developing smooth wall, the balance is not merely between fluxes due to pressure and shear stresses. Strong momentum fluxes, which are directly influenced by the upstream roughness size, contribute significantly to this balance. Approximate curve fits estimate the streamwise distance required by the outer peaks of Reynolds stresses to attain near-fully-developed levels at approximately 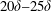 $20\unicode[STIX]{x1D6FF}{-}25\unicode[STIX]{x1D6FF}$, with
$20\unicode[STIX]{x1D6FF}{-}25\unicode[STIX]{x1D6FF}$, with 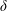 $\unicode[STIX]{x1D6FF}$ being the channel half height. An even longer distance, of more than
$\unicode[STIX]{x1D6FF}$ being the channel half height. An even longer distance, of more than 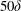 $50\unicode[STIX]{x1D6FF}$, might be needed by the mean velocity to approach near-fully-developed magnitudes. Visualizations and correlations show that large-scale eddies that are created above the roughness persist downstream, and sporadically perturb the elongated streaks. These streaks of alternating high and low momentum appear almost instantly after the roughness is removed. The mean flow does not re-establish an equilibrium log layer within the computational domain, and the velocity deficit created by the roughness continues throughout the domain. On the step change in roughness, near the wall, profiles for turbulence kinetic energy dissipation rate,
$50\unicode[STIX]{x1D6FF}$, might be needed by the mean velocity to approach near-fully-developed magnitudes. Visualizations and correlations show that large-scale eddies that are created above the roughness persist downstream, and sporadically perturb the elongated streaks. These streaks of alternating high and low momentum appear almost instantly after the roughness is removed. The mean flow does not re-establish an equilibrium log layer within the computational domain, and the velocity deficit created by the roughness continues throughout the domain. On the step change in roughness, near the wall, profiles for turbulence kinetic energy dissipation rate,  $\unicode[STIX]{x1D716}$, and energy spectra indicate a sharp reduction in energy at small scales. Despite this, reversion towards equilibrium smooth-wall levels is slow, and ultimately incomplete, due to a rather slow adjustment of the turbulence cascade. The non-dimensional roughness height,
$\unicode[STIX]{x1D716}$, and energy spectra indicate a sharp reduction in energy at small scales. Despite this, reversion towards equilibrium smooth-wall levels is slow, and ultimately incomplete, due to a rather slow adjustment of the turbulence cascade. The non-dimensional roughness height, 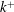 $k^{+}$ ranges from 42 to 254 and the friction velocity Reynolds number at the smooth wall,
$k^{+}$ ranges from 42 to 254 and the friction velocity Reynolds number at the smooth wall, 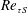 $Re_{\unicode[STIX]{x1D70F}S}$, ranges from 284 to 1160 in the various simulations.
$Re_{\unicode[STIX]{x1D70F}S}$, ranges from 284 to 1160 in the various simulations.
JFM classification
- Type
- JFM Papers
- Information
- Copyright
- © 2018 Cambridge University Press
References
- 37
- Cited by


