Published online by Cambridge University Press: 05 May 2017
Orderly, or natural, transition to turbulence in dilute polymeric channel flow is studied using direct numerical simulations of a FENE-P fluid. Three Weissenberg numbers are simulated and contrasted to a reference Newtonian configuration. The computations start from infinitesimally small Tollmien–Schlichting (TS) waves and track the development of the instability from the early linear stages through nonlinear amplification, secondary instability and full breakdown to turbulence. At the lowest elasticity, the primary TS wave is more unstable than the Newtonian counterpart, and its secondary instability involves the generation of 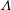 $\unicode[STIX]{x1D6EC}$-structures which are narrower in the span. These subsequently lead to the formation of hairpin packets and ultimately breakdown to turbulence. Despite the destabilizing influence of weak elasticity, and the resulting early transition to turbulence, the final state is a drag-reduced turbulent flow. At the intermediate elasticity, the growth rate of the primary TS wave matches the Newtonian value. However, unlike the Newtonian instability mode which reaches a saturated equilibrium condition, the instability in the polymeric flow reaches a periodic state where its energy undergoes cyclical amplification and decay. The spanwise size of the secondary instability in this case is commensurate with the Newtonian
$\unicode[STIX]{x1D6EC}$-structures which are narrower in the span. These subsequently lead to the formation of hairpin packets and ultimately breakdown to turbulence. Despite the destabilizing influence of weak elasticity, and the resulting early transition to turbulence, the final state is a drag-reduced turbulent flow. At the intermediate elasticity, the growth rate of the primary TS wave matches the Newtonian value. However, unlike the Newtonian instability mode which reaches a saturated equilibrium condition, the instability in the polymeric flow reaches a periodic state where its energy undergoes cyclical amplification and decay. The spanwise size of the secondary instability in this case is commensurate with the Newtonian 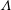 $\unicode[STIX]{x1D6EC}$-structures, and the extent of drag reduction in the final turbulent state is enhanced relative to the lower elasticity condition. At the highest elasticity, the exponential growth rate of the TS wave is weaker than the Newtonian flow and, as a result, the early linear stage is prolonged. In addition, the magnitude of the saturated TS wave is appreciably lower than the other conditions. The secondary instability is also much wider in the span, with weaker ejection and without hairpin packets. Instead, streamwise-elongated streaks are formed and break down to turbulence via secondary instability. The final state is a high-drag-reduction flow, which approaches the Virk asymptote.
$\unicode[STIX]{x1D6EC}$-structures, and the extent of drag reduction in the final turbulent state is enhanced relative to the lower elasticity condition. At the highest elasticity, the exponential growth rate of the TS wave is weaker than the Newtonian flow and, as a result, the early linear stage is prolonged. In addition, the magnitude of the saturated TS wave is appreciably lower than the other conditions. The secondary instability is also much wider in the span, with weaker ejection and without hairpin packets. Instead, streamwise-elongated streaks are formed and break down to turbulence via secondary instability. The final state is a high-drag-reduction flow, which approaches the Virk asymptote.