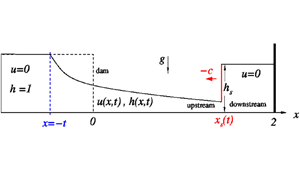
We revisit the theoretical solutions of the problem of the reflected flow from a vertical obstacle encountered by a current generated by dambreak of a Cartesian long reservoir over a dry bottom and with tailwaters. Previous investigations derived accurate solutions by quite complex manipulation of the balances along the characteristics, supported by numerical solutions, of the shallow-water equations (a significant extension is the recent paper Hogg & Skevington, Q. J. Mech. Appl. Maths, vol. 74, no. 4, 2021, pp. 441–465). Here we developed a simplified model, based on the major assumption that the fluid between the obstacle (wall) and the reflected jump is stagnant. This allows the solution of the problem by a straightforward numerical integration of one initial-value ordinary differential equation. The model provides the position, height and speed of the jump as functions of time. For long times a simple analytical approximation is also available. The model points out clear-cut effects of the presence of the tailwaters. The model has been validated by comparisons with exact solutions of the shallow-water equations of the recent study of Hogg & Skevington (Q. J. Mech. Appl. Maths, vol. 74, no. 4, 2021, pp. 441–465) (obtained by significantly more complex hodograph-plane methods). In all the tested cases the agreement is good, for long periods of time. This model provides reliable insights and fast quantitative predictions recommended for use in research and engineering problems where a fair approximation is sufficient for the application.