Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Denn, Morton M.
1967.
Boundary layer flows for a class of elastic fluids.
Chemical Engineering Science,
Vol. 22,
Issue. 3,
p.
395.
Hsu, Chen‐Chi
1969.
A simple solution for boundary layer flow of power law fluids past a semi‐infinite flat plate.
AIChE Journal,
Vol. 15,
Issue. 3,
p.
367.
Balmer, R. T.
and
Kauzlaich, James J.
1971.
Similarity solutions for the converging or diverging steady flow of non‐newtonian elastic power law fluids with wall suction or injection. Part I: Two‐dimensional channel flow.
AIChE Journal,
Vol. 17,
Issue. 5,
p.
1181.
Nath, Grishwar
1974.
An Approximate Method for the Similar Solution of Nonlinear Boundary Layer Equations for Power‐Law Fluids.
ZAMM - Journal of Applied Mathematics and Mechanics / Zeitschrift für Angewandte Mathematik und Mechanik,
Vol. 54,
Issue. 3,
p.
198.
Chen, J.L.S.
1986.
Similar steady and unsteady flows of inelastic fluid over axisymmetric bodies.
International Journal of Engineering Science,
Vol. 24,
Issue. 7,
p.
1075.
Filip, P.
Kolář, V.
and
Hájek, R.
1991.
Similarity prediction of wall jets past axisymmetric bodies for power-law fluids.
Acta Mechanica,
Vol. 88,
Issue. 3-4,
p.
167.
1993.
Fluid Mechanics for Petroleum Engineers.
Vol. 32,
Issue. ,
p.
389.
Na, T.Y.
1994.
Boundary layer flow of Reiner-Philippoff fluids.
International Journal of Non-Linear Mechanics,
Vol. 29,
Issue. 6,
p.
871.
Yürüsoy, Muhammet
and
Pakdemirli, Mehmet
1997.
Symmetry reductions of unsteady three-dimensional boundary layers of some non-Newtonian fluids.
International Journal of Engineering Science,
Vol. 35,
Issue. 8,
p.
731.
Yürüsoy, Muhammet
2006.
Unsteady boundary layer flow of power-law fluid on stretching sheet surface.
International Journal of Engineering Science,
Vol. 44,
Issue. 5-6,
p.
325.
Kolář, Václav
2011.
Similarity solution of axisymmetric non-Newtonian wall jets with swirl.
Nonlinear Analysis: Real World Applications,
Vol. 12,
Issue. 6,
p.
3413.
Madani Tonekaboni, Seyed Ali
Abkar, Ramin
Khoeilar, Reza
and
Milovanović, Gradimir V.
2012.
On the Study of Viscoelastic Walters′ B Fluid in Boundary Layer Flows.
Mathematical Problems in Engineering,
Vol. 2012,
Issue. 1,
Patil, Vishwambhar S.
Patil, Nalini S.
and
Timol, M.G.
2015.
A remark on similarity analysis of boundary layer equations of a class of non-Newtonian fluids.
International Journal of Non-Linear Mechanics,
Vol. 71,
Issue. ,
p.
127.
Mahapatra, T.R.
and
Sidui, S.
2020.
Non-axisymmetric Homann stagnation-point flow of a viscoelastic fluid towards a fixed plate.
European Journal of Mechanics - B/Fluids,
Vol. 79,
Issue. ,
p.
38.
Shah, Babar Hussain
and
Tang, Zhili
2025.
Fluids dynamics of non-Newtonian power-law fluids: Investigating separation points on cylindrical shapes.
Physics of Fluids,
Vol. 37,
Issue. 3,
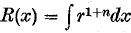 for axisymmetric flows, r is the distance from the axis to the wall, and A, B, d, m are constants.
for axisymmetric flows, r is the distance from the axis to the wall, and A, B, d, m are constants.