Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-03T02:19:36.541Z Has data issue: false hasContentIssue false
  • English
  • Français

Similarity and structure of wall turbulence with lateral wall shear stress variations

Published online by Cambridge University Press:  23 May 2018

D. Chung Open the ORCID record for D. Chung [Opens in a new window] ,
J. P. Monty  and
N. Hutchins
D. Chung*
Affiliation:
Department of Mechanical Engineering, University of Melbourne, Victoria 3010, Australia
J. P. Monty
Affiliation:
Department of Mechanical Engineering, University of Melbourne, Victoria 3010, Australia
N. Hutchins
Affiliation:
Department of Mechanical Engineering, University of Melbourne, Victoria 3010, Australia
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Wall-bounded turbulence, where it occurs in engineering or nature, is commonly subjected to spatial variations in wall shear stress. A prime example is spatially varying roughness. Here, we investigate the configuration where the wall shear stress varies only in the lateral direction. The investigation is idealised in order to focus on one aspect, namely, the similarity and structure of turbulent inertial motion over an imposed scale of stress variation. To this end, we analyse data from direct numerical simulation (DNS) of pressure-driven turbulent flow through a channel bounded by walls of laterally alternating patches of high and low wall shear stress. The wall shear stress is imposed as a Neumann boundary condition such that the wall shear stress ratio is fixed at 3 while the lateral spacing $s$ of the uniform-stress patches is varied from 0.39 to 6.28 of the half-channel height 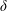$\unicode[STIX]{x1D6FF}$. We find that global outer-layer similarity is maintained when $s$ is less than approximately 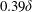$0.39\unicode[STIX]{x1D6FF}$ while local outer-layer similarity is recovered when $s$ is greater than approximately 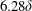$6.28\unicode[STIX]{x1D6FF}$. However, the transition between the two regimes through 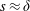$s\approx \unicode[STIX]{x1D6FF}$ is not monotonic owing to the presence of secondary roll motions that extend across the whole cross-section of the flow. Importantly, these secondary roll motions are associated with an amplified skin-friction coefficient relative to both the small- and large-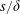$s/\unicode[STIX]{x1D6FF}$ limits. It is found that the relationship between the secondary roll motions and the mean isovels is reversed through this transition from low longitudinal velocity over low stress at small 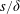$s/\unicode[STIX]{x1D6FF}$ to high longitudinal velocity over low stress at large 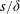$s/\unicode[STIX]{x1D6FF}$.

JFM classification

Turbulent Flows: Turbulent boundary layers Turbulent Flows: Turbulent Flows Turbulent Flows: Turbulence simulation
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 847 , 25 July 2018 , pp. 591 - 613
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

del Álamo, J. C. & Jiménez, J. 2006 Linear energy amplification in turbulent channels. J. Fluid Mech. 559, 205–213.Google Scholar
Anderson, W., Barros, J. M., Christensen, K. T. & Awasthi, A. 2015 Numerical and experimental study of mechanisms responsible for turbulent secondary flows in boundary layer flows over spanwise heterogeneous roughness. J. Fluid Mech. 768, 316–347.CrossRefGoogle Scholar
Antonia, R. A. & Luxton, R. E. 1971 The response of a turbulent boundary layer to a step change in surface roughness. Part 1. Smooth to rough. J. Fluid Mech. 48, 721–761.Google Scholar
Antonia, R. A. & Luxton, R. E. 1972 The response of a turbulent boundary layer to a step change in surface roughness. Part 2. Rough-to-smooth. J. Fluid Mech. 53, 737–757.Google Scholar
Barros, J. M. & Christensen, K. T. 2014 Observations of turbulent secondary flows in a rough-wall boundary layer. J. Fluid Mech. 748, R1.CrossRefGoogle Scholar
Bernardini, M., Pirozzoli, S., Quadrio, M. & Orlandi, P. 2013 Turbulent channel flow simulations in a convecting reference frames. J. Comput. Phys. 232, 1–6.Google Scholar
Bou-Zeid, E., Meneveau, C. & Parlange, M. B. 2004 Large-eddy simulation of neutral atmospheric boundary layer flow over heterogeneous surfaces: blending height and effective surface roughness. Water Resour. Res. 40, W02505.Google Scholar
Bou-Zeid, E., Parlange, M. B. & Meneveau, C. 2007 On the parameterization of surface roughness at regional scales. J. Atmos. Sci. 64, 216–227.CrossRefGoogle Scholar
Bradshaw, P. 1987 Turbulent secondary flows. Annu. Rev. Fluid Mech. 19, 53–74.Google Scholar
Chung, D., Monty, J. P. & Ooi, A. 2014 An idealised assessment of Townsend’s outer-layer similarity hypothesis for wall turbulence. J. Fluid Mech. 742, R3.Google Scholar
Flack, K. A. & Schultz, M. P. 2014 Roughness effects on wall-bounded turbulent flows. Phys. Fluids 26, 101305.Google Scholar
Flack, K. A., Schultz, M. P. & Connelly, J. S. 2007 Examination of a critical roughness height for outer layer similarity. Phys. Fluids 19, 095104.Google Scholar
Goldstein, D. B. & Tuan, T.-C. 1998 Secondary flow induced by riblets. J. Fluid Mech. 363, 115–151.Google Scholar
Hanson, R. E. & Ganapathisubramani, B. 2016 Development of turbulent boundary layers past a step change in wall roughness. J. Fluid Mech. 795, 494–523.Google Scholar
Hinze, J. O. 1967 Secondary currents in wall turbulence. Phys. Fluids 10, S122–S125.Google Scholar
Hinze, J. O. 1973 Experimental investigation on secondary currents in the turbulent flow through a straight conduit. Appl. Sci. Res. 28, 453–465.Google Scholar
Hutchins, N., Monty, J. P., Ganapathisubramani, B., Ng, H. C. H. & Marusic, I. 2011 Three-dimensional conditional structure of a high-Reynolds-number turbulent boundary layer. J. Fluid Mech. 673, 255–285.CrossRefGoogle Scholar
Hwang, Y. & Cossu, C. 2010 Linear non-normal energy amplification of harmonic and stochastic forcing in turbulent channel flow. J. Fluid Mech. 664, 51–73.Google Scholar
Jelly, T. O., Jung, S. Y. & Zaki, T. A. 2014 Turbulence and skin friction modification in channel flow with streamwise-aligned superhydrophobic surface texture. Phys. Fluids 26, 095102.CrossRefGoogle Scholar
Jiménez, J. 2004 Turbulent flows over rough walls. Annu. Rev. Fluid Mech. 36, 173–196.CrossRefGoogle Scholar
Kozul, M., Chung, D. & Monty, J. P. 2016 Direct numerical simulation of the incompressible temporally developing turbulent boundary layer. J. Fluid Mech. 796, 437–472.Google Scholar
Lozano-Durán, A. & Jiménez, J. 2014 Effect of computational domain on direct simulations of turbulent channels up to Re 𝜏 = 4200. Phys. Fluids 26, 011702.CrossRefGoogle Scholar
Mason, P. J. 1988 The formation of areally-averaged roughness lengths. Q. J. R. Meteorol. Soc. 114, 399–420.Google Scholar
Medjnoun, T., Vanderwel, C. & Ganapathisubramani, B. 2018 Characteristics of turbulent boundary layers over smooth surfaces with spanwise heterogeneities. J. Fluid Mech. 838, 516–543.Google Scholar
Mehta, R. D. & Bradshaw, P. 1988 Longitudinal vortices imbedded in turbulent boundary layers. Part 2. Vortex pair with ‘common flow’ upwards. J. Fluid Mech. 188, 529–546.CrossRefGoogle Scholar
Moody, L. F. 1944 Friction factors for pipe flow. Trans. ASME 66, 671–684.Google Scholar
Moser, R. D., Kim, J. & Mansour, N. N. 1999 Direct numerical simulation of turbulent channel flow up to Re 𝜏 = 590. Phys. Fluids 11, 943–945.Google Scholar
Nugroho, B., Hutchins, N. & Monty, J. P. 2013 Large-scale spanwise periodicity in a turbulent boundary layer induced by highly ordered and directional surface roughness. Intl J. Heat Fluid Flow 41, 90–102.Google Scholar
Perot, J. B. 1993 An analysis of the fractional step method. J. Comput. Phys. 108, 51–58.Google Scholar
Raupach, M. R., Antonia, R. A. & Rajagopalan, S. 1991 Rough-wall turbulent boundary layers. Appl. Mech. Rev. 44, 1–25.Google Scholar
Saito, N. & Pullin, D. I. 2014 Large eddy simulation of smooth-rough-smooth transitions in turbulent channel flows. Intl J. Heat Mass Transfer. 78, 707–720.Google Scholar
Sanderse, B., Verstappen, R. W. C. P. & Koren, B. 2014 Boundary treatment for fourth-order staggered mesh discretizations of the incompressible Navier–Stokes equations. J. Comput. Phys. 257, 1472–1505.Google Scholar
Spalart, P. R. & McLean, J. D. 2011 Drag reduction: enticing turbulence, and then an industry. Phil. Trans. R. Soc. Lond. A 369, 1556–1569.Google Scholar
Spalart, P. R., Moser, R. D. & Rogers, M. M. 1991 Spectral methods for the Navier–Stokes equations with one infinite and two periodic directions. J. Comput. Phys. 96, 297–324.Google Scholar
Tennekes, H. & Lumley, J. L. 1972 A First Course in Turbulence. MIT.Google Scholar
Townsend, A. A. 1976 The Structure of Turbulent Shear Flow, 2nd edn. Cambridge University Press.Google Scholar
Vanderwel, C. & Ganapathisubramani, B. 2015 Effects of spanwise spacing on large-scale secondary flows in rough-wall turbulent boundary layers. J. Fluid Mech. 774, R2.Google Scholar
Verstappen, R. W. C. P. & Veldman, A. E. P. 2003 Symmetry-preserving discretization of turbulent flow. J. Comput. Phys. 187, 343–368.Google Scholar
Willingham, D., Anderson, W., Christensen, K. T. & Barros, J. M. 2014 Turbulent boundary layer flow over transverse aerodynamic roughness transitions: induced mixing and flow characterization. Phys. Fluids 26, 025111.Google Scholar